|
IMC '05 Paper
[IMC '05 Technical Program]


Improving Sketch Reconstruction Accuracy
Using Linear Least Squares Method
Gene Moo Lee, Huiya Liu, Young Yoon and Yin Zhang
Department of Computer Sciences
University of Texas at Austin
Austin, TX 78712, USA
{gene,huiyaliu,agitato7,yzhang}@cs.utexas.edu
Abstract:
Sketch is a sublinear space data structure that allows one to
approximately reconstruct the value associated with any given key in
an input data stream. It is the basis for answering a number of
fundamental queries on data streams, such as range queries, finding
quantiles, frequent items, etc. In the networking context, sketch has
been applied to identifying heavy hitters and changes, which is
critical for traffic monitoring, accounting, and network anomaly
detection.
In this paper, we propose a novel approach called lsquare to
significantly improve the reconstruction accuracy of the sketch data
structure. Given a sketch and a set of keys, we estimate the values
associated with these keys by constructing a linear system and finding
the optimal solution for the system using linear least squares method.
We use a large amount of real Internet traffic data to evaluate
lsquare against countmin, the state-of-the-art sketch
scheme. Our results suggest that given the same memory requirement,
lsquare achieves much better reconstruction accuracy than
countmin. Alternatively, given the same reconstruction
accuracy, lsquare requires significantly less memory. This
clearly demonstrates the effectiveness of our approach.
1 Introduction
For many network management applications, it is essential to
accurately monitor and analyze network traffic. For example, Internet
service providers need to monitor the usage information in order to
support usage-based pricing. Network operators need to observe the
traffic pattern to perform traffic engineering. Network anomaly
detection systems need to continuously monitor the traffic in order to
uncover anomalous traffic patterns in near real-time, especially those
caused by flash crowds, denial-of-service attacks (DoS), worms, and
network element failures. These applications typically treat the
traffic as a collection of flows with some properties to keep
track of (e.g., volume, number of packets). The flows are typically
identified by certain combination of packet header fields (e.g., IP
addresses, port numbers, and protocol).
A naïve approach for network traffic measurement is to maintain
state and perform analysis on a per-flow basis. However, as
link speeds and the number of flows increase, keeping per-flow state
can quickly become either too expensive or too slow. As a result, a
lot of recent networking research efforts have been directed towards
developing scalable and accurate techniques for performing traffic
monitoring and analysis without keeping per-flow state
(e.g., [6]). Meanwhile, computation over massive
data streams has been an active research area in the database research
community over the past several years. The emerging field of data stream computation deals with various aspects of computation
that can be performed in a space- and time-efficient manner when each
item in a data stream can be accessed only once (or a small number of
times). A rich body of algorithms and techniques have been developed.
A good survey of the algorithms and applications in data stream
computation can be found in [11].
A particularly powerful technique is sketch [1,7,3,5], a probabilistic summary
data structure proposed for analyzing massive data streams. Sketches
avoid keeping per-flow state by dimensionality reduction techniques,
using projections along random vectors. Sketches have some
interesting properties that have proven to be very useful in analyzing
data streams: they are space efficient, provide provable probabilistic
reconstruction accuracy guarantees, and are linear (i.e., sketches can
be combined in an arithmetical sense). These properties have made
sketch the basis for answering a number of fundamental queries on data
streams, such as range queries, finding quantiles and frequent items
[11]. In the networking context, sketch has been
successfully applied to detecting heavy hitters and changes
[8,4].
A key operation on the sketch data structure is so called point
estimation, i.e., to estimate the accumulated value associated with a
given key. All existing methods perform point estimation for
different keys separately and only have limited accuracy. In this
paper, we propose a novel method called lsquare to
significantly improve the accuracy of point estimation on the sketch
data structure. Instead of estimating values for individual keys
separately, lsquare first extracts a set of keys that is a
superset of all the heavy hitter flows and then simultaneously
estimates the accumulated values for this set of keys - it does so by
first constructing a linear system and then finding the optimal
solution to the system through linear least squares method.
We use a large amount of real Internet traffic data to evaluate our
method against countmin [5], the best
existing sketch scheme. Our results are encouraging: Given the same
memory requirement, lsquare yields much more accurate estimates
than countmin; and given the same reconstruction accuracy,
lsquare uses significantly less memory.
The remainder of the paper is organized as follows. In
Section 2, we give an overview of sketch data
structure, define the problem, and survey the related work. In
Section 3, we describe our lsquare method for
point estimation on the sketch data structure. In
Section 4, we evaluate the proposed method using
real Internet traffic data. We conclude in
Section 5.
2 Background
This section provides some background on the problem we want to solve.
First, we briefly describe the underlying data stream model and the
sketch data structure. Then we define the problem of point estimation
on sketch and explain the existing methods to solve the problem. We
will also briefly survey the related work.
Let
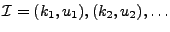 be an input stream
that arrives sequentially, item by item. Here be an input stream
that arrives sequentially, item by item. Here
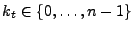 is a key and is a key and 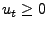 is the update value associated with
the key. Let is the update value associated with
the key. Let 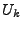 be the sum of update values for a key be the sum of update values for a key 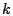 .
Here, the update values are non-negative, meaning that .
Here, the update values are non-negative, meaning that 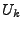 always
increase. This model is called the cash register model
[11]. Many applications of sketches guarantee that
counts are non-negative. However, we note that our proposed method is
also applicable to the more general Turnstile model
[11], in which update values may be negative. always
increase. This model is called the cash register model
[11]. Many applications of sketches guarantee that
counts are non-negative. However, we note that our proposed method is
also applicable to the more general Turnstile model
[11], in which update values may be negative.
Sketch [5,8,14] is a sublinear space data structure for
summarizing massive data streams. We use the notations in
Table 1 to specify the sketch data structure.
Data structure:
A sketch is a two-dimensional count array ![$ T[i][j]$](img16.gif) ( (
 ), where ), where 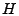 is the number of one-dimensional arrays
and is the number of one-dimensional arrays
and 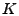 is the number of counts in each array. Each count of sketch
is initially set to zero. For each one-dimensional array is the number of counts in each array. Each count of sketch
is initially set to zero. For each one-dimensional array
![$ T[i][\cdot]$](img20.gif) , there is a hash function , there is a hash function
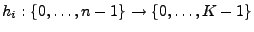 , where , where 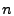 is the size of the key space. The hash
functions are chosen uniformly at random to be pair-wise
independent. We can view the data structure as an array of hash
tables. is the size of the key space. The hash
functions are chosen uniformly at random to be pair-wise
independent. We can view the data structure as an array of hash
tables.
Update procedure:
When an update
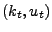 arrives, the update value arrives, the update value 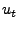 is added
to the corresponding count is added
to the corresponding count
![$ T[i][h_i(k_t)]$](img25.gif) in each hash table in each hash table 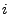 . .
Heavy hitter identification:
Since the sketch data structure only records the values, not the keys,
it is a challenge to identify the heavy-valued keys among all the keys
hashed into the heavy buckets. In order to identify heavy hitters, we
can keep a priority queue to record the top hitters with values above
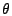 (as shown in [5]). An alternative is to
perform intersections among buckets with heavy counts, which is
proposed by Schweller et al. [14]. (as shown in [5]). An alternative is to
perform intersections among buckets with heavy counts, which is
proposed by Schweller et al. [14].
Point estimation:
Let 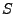 be a sketch and be a sketch and 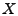 be a set of keys, which are known to be
heavy hitters. The problem of point estimation is to estimate
the total update value be a set of keys, which are known to be
heavy hitters. The problem of point estimation is to estimate
the total update value 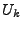 for any key for any key 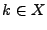 . This problem is
the focus of our paper. . This problem is
the focus of our paper.
Count-Min:
As proposed in [5], countmin is an existing
method to reconstruct the value for any given key. The minimum value
among all counts corresponding to the key is taken as an estimate of
the value. Formally,
is an estimate for the value 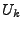 . Cormode and Muthukrishnan
[5] proved that . Cormode and Muthukrishnan
[5] proved that
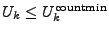 and that and that
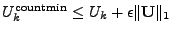 with probability with probability 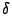 , where , where
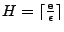 , ,
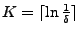 , and , and
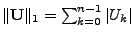 . In other words, countmin always overestimates with a
certain error bound. . In other words, countmin always overestimates with a
certain error bound.
Common applications of sketches include detecting heavy-hitters,
finding quantiles, answering range/point queries and estimating flow
size distribution [11].
Kumar et al. [9] used Expectation Maximization method to
infer the flow size distribution from an array of counters, which can
be viewed as a special case of sketch ( ). ).
Estan and Varghese [6] suggested an improved
sampling method called sample-and-hold, with which flow amount
is recorded only after individual entry for the flow is made.
They also proposed multi-stage filters for data summary, which
has the same data structure as sketch but uses a different update method
called conservative update. When an update arrives, only the
minimum valued bucket is incremented, whereas sketch increments
counters of 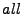 corresponding buckets. The minimum counter of
multi-stage filter can be used for point estimation, which is similar
to the countmin approach. corresponding buckets. The minimum counter of
multi-stage filter can be used for point estimation, which is similar
to the countmin approach.
Krishnamurthy et al. [8] proposed another point
estimation method for sketch, which can be used in the Turnstile data
stream model. The estimation
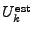 for a key for a key 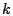 is
given as is
given as
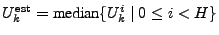 , where , where
![$ U_k^{i} = \frac{T[i][h_i(k)] - SUM/K}{1 - 1/K}$](img46.gif) and and
![$ SUM = \sum_{j=0}^{K-1} T[0][j]$](img47.gif) . .
3 Our Approach
In this section, we explain the proposed lsquare method for
point estimation. First, lsquare records the data flow
information in a sketch. Then it constructs a linear system based on
the sketch, and solves the system using linear least squares method.
Below we first give a simple example and then formally describe the
method.
Suppose we have a data stream from 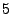 IP addresses. Let IP addresses. Let
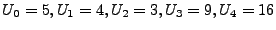 be the total amount of traffic
for each IP. We record the flows into a sketch with be the total amount of traffic
for each IP. We record the flows into a sketch with 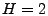 and and 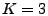 ,
which has two hash functions ,
which has two hash functions
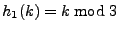 and and
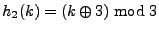 , where , where 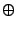 denotes bitwise-XOR. The sketch is
given as: denotes bitwise-XOR. The sketch is
given as:
Here, 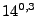 means that means that 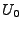 and and 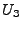 are hashed into the
bucket, resulting in a count of are hashed into the
bucket, resulting in a count of 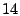 . The goal is to reconstruct . The goal is to reconstruct
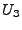 and and 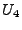 from the sketch. from the sketch.
Solution using countmin:
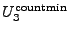 = min{ = min{![$ T[0][0]$](img63.gif) , , ![$ T[1][0]$](img64.gif) } = 14 and } = 14 and
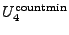 = min{ = min{![$ T[0][1]$](img66.gif) , , ![$ T[1][1]$](img67.gif) } = 19. } = 19.
Solution using lsquare:
First, we construct a linear system
 with
the constructed sketch. Vectors with
the constructed sketch. Vectors
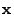 , ,
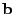 and matrix and matrix
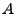 are specified as follows. are specified as follows.
Here, 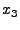 and and 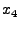 are variables for keys are variables for keys  and and 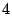 , and , and 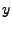 is
used to capture noise caused by keys that are not of our interest.
Matrix is
used to capture noise caused by keys that are not of our interest.
Matrix 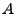 indicates which keys are hashed to which buckets, and
vector indicates which keys are hashed to which buckets, and
vector
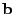 consists of values of all buckets. For example,
we have the equation consists of values of all buckets. For example,
we have the equation
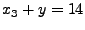 with bucket with bucket ![$ T[0][0]$](img63.gif) , which
corresponds to the first rows of , which
corresponds to the first rows of 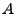 and and
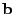 . .
With the constructed linear system, we find the optimal solution of
the linear system using linear least squares method:
![$ \mathbf{x} =
[10.5, 16.0, 3.5]^T$](img79.gif) (i.e., (i.e.,
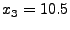 , ,
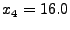 , , 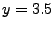 ). In
this simple example, our method clearly produces much more accurate
estimates than countmin. ). In
this simple example, our method clearly produces much more accurate
estimates than countmin.
Let 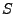 be a sketch and be a sketch and
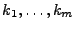 be the set of keys of our
interest. Then we have an unknown variables vector be the set of keys of our
interest. Then we have an unknown variables vector
![$ \mathbf{x} \in
\mathbb{R}^{(m+1) \times 1} = [x_{1}, \ldots, x_{m}, y]^T$](img84.gif) , where , where
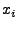 is for the value of key is for the value of key 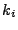 and and 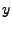 is an additional variable
for noise caused by keys not in is an additional variable
for noise caused by keys not in 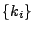 , which is
uniformly distributed over all buckets. We construct a matrix , which is
uniformly distributed over all buckets. We construct a matrix
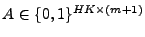 , showing which keys are hashed into
which buckets, and a vector , showing which keys are hashed into
which buckets, and a vector
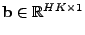 , containing values of every buckets. The elements of , containing values of every buckets. The elements of 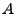 and and
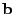 are specified as follows. For are specified as follows. For
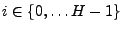 and and
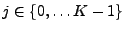 , ,
In general 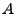 is not a square matrix and may be rank deficient. In
this case, a standard solution to is not a square matrix and may be rank deficient. In
this case, a standard solution to
 is the
pseudoinverse solution is the
pseudoinverse solution
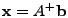 , where , where 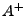 is
the pseudoinverse (i.e., Moore-Penrose inverse [10,13]) of matrix is
the pseudoinverse (i.e., Moore-Penrose inverse [10,13]) of matrix 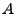 . It is known that . It is known that
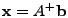 provides the shortest length least squares solution to the
system of linear equations provides the shortest length least squares solution to the
system of linear equations
 . More precisely,
it solves: . More precisely,
it solves:
where
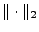 is the Euclidean norm. is the Euclidean norm.
Under the cash register data stream model, we can further improve the
estimation accuracy by incorporating lower-bound and upper-bound
constraints into the system. Specifically, we can use 0 as a lower
bound for
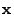 and the countmin estimation as an upper
bound. The pseudo-code for the resulting algorithm is given as follows. and the countmin estimation as an upper
bound. The pseudo-code for the resulting algorithm is given as follows.
vector lsquare(matrix A, vector b,
vector countmin)
{
x = pinv(A)*b; // pseudoinverse
x = max(x,0); // non-negativity
x = min(x,countmin); // upper bound: countmin
return x;
}
Note that so far we use a single variable 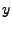 to capture the effects
of background noise. This assumes that we do not know any keys other
than those of our direct interest. In case we do know extra keys, we
can add them to to capture the effects
of background noise. This assumes that we do not know any keys other
than those of our direct interest. In case we do know extra keys, we
can add them to 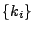 and treat the corresponding and treat the corresponding 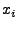 as
additional noise variables. We will show in
Section 4.3 that the use of additional noise
variables significantly improves the accuracy of lsquare. as
additional noise variables. We will show in
Section 4.3 that the use of additional noise
variables significantly improves the accuracy of lsquare.
4 Evaluation
In this section we evaluate our lsquare method on two Internet
trace data sets. Our results suggest that lsquare generally
produces more accurate estimates than countmin. Even better
accuracy can be achieved through the use of additional noise
variables. In addition, the accuracy of lsquare degrades
gracefully when less memory is available.
The Internet traffic data used in our evaluation is collected by
National Laboratory for Applied Network Research (NLANR) [12].
We choose two sets of data: BELL-02 [2] and TERA-04
[15]. Brief information of the data sets is given in
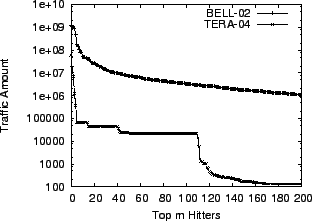
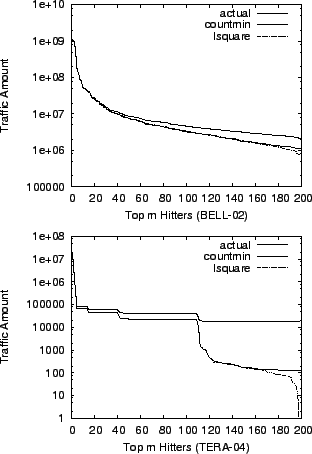
Table 2. Figure 1 shows the
traffic amount of top 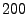 heavy hitters in two data sets. We can
see that the traffic distributions are highly skewed. heavy hitters in two data sets. We can
see that the traffic distributions are highly skewed.
Table 2:
Data Set Information
|
|
BELL-02 |
TERA-04 |
|
Time |
2002/05/19 (1-2PM) |
2004/02/09 (8-9AM) |
|
Volume |
8.371 GB |
0.106 GB |
|
Figure 1:
Traffic amount of top 200 hitters in BELL-02 and TERA-04
 |
We use a relative error metric to evaluate the estimation.
When evaluating an estimate for a specific key 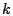 , we use , we use
This metric gets close to 0 when the estimation is accurate and it
can indicate whether we have overestimated or underestimated results.
When we evaluate the estimation result as a whole, we use the average
error
as a metric, where 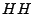 is the set of heavy hitters of our interest.
The square of point error metric is used to avoid cancellation between
positive and negative errors. is the set of heavy hitters of our interest.
The square of point error metric is used to avoid cancellation between
positive and negative errors.
4.3 Accuracy
Figure 2:
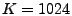 , , 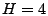 , , 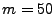 :
lsquare shows more accurate and stable estimation than countmin. :
lsquare shows more accurate and stable estimation than countmin.
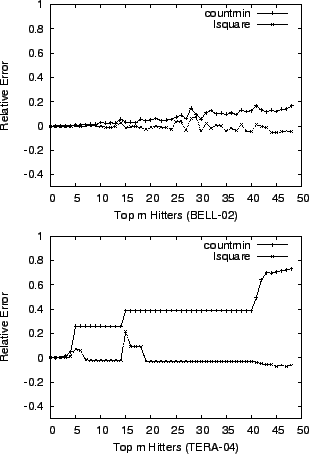 |
We first compare the accuracy of lsquare and countmin
when a single variable 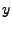 is used to capture the background noise
(caused by keys not in is used to capture the background noise
(caused by keys not in 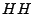 ). As a preliminary experiment, we calculate
the estimation errors for top 50 heavy hitters using the two methods,
with ). As a preliminary experiment, we calculate
the estimation errors for top 50 heavy hitters using the two methods,
with 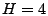 and and 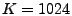 (Figure 2). We observe
that the accuracy of countmin fluctuates depending on the
data sets, whereas lsquare consistently gives more stable and
accurate estimates. (Figure 2). We observe
that the accuracy of countmin fluctuates depending on the
data sets, whereas lsquare consistently gives more stable and
accurate estimates.
Figure 3:
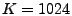 , , 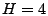 , , 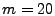 :
lsquare shows better accuracy when we use more noise variables. :
lsquare shows better accuracy when we use more noise variables.
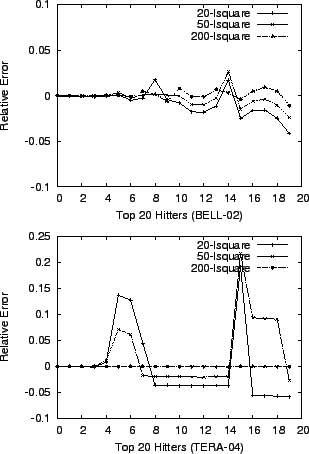 |
We next demonstrate that better accuracy can be achieved when we use
more variables to capture the noise effects. In
Figure 3 we evaluate the accuracy of lsquare
with a varying number of noise variables. For each data set, we
calculate the estimation errors of top 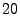 heavy hitters in three
cases. In the case of experiment `` heavy hitters in three
cases. In the case of experiment ``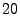 -lsquare'', just one
noise variable -lsquare'', just one
noise variable 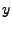 is used. Then top is used. Then top 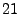 - -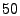 hitters are
considered as noise variables (in addition to hitters are
considered as noise variables (in addition to 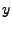 ) in experiment
`` ) in experiment
``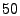 -lsquare'', and top -lsquare'', and top 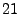 - -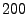 hitters in experiment
`` hitters in experiment
``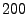 -lsquare.'' As more noise variables are used,
lsquare becomes more stable and accurate. In particular,
lsquare has almost no errors in the case of
`` -lsquare.'' As more noise variables are used,
lsquare becomes more stable and accurate. In particular,
lsquare has almost no errors in the case of
``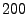 -lsquare.'' -lsquare.''
In addition, lsquare produces accurate estimates even for
``light'' hitters. In Figure 4, we calculate
the estimation errors for top 200 hitters. In BELL-02 data set,
lsquare shows relatively accurate estimation for top 160
hitters, where countmin is only good for top 40 hitters. We
observe bigger accuracy difference between the two methods in TERA-04
data set: lsquare still has accurate estimation for top 170
hitters but countmin has good performance only for top 20
hitters. Moreover, the accuracy of countmin for light hitters
is significantly lower.
Figure 4:
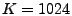 , , 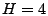 , , 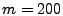 :
lsquare achieves good accuracy even for light hitters. :
lsquare achieves good accuracy even for light hitters.
 |
4.4 Tolerance with Limited Memory
Figure 5:
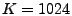 , ,
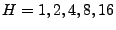 , ,
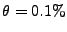 : The number of
hash tables has little impact on accuracy. lsquare
consistently shows better accuracy than countmin. : The number of
hash tables has little impact on accuracy. lsquare
consistently shows better accuracy than countmin.
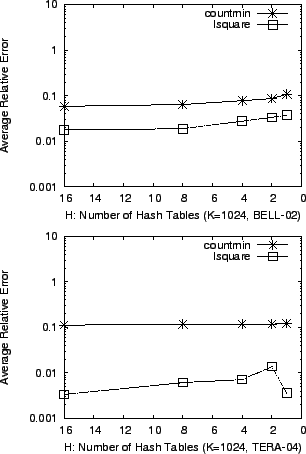 |
Figure 6:
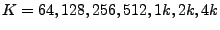 , , 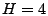 , ,
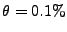 : The
number of buckets in a hash table has a big impact on accuracy. The
accuracy of lsquare degrades more gracefully as the number of
buckets decreases. : The
number of buckets in a hash table has a big impact on accuracy. The
accuracy of lsquare degrades more gracefully as the number of
buckets decreases.
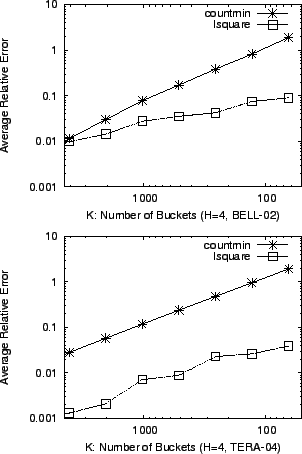 |
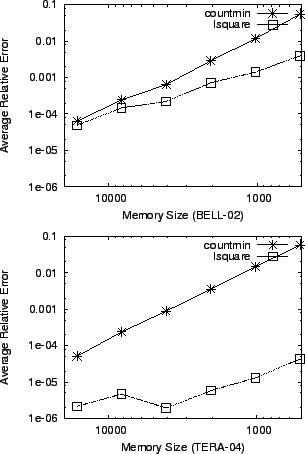
Figure 7:
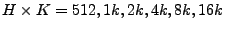 , ,
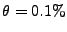 : For
each memory size, we find the optimal sketch configuration for
countmin. In that optimal configuration, we compare the
accuracy of lsquare and countmin. In both data sets,
lsquare shows better performance. : For
each memory size, we find the optimal sketch configuration for
countmin. In that optimal configuration, we compare the
accuracy of lsquare and countmin. In both data sets,
lsquare shows better performance.
 |
We now evaluate the accuracy of countmin and lsquare
under the constraint of limited memory. Since a sketch is usually
located within an expensive memory SRAM for high-speed traffic
monitoring, it is desirable to have accurate point estimates even if
we reduce the size of the sketch.
First, we fix the number of buckets in a hash table  to be to be 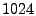 and vary the number of hash tables
and vary the number of hash tables 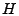 . Next, we vary . Next, we vary 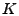 with fixed with fixed
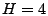 . In Figure 5 and 6, we
calculate the average error of the two methods for each sketch
configuration. We can see clearly that the accuracy of lsquare
degrades gracefully as the sketch gets smaller, whereas
countmin gives inaccurate estimates in memory-limited
situations. . In Figure 5 and 6, we
calculate the average error of the two methods for each sketch
configuration. We can see clearly that the accuracy of lsquare
degrades gracefully as the sketch gets smaller, whereas
countmin gives inaccurate estimates in memory-limited
situations.
To make the experiment more reliable regardless of the sketch
configuration, we find the optimal combination for countmin in
the given memory size after trying various combinations of 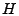 and and
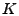 . Within the configuration where countmin shows the best
accuracy, we evaluate the accuracy of lsquare. Once again, we
observe better accuracy of the proposed method
(Figure 7). . Within the configuration where countmin shows the best
accuracy, we evaluate the accuracy of lsquare. Once again, we
observe better accuracy of the proposed method
(Figure 7).
We have implemented our lsquare method in Matlab. The most
time-consuming process in our method is solving the linear system
 . We make a preliminary evaluation regarding
the time performance of our implementation using a Pentium3-733MHz
machine with 128 MBytes memory, operated by Linux Debian 3.0. In this
experiment, we use a fixed sketch configuration (H=4, K=1024) and vary
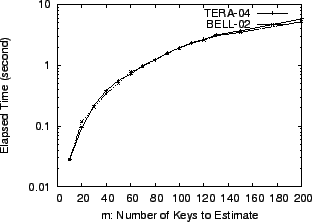
the number of heavy hitters we want to estimate. The results in
Figure 8 show that the linear program solver can compute point
estimations of 100 heavy hitters in about 2 seconds in the given
configuration. We note that our current Matlab implementation has not
been fully optimized and there is considerable room for further
speedup. For example, we can replace the pseudoinverse function pinv with an iterative least-squares solver such as lsqr to
take advantage of the sparsity of matrix . We make a preliminary evaluation regarding
the time performance of our implementation using a Pentium3-733MHz
machine with 128 MBytes memory, operated by Linux Debian 3.0. In this
experiment, we use a fixed sketch configuration (H=4, K=1024) and vary
the number of heavy hitters we want to estimate. The results in
Figure 8 show that the linear program solver can compute point
estimations of 100 heavy hitters in about 2 seconds in the given
configuration. We note that our current Matlab implementation has not
been fully optimized and there is considerable room for further
speedup. For example, we can replace the pseudoinverse function pinv with an iterative least-squares solver such as lsqr to
take advantage of the sparsity of matrix 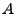 . .
Figure 8:
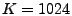 , , 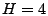 :
This graph shows the elapsed time to execute the Linear System Solver with various numbers of heavy hitters. :
This graph shows the elapsed time to execute the Linear System Solver with various numbers of heavy hitters.
 |
5 Conclusion and Future Work
In this paper, we propose a new approach for point estimation on
sketches. Using extensive experiments with real Internet data sets, we
show that the proposed method lsquare is much more accurate
than the best existing method countmin. lsquare
achieves good reconstruction accuracy for both heavy and light
hitters, at the expense of modest computation. Moreover, we have
shown that the accuracy of lsquare degrades gracefully as
memory decreases. To achieve accuracy comparable to countmin,
lsquare in general requires much less memory.
This paper represents an early example on how traditional statistical
inference techniques can be applied in the data stream context to
infer characteristics of the input stream. Existing research on data
stream computation so far has mainly focused on developing techniques
that provide provable worst-case accuracy guarantees. Statistical
inference techniques in contrast often pay more attention to
properties like likelihood, unbiasedness, estimation variance etc.
While these inference techniques may not provide any worst-case
accuracy guarantees, they often perform very well on practical
problems. In our future work, we plan to further explore how
statistical inference techniques can be applied to data stream
computation.
- 1
-
N. Alon, Y. Matias, and M. Szegedy.
The space complexity of approximating the frequency moments.
Journal of Computer and System Sciences, 58(1):137-147, 1999.
- 2
-
Bell Labs I data set, 2002.
https://pma.nlanr.net/Traces/long/bell1.html.
- 3
-
M. Charikar, K. Chen, and M. Farach-Colton.
Finding frequent items in data streams.
In Proceedings of ICALP '2002, pages 693-703, 2002.
https://www.cs.princeton.edu/~moses/papers/frequent.ps.
- 4
-
G. Cormode and S. Muthukrishnan.
What's hot and what's not: Tracking most frequent items dynamically.
In Proceedings of ACM PODC '2003, July 2003.
- 5
-
G. Cormode and S. Muthukrishnan.
An improved data stream summary: The count-min sketch and its
applications.
Proceedings of Latin American Theoretical Informatics (LATIN),
pages 29-38, 2004.
- 6
-
C. Estan and G. Varghese.
New directions in traffic measurement and accounting.
Proceedings of ACM SIGCOMM, 2002.
- 7
-
P. Gibbons and Y. Matias.
Synopsis structures for massive data sets.
DIMACS Series in Discrete Mathematics and Theoretical Computer
Science, 1999.
- 8
-
B. Krishnamurthy, S. Sen, Y. Zhang, and Y. Chen.
Sketch-based change detection: Methods, evaluation, and applications.
Proceedings of ACM SIGCOMM Internet Measurement Conference,
2003.
- 9
-
A. Kumar, M. Sung, J. Xu, and J. Wang.
Data streaming algorithms for efficient and accurate estimation of
flow distribution.
Proceedings of ACM Sigmetrics/Performance, 2004.
- 10
-
E. H. Moore.
On the reciprocal of the general algebraic matrix.
Bulletin of the American Mathematical Society, 26:394-395,
1920.
- 11
-
S. Muthukrishnan.
Data streams: Algorithms and applications, 2003.
Manuscript based on invited talk from 14th SODA. Available from
https://www.cs.rutgers.edu/~muthu/stream-1-1.ps.
- 12
-
NLANR.
https://www.nlanr.net/.
- 13
-
R. Penrose.
A generalized inverse of matrices.
Mathematical Proceedings of the Cambridge Philosophical
Society, 51:406-412, 1955.
- 14
-
R. Schweller, A. Gupta, Y. Chen, and E. Parsons.
Reversible sketches for efficient and accurate change detection over
network data streams.
Proceedings of ACM SIGCOMM Internet Measurement Conference,
pages 207-212, 2004.
- 15
-
Teragrid-I 10GigE trace, 2004.
https://pma.nlanr.net/Special/tera1.html.
Improving Sketch Reconstruction Accuracy
Using Linear Least Squares Method
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -image_type gif paper.tex
The translation was initiated by Yin Zhang on 2005-08-09


Yin Zhang
2005-08-09
|
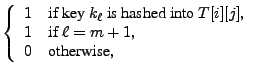
![]() is not a square matrix and may be rank deficient. In
this case, a standard solution to
is not a square matrix and may be rank deficient. In
this case, a standard solution to
![]() is the
pseudoinverse solution
is the
pseudoinverse solution
![]() , where
, where ![]() is
the pseudoinverse (i.e., Moore-Penrose inverse [10,13]) of matrix
is
the pseudoinverse (i.e., Moore-Penrose inverse [10,13]) of matrix ![]() . It is known that
. It is known that
![]() provides the shortest length least squares solution to the
system of linear equations
provides the shortest length least squares solution to the
system of linear equations
![]() . More precisely,
it solves:
. More precisely,
it solves:
![]() and the countmin estimation as an upper
bound. The pseudo-code for the resulting algorithm is given as follows.
and the countmin estimation as an upper
bound. The pseudo-code for the resulting algorithm is given as follows.
![]() to capture the effects
of background noise. This assumes that we do not know any keys other
than those of our direct interest. In case we do know extra keys, we
can add them to
to capture the effects
of background noise. This assumes that we do not know any keys other
than those of our direct interest. In case we do know extra keys, we
can add them to ![]() and treat the corresponding
and treat the corresponding ![]() as
additional noise variables. We will show in
Section 4.3 that the use of additional noise
variables significantly improves the accuracy of lsquare.
as
additional noise variables. We will show in
Section 4.3 that the use of additional noise
variables significantly improves the accuracy of lsquare.
![]() heavy hitters in two data sets. We can
see that the traffic distributions are highly skewed.
heavy hitters in two data sets. We can
see that the traffic distributions are highly skewed.
![]() , we use
, we use
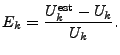
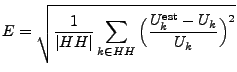
![]() is used to capture the background noise
(caused by keys not in
is used to capture the background noise
(caused by keys not in ![]() ). As a preliminary experiment, we calculate
the estimation errors for top 50 heavy hitters using the two methods,
with
). As a preliminary experiment, we calculate
the estimation errors for top 50 heavy hitters using the two methods,
with ![]() and
and ![]() (Figure 2). We observe
that the accuracy of countmin fluctuates depending on the
data sets, whereas lsquare consistently gives more stable and
accurate estimates.
(Figure 2). We observe
that the accuracy of countmin fluctuates depending on the
data sets, whereas lsquare consistently gives more stable and
accurate estimates.
![]() heavy hitters in three
cases. In the case of experiment ``
heavy hitters in three
cases. In the case of experiment ``![]() -lsquare'', just one
noise variable
-lsquare'', just one
noise variable ![]() is used. Then top
is used. Then top ![]() -
-![]() hitters are
considered as noise variables (in addition to
hitters are
considered as noise variables (in addition to ![]() ) in experiment
``
) in experiment
``![]() -lsquare'', and top
-lsquare'', and top ![]() -
-![]() hitters in experiment
``
hitters in experiment
``![]() -lsquare.'' As more noise variables are used,
lsquare becomes more stable and accurate. In particular,
lsquare has almost no errors in the case of
``
-lsquare.'' As more noise variables are used,
lsquare becomes more stable and accurate. In particular,
lsquare has almost no errors in the case of
``![]() -lsquare.''
-lsquare.''



![]() to be
to be ![]() and vary the number of hash tables
and vary the number of hash tables ![]() . Next, we vary
. Next, we vary ![]() with fixed
with fixed
![]() . In Figure 5 and 6, we
calculate the average error of the two methods for each sketch
configuration. We can see clearly that the accuracy of lsquare
degrades gracefully as the sketch gets smaller, whereas
countmin gives inaccurate estimates in memory-limited
situations.
. In Figure 5 and 6, we
calculate the average error of the two methods for each sketch
configuration. We can see clearly that the accuracy of lsquare
degrades gracefully as the sketch gets smaller, whereas
countmin gives inaccurate estimates in memory-limited
situations.
![]() and
and
![]() . Within the configuration where countmin shows the best
accuracy, we evaluate the accuracy of lsquare. Once again, we
observe better accuracy of the proposed method
(Figure 7).
. Within the configuration where countmin shows the best
accuracy, we evaluate the accuracy of lsquare. Once again, we
observe better accuracy of the proposed method
(Figure 7).
![]() . We make a preliminary evaluation regarding
the time performance of our implementation using a Pentium3-733MHz
machine with 128 MBytes memory, operated by Linux Debian 3.0. In this
experiment, we use a fixed sketch configuration (H=4, K=1024) and vary
the number of heavy hitters we want to estimate. The results in
Figure 8 show that the linear program solver can compute point
estimations of 100 heavy hitters in about 2 seconds in the given
configuration. We note that our current Matlab implementation has not
been fully optimized and there is considerable room for further
speedup. For example, we can replace the pseudoinverse function pinv with an iterative least-squares solver such as lsqr to
take advantage of the sparsity of matrix
. We make a preliminary evaluation regarding
the time performance of our implementation using a Pentium3-733MHz
machine with 128 MBytes memory, operated by Linux Debian 3.0. In this
experiment, we use a fixed sketch configuration (H=4, K=1024) and vary
the number of heavy hitters we want to estimate. The results in
Figure 8 show that the linear program solver can compute point
estimations of 100 heavy hitters in about 2 seconds in the given
configuration. We note that our current Matlab implementation has not
been fully optimized and there is considerable room for further
speedup. For example, we can replace the pseudoinverse function pinv with an iterative least-squares solver such as lsqr to
take advantage of the sparsity of matrix ![]() .
.



![$\displaystyle \begin{tabular}{\vert c\vert c\vert c\vert c\vert}
\cline{2-4}
\m...
...line
$T[1][j]$ & $14^{0,3}$ & $19^{2,4}$ & $4^{1}$ \\
\hline
\end{tabular}$](img55.gif)
![$\displaystyle {%\scriptsize
\mathbf{x} =
\left[ \begin{array}{c}
x_{3} \ x_{4}...
...\ 0 & 0 & 1 \ 1 & 0 & 1 \ 0 & 1 & 1 \ 0 & 0 & 1 \\
\end{array} \right].
}
$](img72.gif)



