



Next: AMP Algorithm
Up: AMP
Previous: Replacement Policy for Prefetched
Theoretical Analysis: Optimality Criteria
In this section we theoretically analyze the case when an LRU cache is
shared by prefetched data for multiple steady sequential streams.
We assume an AA algorithm operating with a cache of size 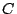 .
. 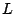 is
defined as the average life of a page in the cache.
Each stream has a maximum request rate,
is
defined as the average life of a page in the cache.
Each stream has a maximum request rate, 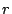 , which is achieved
when all read requests are hits in the cache.
The aggregate throughput,
, which is achieved
when all read requests are hits in the cache.
The aggregate throughput, 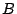 , is the sum of individual stream throughputs
(
, is the sum of individual stream throughputs
(
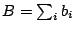 ).
).
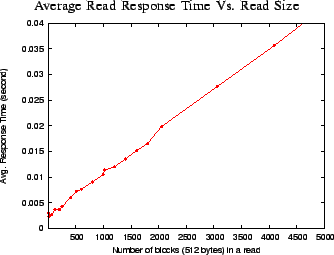
Figure 2:
Starting at 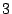 ms, the average response time grows linearly with the read size.
We observed similar behavior for RAID-
ms, the average response time grows linearly with the read size.
We observed similar behavior for RAID-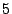 implying that the
optimality criteria in this paper apply to RAID as well.
implying that the
optimality criteria in this paper apply to RAID as well.
 |
Observation 3.1
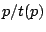 is a monotonically non-decreasing function, where
is a monotonically non-decreasing function, where 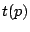 is the
average time to prefetch
is the
average time to prefetch  pages.
pages.
Proof.
From Figure
2 we observe that
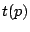
is of the form
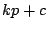
.
Hence,
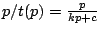
, and its slope
is positive since
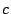
is positive.

Definition 3.1
A stream is said to be satisfied at 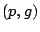 , if it experiences no
misses for the given
, if it experiences no
misses for the given  and
and  .
.
Proof.
By definition, if a stream is satisfied at
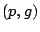
then it experiences no
misses in the steady state. That implies that the prefetch issued at the trigger
distance

completes before the
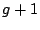
pages are read by the client.
Therefore,
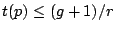
, where
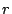
is the request rate of the stream.
The reverse is also true. If the
time it takes to prefetch

pages is not more than the time it takes the
client to read the

pages, then there cannot be any misses in the steady state
implying that the stream is satisfied.

Observation 3.2
The throughput of a satisfied stream is equal to 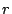 , its request rate.
, its request rate.
Proof.
By definition, a satisfied stream experiences no misses in the steady state.
No misses implies no stall time and the stream proceeds at its
desired request rate of
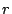
.

Proof.
If
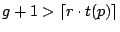
then
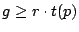
or
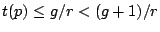
.
By Lemma
III.1, the stream is satisfied at the chosen
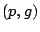
but is also satisfied for
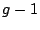
at
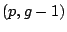
.
By Observation
III.2, the throughput with
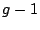
will remain the
same as the stream will remain satisfied.
However, the cost of the case where a lower

is used is
smaller as the average number of pages that have to be kept in the
cache is smaller. Hence, cache space is being wasted without any gain in
throughput.

Lemma 3.3
If there is no cache pollution, wastage occurs iff 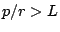 .
.
Proof.
If there is no cache pollution,
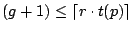
(Lemma
III.2).
By their definitions,

pages are requested when
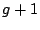
pages from the
previous prefetch are still unaccessed. The number
of these pages that are consumed in the time it takes to prefetch is
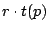
,
which is roughly all of the unaccessed pages.
Hence, as soon as the next

pages are prefetched, they begin to be consumed
at the request rate
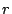
. Therefore, the time it takes for the

pages
to be consumed after prefetch is
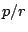
. Now, if the
average life (
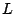
) of pages in the cache is less than
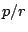
, then some of the
prefetched pages will be evicted before they are requested. Conversely, if
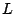
is greater than
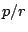
then all the

pages will be requested before
they reach the LRU end of the list and face eviction.

Lemma 3.4
If there is no cache pollution, throughput of a stream (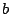 ) =
) =
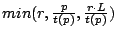 .
.
Proof.
The throughput of a stream cannot exceed its request rate (
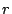
).
Further, since we use a single outstanding prefetch for a stream at any time,
the throughput cannot exceed the amount prefetched (

) divided by the
time it takes to prefetch that amount
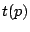
. In the case where
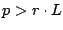
,
wastage occurs (Lemma
III.3) and only
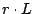
pages out of

will be accessed before being evicted. In this case, the
throughput is limited by
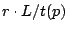
.

Proof.
The life of the cache (
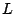
) is equal to the time it takes to insert
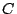
new pages in
the top end of the cache. If there is no wastage, the rate of insertion in the
cache is equal to the aggregate read throughput of all the streams (
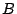
).
Therefore,
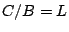
.

Lemma 3.6
For a fixed choice of
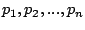 , and cache of size
, and cache of size 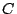 , the aggregate throughput (
, the aggregate throughput (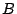 ) is unique when there is no wastage.
) is unique when there is no wastage.
Proof.
Suppose, the aggregate throughput(
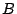
) was not unique.
Without loss of generality, we would have
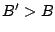
, such that
Since there is no wastage, we have
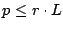 for all streams.
So, the only different term in the
for all streams.
So, the only different term in the 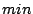 expression is not significant.
Thus,
expression is not significant.
Thus, 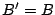 , which is contrary to our assumption.
, which is contrary to our assumption.

Theorem 3.1
The aggregate throughput of 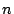 streams sharing a cache of size
streams sharing a cache of size 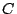 with average cache life
with average cache life 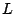 ,
is maximized if
,
is maximized if
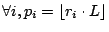 .
.
Proof.
Given
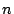
streams with request rates of
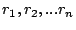
and a cache of size
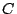
, let the throughput obtained by the choice:
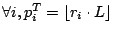
be
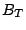
. The theorem claims that
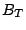
is the maximum aggregate bandwidth obtainable (
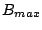
)
through any choice of
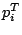
.
We will prove by contradiction. Let us assume that
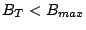 .
Therefore, there exists some choice of
.
Therefore, there exists some choice of
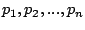 such that the
aggregate bandwidth of all streams is
such that the
aggregate bandwidth of all streams is 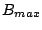 .
.
Since wastage and cache pollution can never increase aggregate throughput,
we assume, without loss of generality, that 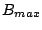 is free from these inefficiencies.
is free from these inefficiencies.
If the choice of 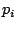 is the same as that specified by this theorem, then by
Lemma III.6,
is the same as that specified by this theorem, then by
Lemma III.6,
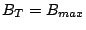 , which is contrary
to our assumption.
, which is contrary
to our assumption.
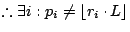 |
(1) |
By Lemma III.3, it must be the case for 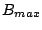 that
that
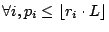 |
(2) |
If follows from (1) and (2), without loss of generality,
that
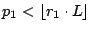 .
.
Let us define a new set:
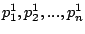 ,
where
,
where
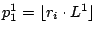 , and
, and
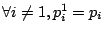 .
.
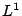 and
and 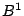 are the new cache life and aggregate throughput values.
are the new cache life and aggregate throughput values.
Since
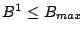 (by defn. of
(by defn. of 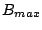 ),
),
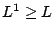 (Lemma III.5). By Lemma III.4,
(Lemma III.5). By Lemma III.4,
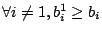 as
as
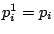 and
and
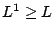 . By
Observation III.1 and Lemma III.4,
. By
Observation III.1 and Lemma III.4,
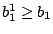 as
as
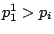 .
.
Since
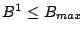
, it follows that
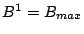
.
By repeating the above procedure for every stream with
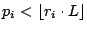 , we will arrive at a set
, we will arrive at a set
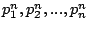 , where
, where
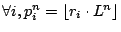 and
and
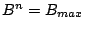 .
.
Since, the choice of  for each stream will then be the same for
for each stream will then be the same for
 and
and 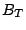 ,
, 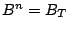 by Lemma III.6.
by Lemma III.6.
which contradicts our assumption that
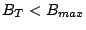
.




Next: AMP Algorithm
Up: AMP
Previous: Replacement Policy for Prefetched
root
2006-12-19



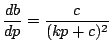
![]() for all streams.
So, the only different term in the
for all streams.
So, the only different term in the ![]() expression is not significant.
Thus,
expression is not significant.
Thus, ![]() , which is contrary to our assumption.
, which is contrary to our assumption.
![]()
![]() .
Therefore, there exists some choice of
.
Therefore, there exists some choice of
![]() such that the
aggregate bandwidth of all streams is
such that the
aggregate bandwidth of all streams is ![]() .
.
![]() is free from these inefficiencies.
is free from these inefficiencies.
![]() is the same as that specified by this theorem, then by
Lemma III.6,
is the same as that specified by this theorem, then by
Lemma III.6,
![]() , which is contrary
to our assumption.
, which is contrary
to our assumption. ![]() that
that
![]() .
.
![]() ,
where
,
where
![]() , and
, and
![]() .
.
![]() and
and ![]() are the new cache life and aggregate throughput values.
are the new cache life and aggregate throughput values.
![]() (by defn. of
(by defn. of ![]() ),
),
![]() (Lemma III.5). By Lemma III.4,
(Lemma III.5). By Lemma III.4,
![]() as
as
![]() and
and
![]() . By
Observation III.1 and Lemma III.4,
. By
Observation III.1 and Lemma III.4,
![]() as
as
![]() .
.
![]() , we will arrive at a set
, we will arrive at a set
![]() , where
, where
![]() and
and
![]() .
.
![]() for each stream will then be the same for
for each stream will then be the same for
![]() and
and ![]() ,
, ![]() by Lemma III.6.
by Lemma III.6.