Non-Transitive Connectivity and DHTs

Michael J. Freedman, Karthik Lakshminarayanan, Sean Rhea, and Ion Stoica

New York University and University of California, Berkeley
mfreed@cs.nyu.edu, {karthik,srhea,istoica}@cs.berkeley.edu

1 Introduction

The most basic functionality of a distributed hash table, or DHT, is to partition a key space across the set of nodes in a distributed system such that all nodes agree on the partitioning. For example, the Chord DHT assigns each node a random identifier from the key space of integers modulo 2¹⁶⁰ and maps each key to the node whose identifier most immediately follows it. Chord is thus said to implement the successor relation, and so long as each node in the network knows its predecessor in the key space, any node can compute which keys are mapped onto it.

An implicit assumption in Chord and other DHT protocols is that all nodes are able to communicate with each other, yet we know this assumption is unfounded in practice. We say a set of three hosts, A, B, and C, exhibit non-transitivity if A can communicate with B, and B can communicate with C, but A cannot communicate with C. As we show in Section 2, 2.3% of all pairs of nodes on PlanetLab exhibit transient periods in which they cannot communicate with each other, but in which they can communicate through a third node. These transient periods of non-transitivity occur for many reasons, including link failures, BGP routing updates, and ISP peering disputes (e.g., [13]).

Such non-transitivity in the underlying network is problematic for DHTs. Consider for example the Chord network illustrated in Figure 1. Identifiers increase from the left, so node B is the proper successor to key k. If nodes A and B are unable to communicate with each other, A will believe that C is its successor. Upon receiving a lookup request for k, A will return C to the requester. If the requester then tries to insert a document associated with k at node C, node C would refuse, since according to its view it is not responsible for key k.

While this example may seem contrived, it is in fact quite common. If each pair of nodes with adjacent identifiers in a 300-node Chord network (independently) has a 0.1% chance of being unable to communicate, then we expect that there is a 1-0.999³⁰⁰ » 26% chance that some pair will be unable to communicate at any time. However, both nodes in such a pair have a 0.999² chance of being able to communicate with the node that most immediately precedes them both.

Collectively, the authors have produced three independent DHT implementations: the Bamboo [18] implementation in OpenDHT [19], the Chord [23] implementation in i3 [22], and the Kademlia [11] implementation in Coral [8]. Moreover, we have run public deployments of these three DHTs on PlanetLab for over a year.

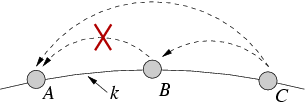Figure 1: Non-transitivity in Chord. The dashed lines represent predecessor links.

While DHT algorithms seem quite elegant on paper, in practice we found that a great deal of our implementation effort was spent discovering and fixing problems caused by non-transitivity. Of course, maintaining a full link-state routing table at each DHT node would have sufficed to solve all such problems, but would also require considerably more bandwidth than a basic DHT.¹ Instead, we each independently discovered a set of "hacks" to cover up the false assumption of full connectivity on which DHTs are based.

In this paper, we categorize the ways in which Bamboo, Chord, and Kademlia break down under non-transitivity, and we enumerate the ways we modified them to cope with these shortcomings. We also discuss application-level solutions to the problem. Many of these failure modes and fixes were quite painful for us to discover, and we hope that-at least in the short term-this work will save others the effort. In the longer term, we hope that by focusing attention on the problem, we will encourage future DHT designers to tackle non-transitivity head-on.

The next section quantifies the prevalence of non-transitivity on the Internet and surveys related work in this area. Section 3 presents a brief review of DHT terminology. Section 4 discusses four problems caused by non-transitivity in DHTs and our solutions to them. Finally, Section 5 concludes.

2 Prevalence of Non-Transitivity

The Internet is known to suffer from network outages (such as extremely heavy congestion or routing convergence problems) that result in the loss of connectivity between some pairs of nodes [14,3]. Furthermore, the loss of connectivity is often non-transitive; in fact, RON [3] and SOSR [10] take advantage of such non-transitivity-the fact that two nodes that cannot temporarily communicate with one another often have a third node that can communicate with them both-to improve resilience by routing around network outages.

Gerding and Stribling [9] observed a significant degree of non-transitivity among PlanetLab hosts; of all possible unordered three tuples of nodes (A,B,C), about 9% exhibited non-transitivity. Furthermore, they attributed this non-transitivity to the fact that PlanetLab consists of three classes of nodes: Internet1-only, Internet2-only, and multi-homed nodes. Although Internet1-only and Internet2-only nodes cannot directly communicate, multi-homed nodes can communicate with them both.

Extending the above study, we have found that transient routing problems are also a major source of non-transitivity in PlanetLab. In particular, we considered a three hour window on August 3, 2005 from the all-pairs ping dataset [1]. The dataset consists of pings between all pairs of nodes conducted every 15 minutes, with each data point averaged over ten ping attempts.

We counted the number of unordered pairs of hosts (A,B) such that A and B cannot reach each other but another host C can reach both A and B. We found that, of all pairs of nodes, about 5.2% of them belonged to this category over the three hour window. Of these pairs of nodes, about 56% of the pairs had persistent problems; these were probably because of the problem described above. However, the remaining 44% of the pairs exhibited problems intermittently; in fact, about 25% of the pairs could not communicate with each other only in one of the 15-minute snapshots. This suggests that non-transitivity is not entirely an artifact of the PlanetLab testbed, but also caused by transient routing problems.

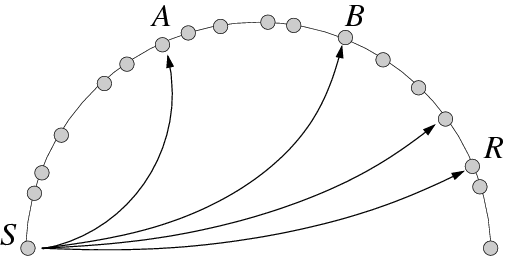Figure 2: Two styles of DHT routing for source node S to perform a lookup that terminates at root node R.

3 DHT Background

Before moving on to the core of this paper, we first briefly review basic DHT nomenclature. We assume the reader has some familiarity with basic DHT routing protocols. For more information, see [23,11,21].

The DHT assigns every key in the identifier space to a node, which is called the root (or the successor) of the key. The main primitive that DHTs support is lookup, in which a node can efficiently discover a key's root. The lookup protocol greedily traverses the nodes of the DHT, progressing closer to the root of the key at each step.

Each node maintains a set of neighbors that it uses to route packets. Typically, such neighbors are divided into (a) short links chosen from the node's immediate neighborhood in the ID space to ensure correctness of lookups, and (b) long links chosen to ensure that lookups are efficient (e.g., take no more than O(logn) hops for a network with n nodes). In Chord and Bamboo, the set of short links is called the node's successor list and leaf set, respectively, and the long links are called fingers and routing table entries. While Kademlia uses a single routing table, one can still differentiate between its closest bucket of short links and farther buckets of long links.

DHT routing can be either iterative or recursive [7] (see Figure 2). Consider a simple example, in which source node S initiates a lookup for some key whose root is node R. In iterative routing, node S first contacts node A to learn about node B, and then S subsequently contacts B. In recursive routing, S contacts A, and A contacts B in turn.

Both routing techniques have different strengths. For example, recursive routing is faster than iterative routing using the same bandwidth budget [7,17] and can use faster per-node timeouts [18]. On the other hand, iterative routing gives the initiating node more end-to-end control, which can be used, for instance, for better parallelization [11,17]. We discuss the impact of both approaches in the following section.

4 Problems and Solutions

This section presents problems caused by non-transitivity in DHTs and the methods we use to mitigate them. We present these problems in increasing order of how difficult they are to solve.

4.1 Invisible Nodes

One problem due to non-transitivity occurs when a node learns about system participants from other nodes, yet cannot directly communicate with these newly discovered nodes. This problem arises both during neighbor maintenance and while performing lookups.

For example, assume that a node A learns about a potential neighbor B through a third node C, but A and B cannot directly communicate. We say that from A's perspective B is an invisible node. In early versions of both Bamboo and i3-Chord, A would blindly add B as a neighbor. Later, A would notice that B was unreachable and remove it, but in the meantime A would try to route messages through B.

A related problem occurs when nodes blindly trust failure notifications from other nodes. Continuing the above example, when A fails to contact B due to non-transitivity, in a naive implementation A will inform C of this fact, and C will erroneously remove B as a neighbor.

A simple fix for both of these problems is to prevent nodes from blindly trusting other nodes with respect to which nodes in the network are up or down. Instead, a node A should only add a neighbor B after successfully communicating with it, and A should only remove a neighbor with whom it can no longer directly communicate. This technique is used by all three of our DHTs.

Figure 3: Invisible nodes. S learns about M and N from A while trying to route to R, but S has no direct connectivity to M. By sending lookup messages to M and N in parallel, S avoids being stalled while its request to M times out.

Invisible nodes also cause performance problems during iterative routing, where the node performing a lookup must communicate with nodes that are not its immediate neighbors in the overlay. For example, as shown in Figure 3, a node S may learn of another node M through its neighbor A, but may be unable to directly communicate with M to perform a lookup. S will eventually time out its request to M, but such timeouts increase the latency of lookups substantially.

Three techniques can mitigate the effect of invisible nodes on lookup performance in iterative routing. First, a DHT can use virtual coordinates such as those computed by Vivaldi [6] to choose tighter timeouts. This technique should work well in general, although we have found that the Vivaldi implementations in both Bamboo and Coral are too inaccurate on PlanetLab to be of much use.²

Second, a node can send several messages in parallel for each lookup, allowing requests to continue towards the root even when some others time out. As shown in Figure 3, S can send lookup messages to M and N in parallel. This technique was first proposed in Kademlia [11].

Third, a node can remember other nodes that it was unable to reach in the past. Using this technique, which we call a unreachable node cache, a node S marks M as unreachable after a few failed communication attempts. Then, if M is encountered again during a subsequent lookup request, S immediately concludes that it is unreachable without wasting bandwidth and suffering a timeout.

OpenDHT and i3 both use recursive routing, but Coral implements iterative routing using the above approach, maintaining three parallel RPCs and a unreachable node cache.

4.2 Routing Loops

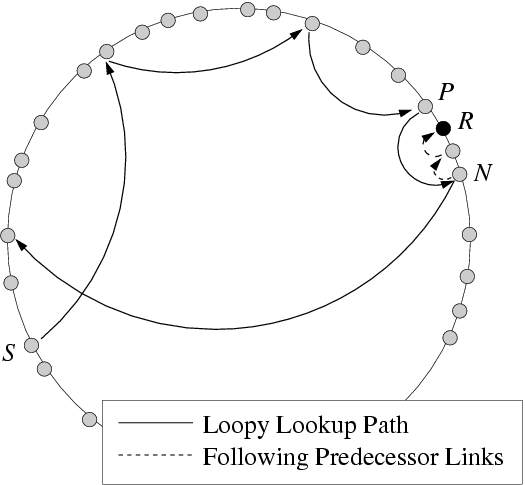Figure 4: Routing loops. In Chord, if a lookup passes by the correct successor on account of non-transitivity, a routing loop arises. The correctness of lookup can be improved in such cases by traversing predecessor links.

In Chord, non-transitivity causes routing loops as follows. The root for a key k in Chord is the node whose identifier most immediately succeeds k in the circular key space. In Figure 4, let the proper root for k be R. Also, assume that P cannot communicate with R. A lookup routed through P thus skips over R to N, the next node in the key space with which P can communicate. N, however, knows its correct predecessor in the network, and therefore knows that it is not the root for k. It thus forwards the lookup around the ring, and a loop is formed.

Bamboo and Kademlia avoid routing loops by defining a total ordering over nodes during routing. In these networks, a node A only forwards a lookup on key k to another node B if |B-k| < |A-k|, where "-" represents modular subtraction in Bamboo and XOR in Kademlia.

Introducing such a total ordering in Chord is straightforward: instead of blindly forwarding a lookup towards the root, a node can stop any lookup that has already passed its root. For example, when N receives a lookup for k from P, it knows something is amiss since P < k < N, but N is not the direct successor of k.

Stopping a lookup in this way avoids loops, but it is often possible to get closer to the root for a key by routing along predecessor links once normal routing has stopped. i3's Chord implementation backtracks in this way. For example, the dashed lines from N back to R in Figure 4 show the path of the lookup using predecessor links. To guarantee termination when backtracking, once a packet begins following predecessor links it is never again routed along forward links.

4.3 Broken Return Paths

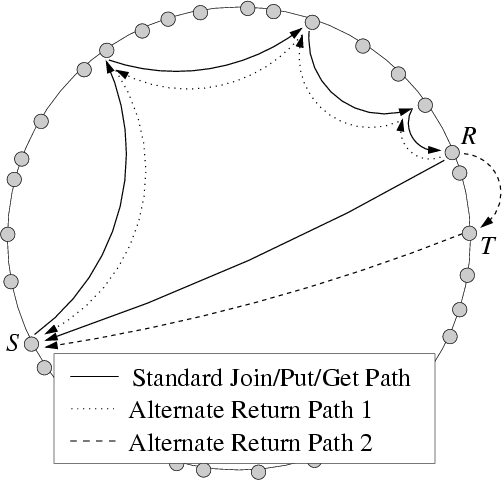Figure 5: Broken return paths. Although S can route a put or get request to R through the overlay, there may be no direct IP route back from R to S. One alternative is to route the result back along the path taken from S to R; the other is to route through a random neighbor T.

Often an application built atop a DHT routing layer wants to not only route to the root of a key but also to retrieve some value back. For example, it may route a put request to the root, in which case it expects an acknowledgment of its request in return. Likewise, with a get request, it expects to receive any values stored under the given key. In one very important case, it routes a request to join the DHT to the root and expects to receive the root's leaf set or successor list in return.

As shown in Figure 5, when a source S routes a request recursively to the root R, the most obvious and least costly way for R to respond is to communicate with S directly over IP. While this approach works well in the common case, it fails with non-transitivity; the existence of a route from S to R through the overlay does not guarantee the existence of the direct IP route back. We know of two solutions to this problem.

The first solution is to source route the message backwards along the path it traveled from S to R in the first place, as shown by the dotted line in Figure 5. Since each node along the path forwarded the message through a neighbor that had been responding to its probes for liveness, it is likely that this return path is indeed routable. A downside of this solution is that the message takes several hops to return to the client, wasting the bandwidth of multiple nodes.³

A less costly solution is to have R source route its response to S through a random member of its leaf set or successor list, as shown by the dashed line in Figure 5. These nodes are chosen randomly with respect to R itself (by the random assignment of node identifiers), so most of them are likely to be able to route to S. Moreover, we already know that R can route to them, or it would not have them as neighbors.

A problem with both of these solutions is that they waste bandwidth in the common case where R can indeed send its response directly to S. To avoid this waste, we have S acknowledge the direct response from R. If R fails to receive an acknowledgment after some timeout, R source routes the response back (either along the request path or through a single neighbor). This timeout can be chosen using virtual coordinates, although we have had difficulty with Vivaldi on PlanetLab as discussed earlier. Alternatively, we can simply choose a conservative timeout value: as it is used only in the uncommon case where R cannot route directly to S, it affects the latency of only a few requests in practice. Bamboo/OpenDHT routes back through a random leaf-set neighbor in the case of non-transitivity, using a timeout of five seconds.

We note that iterative routing does not directly suffer from this problem. Since S directs the routing process itself, it will assume R is down and look for an alternate root R' (i.e., the node that would be the root if R were actually down). Of course, depending on the application, R' may not be a suitable replacement for R, but that reduces to the inconsistent root problem, which we discuss next.

4.4 Inconsistent Roots

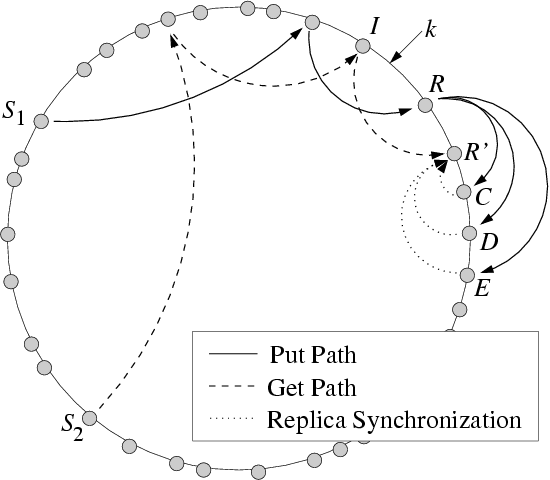Figure 6: Inconsistent roots. A put from S₁ is routed to the root, R, which should replicate it on R',C,D. But since R cannot communicate with R', it replicates it on C-E instead. R' will later acquire a replica during synchronization with C-E.

The problems we have discussed so far are all routing problems. In this section, we discuss a problem caused by non-transitivity that affects the correctness of the partitioning of the DHT key space.

Most DHT applications assume that there is only one root for a given key in the DHT at any given time. As shown in Figure 6, however, this assumption may be invalid in the presence of non-transitivity. In the figure, node R is the proper root of key k, but since R and R' cannot communicate, R' mistakenly believes it is the root for k. A lookup from S₁ finds the correct root, but a lookup from S₂ travels through node I, which also cannot communicate with R, and terminates instead at R'.

Prior work has explored the issue of multiple roots due to transient conditions created by nodes joining and leaving the overlay, but has not explored the effects of misbehavior in the underlying network [4].

Given a complete partition of the network, it is difficult to solve this problem at all, and we are not aware of any existing solutions to it. On the other hand, if the degree of non-transitivity is limited, the problem can be eliminated by the use of a consensus algorithm. The use of such algorithms in DHTs is an active area of research [12,20].

Nonetheless, consensus is expensive in messages and bandwidth, so many existing DHTs use a probabilistic approach to solving the problem instead. For example, FreePastry 1.4.1 maintains full link-state routing information for each leaf set, and a node is considered alive if any other member of its leaf set can route to it [2]. Once routability has been provided in this manner, existing techniques (e.g., [4]) can be used to provide consistency.

An alternative approach used by both DHash [5] and OpenDHT [16] is to solve the inconsistent root problem at the application layer. Consider the traditional put/get interface to hash tables. As shown in Figure 6, DHash sends a put request from S₁ for a key-value pair (k,v) to the r closest successors of k, each of which stores a replica of (k,v).⁴ In the figure, R cannot communicate with R', and hence the wrong set of nodes store replicas.

To handle this case, as well as normal failures, the nodes in each successor list periodically synchronize with each other to discover values they should be storing (see [5,16] for details). As shown in the figure, R' synchronizes with C-E and learns about the value put by S₁. A subsequent get request from S₂ which is routed to R' will thus find the value despite the non-transitivity.

Of course, if R' fails to synchronize with C-E between the put from S₁ and the get from S₂, it will mistakenly send an empty response for the get. To avoid this case, for each get request on key k, DHash and OpenDHT query multiple successors of k. For example, in the figure, R' would send the get request to C-E, and all four nodes would respond to S₂, which would then compile a combined response. This extra step increases correctness at the cost of increased latency and load; OpenDHT uses heuristics to decide when this extra step can be eliminated safely [17].

5 Conclusion

In this paper, we enumerated several ways in which naive DHT implementations break down under non-transitivity, and we presented our experiences in dealing with the problems when building and deploying three independent DHT-based systems-OpenDHT [19] that uses Bamboo [18], i3 [22] that uses Chord [23], and Coral [8] that uses Kademlia [11]. While we believe that the ultimate long-term answer to dealing with issues arising from non-transitivity is perhaps a fresh DHT design, we hope that, at least in the short term, this work will save others the effort of finding and fixing the problems we encountered.

References

[1]: PlanetLab All-Pairs Pings. http://pdos.lcs.mit.edu/~strib/pl_app/.
[2]: Freepastry release notes. http://freepastry.rice.edu/FreePastry/README-1.4.1.html, May 2005.
[3]: D. Andersen, H. Balakrishnan, F. Kaashoek, and R. Morris. Resilient Overlay Networks. In Proc. SOSP, 2001.
[4]: M. Castro, M. Costa, and A. Rowstron. Performance and dependability of structured peer-to-peer overlays. Technical Report MSR-TR-2003-94, Dec. 2003.
[5]: J. Cates. Robust and efficient data management for a distributed hash table. Master's thesis, Massachusetts Institute of Technology, May 2003.
[6]: F. Dabek, R. Cox, F. Kaahoek, and R. Morris. Vivaldi: A decentralized network coordinate system. In Proc. SIGCOMM, 2004.
[7]: F. Dabek, J. Li, E. Sit, J. Robertson, M. F. Kaashoek, and R. Morris. Designing a DHT for low latency and high throughput. In Proc. NSDI, 2004.
[8]: M. J. Freedman, E. Freudenthal, and D. Mazières. Democratizing content publication with Coral. In Proc. NSDI, Mar. 2004.
[9]: S. Gerding and J. Stribling. Examining the tradeoffs of structured overlays in a dynamic non-transitive network, 2003. Class project: http://pdos.csail.mit.edu/~strib/docs/projects/networking_fall2003.pdf.
[10]: K. P. Gummadi, H. V. Madhyastha, S. D. Gribble, H. M. Levy, and D. Wetherall. Improving the reliability of internet paths with one-hop source routing. In Proc. OSDI, 2002.
[11]: P. Maymounkov and D. Mazieres. Kademlia: A peer-to-peer information system based on the XOR metric. In Proc. IPTPS, 2002.
[12]: A. Muthitacharoen, S. Gilbert, and R. Morris. Etna: A fault-tolerant algorithm for atomic mutable DHT data. Technical Report MIT-LCS-TR-993, MIT-LCS, June 2005.
[13]: D. Neel. Cogent, Level 3 in standoff over Internet access. TechWeb, Oct. 2005.
[14]: V. Paxson. Measurements and Analysis of End-to-End Internet Dynamics. PhD thesis, U.C. Berkeley, 1997.
[15]: P. Pietzuch, J. Ledlie, and M. Seltzer. Supporting network coordinates on PlanetLab. 2005.
[16]: S. Rhea. OpenDHT: A public DHT service. PhD thesis, U.C. Berkeley, Aug. 2005.
[17]: S. Rhea, B.-G. Chun, J. Kubiatowicz, and S. Shenker. Fixing the embarrassing slowness of OpenDHT on PlanetLab. In Proc. WORLDS, Dec. 2005.
[18]: S. Rhea, D. Geels, T. Roscoe, and J. Kubiatowicz. Handling churn in a DHT. In USENIX Annual Tech. Conf., June 2004.
[19]: S. Rhea, B. Godfrey, B. Karp, J. Kubiatowicz, S. Ratnasamy, S. Shenker, I. Stoica, and H. Yu. OpenDHT: A public DHT service and its uses. In Proc. SIGCOMM, Aug. 2005.
[20]: R. Rodrigues and B. Liskov. Rosebud: A scalable byzantine-fault-tolerant storage architecture. Technical Report TR/932, MIT CSAIL, Dec. 2003.
[21]: A. Rowstron and P. Druschel. Pastry: Scalable, distributed object location and routing for large-scale peer-to-peer systems. In Proc. IFIP/ACM Middleware, Nov. 2001.
[22]: I. Stoica, D. Adkins, S. Zhuang, S. Shenker, and S. Surana. Internet Indirection Infrastructure. In Proc. SIGCOMM, Aug. 2002.
[23]: I. Stoica, R. Morris, D. Karger, M. F. Kaashoek, and H. Balakrishnan. Chord: A scalable peer-to-peer lookup service for Internet applications. In Proc. SIGCOMM, Aug. 2001.

Footnotes:

¹For some applications, link-state routing may in fact be the right solution, but such systems are outside the scope of our consideration.

²We note, however, that neither of our Vivaldi implementations include the kinds of filtering used by Pietzuch, Ledlie, and Seltzer to produce more accurate coordinates on PlanetLab [15]; it is possible that their implementation would produce more accurate timeout values.

³A similar approach, where R uses the DHT's routing algorithm to route its response to S's identifier, has a similar cost but a lower likelihood of success in most cases, so we ignore it here.

⁴DHash actually stores erasure codes rather than replicas, but the distinction is not relevant to this discussion.