NSDI '06 Paper
[NSDI '06 Technical Program]
Efficient Replica Maintenance for Distributed
Storage Systems
Byung-Gon
Chun,† Frank
Dabek,⋆ Andreas
Haeberlen,‡ Emil
Sit,⋆ Hakim
Weatherspoon,†
M. Frans Kaashoek,⋆ John
Kubiatowicz,† and Robert
Morris⋆
⋆ MIT Computer
Science and Artificial Intelligence
Laboratory,
‡
Rice University/MPI-SWS,
† University of
California, Berkeley
|
Abstract
This paper considers replication
strategies for storage systems that aggregate the disks of many
nodes spread over the Internet. Maintaining replication in such
systems can be prohibitively expensive, since every transient
network or host failure could potentially lead to copying a
server's worth of data over the Internet to maintain replication
levels.
The following insights in designing an efficient replication
algorithm emerge from the paper's analysis. First, durability can
be provided separately from availability; the former is less
expensive to ensure and a more useful goal for many wide-area
applications. Second, the focus of a durability algorithm must be
to create new copies of data objects faster than permanent disk
failures destroy the objects; careful choice of policies for what
nodes should hold what data can decrease repair time. Third,
increasing the number of replicas of each data object does not help
a system tolerate a higher disk failure probability, but does help
tolerate bursts of failures. Finally, ensuring that the system
makes use of replicas that recover after temporary failure is
critical to efficiency.
Based on these insights, the paper proposes the
Carbonite replication algorithm for keeping data durable at a low
cost. A simulation of Carbonite storing 1 TB of data over a 365 day
trace of PlanetLab activity shows that Carbonite is able to keep all
data durable and uses 44% more network traffic than a hypothetical
system that only responds to permanent failures. In comparison,
Total Recall and DHash require almost a factor of two more network
traffic than this hypothetical system.
1 Introduction
Wide-area
distributed storage systems typically use replication to provide
two related properties: durability and availability.
Durability means that objects that an application has
put into the system are not lost due to disk failure
whereas availability means that get will be able
to return the object promptly. Objects can be durably stored but
not immediately available: if the only copy of an object is on the
disk of a node that is currently powered off, but will someday
re-join the system with disk contents intact, then that object is
durable but not currently available. The paper's goal is to develop
an algorithm to store immutable objects durably and at a low
bandwidth cost in a system that aggregates the disks of many
Internet nodes.
The threat to durability is losing the last copy of an object
due to permanent failures of disks. Efficiently countering this
threat to durability involves three main challenges. First, network
bandwidth is a scarce resource in a wide-area distributed storage
system. To store objects durably, there must be enough network
capacity to create copies of objects faster than they are lost due
to disk failure. Second, a system cannot always distinguish between
transient failures and permanent disk failures: it may waste
network bandwidth by creating new copies during transient failures.
Third, after recovery from transient failures, some replicas may be
on nodes that the replica lookup algorithm does not query and are
thus effectively lost.
Since transient failures are common in wide-area systems,
replication algorithms can waste bandwidth by making unneeded
replicas. For example, the initial replication
algorithm [6] that
the DHash distributed hash table (DHT) [9] turned out to be inadequate
to build storage applications such as UsenetDHT [34], Antiquity [11], and
OverCite [35, 36].
A problem with DHash was that its design was driven by the goal
of achieving 100% availability; this decision caused it to waste
bandwidth by creating new replicas in response to temporary
failures. Its design and similar ones (such as Total
Recall [3])
are overkill for durability. Furthermore, users of many Internet
applications can tolerate some unavailability. For example, Usenet
readers will see all articles eventually, as long as they are
stored durably. Our experience with these DHT applications has led
us to the following insights:
- Durability is a more practical and useful
goal than availability for applications that store objects (as
opposed to caching objects).
- The main goal of a durability algorithm
should be to create new copies of an object faster than they are
destroyed by disk failures; the choice of how replicas are
distributed among nodes can make this task easier.
- Increasing the replication level does not
help tolerate a higher average permanent failure rate, but it does
help cope with bursts of failures.
- Reintegrating returning replicas is key to
avoiding unnecessary copying.
Using these insights we have developed Carbonite, an efficient
wide-area replication algorithm for keeping objects durable. After
inserting a set of initial replicas, Carbonite begins by creating
new replicas mostly in response to transient failures. However,
over time it is increasingly able to ignore transient failures and
approaches the goal of only producing replicas in response to
permanent failures.
Carbonite's design assumes that the disks in the distributed
storage system fail independently of each other: failures of
geographically distributed hard drives from different manufacturers
are likely to be uncorrelated.
In a year-long PlanetLab failure trace, however, we observe some
correlated failures because of coordinated re-installs of the
PlanetLab software. Despite this, an evaluation using the PlanetLab
failure trace shows that Carbonite is able to keep 1 TB of data
durable, and consumes only 44% more network traffic than a
hypothetical system that only responds to permanent failures. In
comparison, Total Recall and DHash require almost a factor of two
more network traffic than this hypothetical system.
The rest of this paper explains our durability models and
algorithms, interleaving evaluation results into the explanation.
Section 2 describes the
simulated evaluation environment. Section 3 presents a model of the relationship
between network capacity, amount of replicated data, number of
replicas, and durability. Section 4
explains how to decrease repair time, and thus increase durability,
by proper placement of replicas on servers. Section 5 presents an algorithm that reduces the bandwidth
wasted making copies due to transient failures.
Section 6 outlines some of the
challenges that face practical implementations of these ideas,
Section 7 discusses related work,
and Section 8 concludes.
2 System environment
The behavior of
a replication algorithm depends on the environment in which it is
used: high disk failure rates or low network access link speeds
make it difficult for any system to maintain durability. We will
use the characteristics of the PlanetLab testbed as a
representative environment when evaluating wide-area replication
techniques. For explanatory purposes, we will also use a synthetic
trace that makes some of the underlying trends more visible. This
section describes both environments, as well as the simulator we
used to evaluate our algorithm.
2.1 PlanetLab characteristics
PlanetLab is a large
(> 600 node) research testbed [28] with nodes located around the
world. We chose this testbed as our representative environment
mainly because it is a large, distributed collection of machines
that has been monitored for long periods; we use this monitoring
data to construct a realistic trace of failures in a mostly managed
environment.
The main characteristics of PlanetLab that interest us are the
rates of disk and transient failures. We use historical data
collected by the CoMon project [25] to identify transient failures.
CoMon has archival records collected on average every 5 minutes
that include the uptime as reported by the system uptime counter on
each node. We use resets of this counter to detect reboots, and we
estimate the time when the node became unreachable based on the
last time CoMon was able to successfully contact the node. This
allows us to pinpoint failures without depending on the
reachability of the node from the CoMon monitoring site.
We define a disk failure to be any permanent loss of disk
contents, due to disk hardware failure or because its contents are
erased accidentally or intentionally. In order to identify disk
failures, the CoMon measurements were supplemented with event logs
from PlanetLab Central [28]. This database automatically
records each time a PlanetLab node is reinstalled (e.g., for an
upgrade, or after a disk is replaced following a failure). The
machine is then considered offline until the machine is assigned a
regular boot state in the database. Table 1 summarizes the statistics of this trace.
Figure 7(a) visualizes how
transient and disk failures accumulate over time in this
network.
| Dates |
1 March 2005 – 28 Feb
2006 |
| Number of hosts |
632 |
| Number of transient failures |
21255 |
| Number of disk failures |
219 |
| Transient host downtime (s) |
1208, 104647, 14242 |
| Any failure interarrival (s) |
305, 1467, 3306 |
| Disk failures interarrival
(s) |
54411, 143476, 490047 |
| (Median/Mean/90th
percentile) |
Table 1: CoMon+PLC trace characteristics.
2.2 Synthetic trace
We also
generated synthetic traces of failures by drawing failure
inter-arrival times from exponential distributions. Synthetic
traces have two benefits. First, they let us simulate longer time
periods, and second, they allow us to increase the failure density,
which makes the basic underlying trends more visible. We conjecture
that exponential inter-failure times are a good model for disks
that are independently acquired and operated at geographically
separated sites; exponential intervals are possibly not so well
justified for transient failures due to network problems.
Each synthetic trace contains 632 nodes, just like the PlanetLab
trace. The mean session time and downtime match the values shown in
Table 1; however, in order to
increase the failure density, we extended the length to two years
and reduced the average node lifetime to one year. Each experiment
was run with ten different traces; the figures show the averages
from these experiments.
2.3 Simulation
We
use the failure traces to drive an event-based simulator. In the
simulator, each node has unlimited disk capacity, but limited link
bandwidth. However, it assumes that all network paths are
independent so that there are no shared bottlenecks. Further it
assumes that if a node is available, it is reachable from all other
nodes. This is occasionally not the case on
PlanetLab [14];
however, techniques do exist to mask the effects of partially
unreachable nodes [1].
The simulator takes as input a trace of transient and disk
failure events, node repairs and object insertions. It simulates
the behavior of nodes under different protocols and produces a
trace of the availability of objects and the amount of data sent
and stored by each node for each hour of simulated time. Each
simulation calls put with 50,000 data objects, each of
size 20 MB. Unless otherwise noted, each node is configured with an
access link capacity of 150 KBytes/s, roughly corresponding to the
throughput achievable under the bandwidth cap imposed by PlanetLab.
The goal of the simulations is to show the percentage of objects
lost and the amount of bandwidth needed to sustain objects over
time.
3 Understanding durability
We consider the
problem of providing durability for a storage system composed of a
large number of nodes spread over the Internet, each contributing
disk space. The system stores a large number of independent pieces
of data. Each piece of data is immutable. The system must have a
way to name and locate data; the former is beyond the scope of this
work, while the latter may affect the possible policies for placing
replicas. While parts of the system will suffer temporary failures,
such as network partitions or power failures, the focus of this
section is on failures that result in permanent loss of data.
Section 5 shows how to efficiently
manage transient failures; this section describes some fundamental
constraints and challenges in providing durability.
3.1 Challenges to durability
It is useful to view permanent disk and node failures as having an
average rate and a degree of burstiness. To provide high
durability, a system must be able to cope with both.
In order to handle some average rate of failure, a
high-durability system must have the ability to create new replicas
of objects faster than replicas are destroyed. Whether the system
can do so depends on the per-node network access link speed, the
number of nodes (and hence access links) that help perform each
repair, and the amount of data stored on each failed node. When a
node n fails, the other nodes holding replicas of the
objects stored on n must generate replacements: objects will
remain durable if there is sufficient bandwidth available on
average for the lost replicas to be recreated. For example, in a
symmetric system each node must have sufficient bandwidth to copy
the equivalent of all data it stores to other nodes during its
lifetime.
If nodes are unable to keep pace with the average failure rate,
no replication policy can prevent objects from being lost. These
systems are infeasible. If the system is infeasible, it
will eventually “adapt” to the failure rate by
discarding objects until it becomes feasible to store the remaining
amount of data. A system designer may not have control over access
link speeds and the amount of data to be stored; fortunately,
choice of object placement can improve the speed that a system can
create new replicas as discussed in Section 4.
If the creation rate is only slightly above the average failure
rate, then a burst of failures may destroy all of an object's
replicas before a new replica can be made; a subsequent lull in
failures below the average rate will not help replace replicas if
no replicas remain. For our purposes, these failures are
simultaneous: they occur closer together in time than the
time required to create new replicas of the data that was stored on
the failed disk. Simultaneous failures pose a constraint tighter
than just meeting the average failure rate: every object must have
more replicas than the largest expected burst of failures. We study
systems that aim to maintain a target number of replicas in order
to survive bursts of failure; we call this target
rL.
Higher values of rL do not allow
the system to survive a higher average failure rate. For examples,
if failures were to arrive at fixed intervals, then either
rL=2 would always be sufficient, or no
amount of replication would ensure durability. If
rL = 2 is sufficient, there will always be
time to create a new replica of the objects on the most recently
failed disk before their remaining replicas fail. If creating new
replicas takes longer than the average time between failures, no
fixed replication level will make the system feasible; setting a
replication level higher than two would only increase the number of
bytes each node must copy in response to failures, which is already
infeasible at rL=2.
3.2 Creation versus failure rate
It might seem that any creation rate higher than the average
failure rate will lead to an unbounded number of replicas, thus
satisfying the burst constraint. However, this intuition is false.
To see why, let us model the number of replicas of an object as a
birth-death process using a continuous time Markov chain, which
assumes independent exponential inter-failure and inter-repair
times. This assumption is reasonable for independent disk failures.

Figure 1: A continuous time Markov model for
the process of replica failure and repair for a system that
maintains three replicas ( rL=3). Numbered
states correspond to the number of replicas of each object that are
durable. Transitions to the left occur at the rate at which
replicas are lost; right-moving transitions happen at the replica
creation rate.
An object is in state i when i disks hold a replica
of the object. There are thus rL + 1
possible states, as we start with rL
replicas and only create new replicas in response to failures. From
a given state i, there is a transition to state i+1
with rate μi corresponding to repair, except
for state 0 which corresponds to loss of durability and state
rL which does not need repair. The actual
rate μi depends on how bandwidth is allocated
to repair and may change depending on the replication level of an
object. There is a transition to the next lower state
i−1 with rate iλf
because each of the i nodes holding an existing replica
might fail. Figure 1 shows this
model for the case where rL = 3.
This model can be analyzed numerically to shed light on the
impact of rL on the probability of data
loss; we will show this in Section 3.3. However, to gain some intuition about the
relationship between creation and failure rates and the impact this
has on the number of replicas that can be supported, we consider a
simplification of Figure 1 that
uses a fixed μ but repairs constantly, even allowing for
transitions out of state 0. While these changes make the model less
realistic, they turn the model into an M/M/∞
queue [19]
where the “arrival rate” is the repair rate and the
“service rate” is the per-replica failure rate. The
“number of busy servers” is the number of replicas: the
more replicas an object has, the more probable it is that one of
them will fail.
This simplification allows us to estimate the equilibrium number
of replicas: it is μ/λf. Given μ and
λf, a system cannot expect to support more
than this number of replicas. For example, if the system must
handle coincidental bursts of five failures, it must be able to
support at least six replicas and hence the replica creation rate
must be at least 6 times higher than the average replica failure
rate. We will refer to μ/λf as θ.
Choices for rL are effectively limited by
θ. It is not the case that durability increases continuously
with rL; rather, when using
rL > θ, the system provides the
best durability it can, given its resource constraints. Higher
values of θ decrease the time it takes to repair an object,
and thus the `window of vulnerability' during which additional
failures can cause the object to be destroyed.
To get an idea of a real-world value of θ, we estimate
μ and λf from the historical failure
record for disks on PlanetLab. From Table 1, the average disk failure inter-arrival time
for the entire test bed is 39.85 hours. On average, there were
490 nodes in the system, so we can estimate the mean time
between failures for a single disk as 490⋅ 39.85 hours or
2.23 years. This translates to λf
≈ 0.439 disk failures per year.
The replica creation rate μ depends on the achievable network
throughput per node, as well as the amount of data that each node
has to store (including replication). PlanetLab currently limits
the available network bandwidth to 150 KB/s per node, and if we
assume that the system stores 500 GB of unique data per node with
rL = 3 replicas each, then each of the
490 nodes stores 1.5 TB. This means that one node's data can
be recreated in 121 days, or approximately three times per
year. This yields μ ≈ 3 disk copies per year.
In a system with these characteristics, we can estimate θ
= μ/λf ≈ 6.85, though the actual
value is likely to be lower. Note that this ratio represents the
equilibrium number of disks worth of data that can be
supported; if a disk is lost, all replicas on that disk are lost.
When viewed in terms of disk failures and copies, θ depends
on the value of rL: as
rLincreases, the total amount of data
stored per disk (assuming available capacity) increases
proportionally and reduces μ. If λf =
μ, the system can in fact maintain
rLreplicas of each object.
To show the impact of θ, we ran an experiment with the
synthetic trace (i.e., with 632 nodes, a failure rate of
λf = 1 per year and a storage load of 1
TB), varying the available bandwidth per node. In this case, 100
B/s corresponds to θ=1.81 / rL.
Figure 2 shows that, as θ drops
below one, the system can no longer maintain full replication and
starts operating in a `best effort' mode, where higher values of
rL do not give any benefit. The exception
is if some of the initial rL replicas
survive through the entire trace, which explains the small
differences on the left side of the graph.
Figure 2: Average number of replicas per object
at the end of a two-year synthetic trace for varying values of
θ, which varies with bandwidth per node (on the
x-axis) and total data stored (rL).
Where θ < 1, the system cannot maintain the full
replication level; increasing rL further
does not have any effect.
3.3 Choosing
rL
Figure 3: Frequency of
“simultaneous” failures in the PlanetLab trace. These
counts are derived from breaking the trace into non-overlapping 24
and 72 hour periods and noting the number of permanent failures
that occur in each period. If there are x replicas of an
object, there were y chances in the trace for the object to
be lost; this would happen if the remaining replicas were not able
to respond quickly enough to create new replicas of the
object.
A system designer must choose an appropriate value of
rLto meet a target level of durability.
That is, for a given deployment environment,
rLmust be high enough so that a burst of
rL failures is sufficiently rare.
One approach is to set rLto one more
than the maximum burst of simultaneous failures in a trace of a
real system. For example, Figure 3
shows the burstiness of permanent failures in the PlanetLab trace
by counting the number of times that a given number of failures
occurs in disjoint 24 hour and 72 hour periods. If the size of a
failure burst exceeds the number of replicas, some objects may be
lost. From this, one might conclude that 12 replicas are needed to
maintain the desired durability. This value would likely provide
durability but at a high cost. If a lower value of
rLwould suffice, the bandwidth spent
maintaining the extra replicas would be wasted.
There are several factors to consider in choosing
rLto provide a certain level of
durability. First, even if failures are independent, there is a
non-zero (though small) probability for every burst size up to the
total number of nodes. Second, a burst may arrive while there are
fewer than rLreplicas. One could conclude
from these properties that the highest possible value of
rLis desirable. On the other hand, the
simultaneous failure of even a large fraction of nodes may not
destroy any objects, depending on how the system places replicas
(see Section 4). Also, the workload
may change over time, affecting μ and thus θ.
The continuous time Markov model described in
Figure 1 reflects the
distributions of both burst size and object replication level. The
effect of these distributions is significant. An analysis of the
governing differential equations can be used to derive the
probability that an object will be at a given replication level
after a given amount of time. In particular, we can determine the
probability that the chain is in state 0, corresponding to a loss
of durability.
We show the results of such an analysis in Figure 4; for details, see [7]. To explore different workloads,
we consider different amounts of data per node. The graph shows the
probability that an object will survive after four years as a
function of rL and data stored per node
(which affects the repair rate and hence θ).
As rL increases, the system can
tolerate more simultaneous failures and objects are more likely to
survive. The probability of object loss at
rL=1 corresponds to using no replication.
This value is the same for all curves since it depends only on the
lifetime of a disk; no new replicas can be created once the only
replica of the object is lost. To store 50 GB durably, the system
must use an rL of at least 3. As the total
amount of data increases, the rL required
to attain a given survival probability also increases. Experiments
confirm that data is lost on the PlanetLab trace only when
maintaining fewer than three replicas.

Figure 4: Analytic prediction for object
durability after four years on PlanetLab. The x-axis shows
the initial number of replicas for each object: as the number of
replicas is increased, object durability also increases. Each curve
plots a different per-node storage load; as load increases, it
takes longer to copy objects after a failure and it is more likely
that objects will be lost due to simultaneous failures.
4 Improving repair time
This section explores how
the system can increase durability by replacing replicas from a
failed disk in parallel. In effect, this reduces the time needed to
repair the disk and increases θ.
Each node, n, designates a set of other nodes that can
potentially hold copies of the objects that n is responsible
for. We will call the size of that set the node's scope, and
consider only system designs in which every node has the same
scope. Scope can range from a minimum of
rL to a maximum of the number of nodes in
the system.
A small scope means that all the objects stored on node n
have copies on nodes chosen from the same restricted set of other
nodes. The advantage of a small scope is that it makes it easier to
keep track of the copies of each object. For example, DHash stores
the copies of all the objects with keys in a particular range on
the successor nodes of that key range; the result is that those
nodes store similar sets of objects, and can exchange compressed
summaries of the objects they store when they want to check that
each object is replicated a sufficient number of
times [6].
The disadvantage of a small scope is that the effort of creating
new copies of objects stored on a failed disk falls on the small
set of nodes in that disk's scope. The time required to create the
new copies is proportional to the amount of data on one disk
divided by the scope. Thus a small scope results in a long recovery
time. Another problem with a small scope, when coupled with
consistent hashing, is that the addition of a new node may cause
needless copying of objects: the small scope may dictate that the
new node replicate certain objects, forcing the previous replicas
out of scope and thus preventing them from contributing to
durability.
Larger scopes spread the work of making new copies of objects on
a failed disk over more access links, so that the copying can be
completed faster. In the extreme of a scope of N (the number
of nodes in the system), the remaining copies of the objects on a
failed disk would be spread over all nodes, assuming that there are
many more objects than nodes. Furthermore, the new object copies
created after the failure would also be spread over all the nodes.
Thus the network traffic sources and destinations are spread over
all the access links, and the time to recover from the failure is
short (proportional to the amount of data on one disk divided by
N).
A larger scope also means that a temporary failure will be
noticed by a larger number of nodes. Thus, more access links are
available to create additional replicas while the failure lasts.
Unless these links are already fully utilized, this increases the
effective replica creation rate, and thus improves durability.
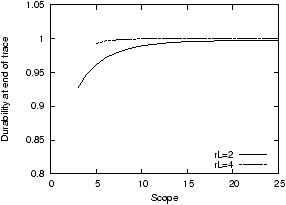
Figure 5: Durability for different scopes in a
synthetic trace with low θ. Larger scopes spread the repair
work over more access links and improve the nodes' ability to
monitor replicas and temporary failures, which results in higher
durability.
Figure 5 shows how scope (and
thus repair time) affects object durability in a simulation on a
synthetic trace. To reduce θ, we limit the bandwidth per node
to 1000 B/s in this experiment. We vary the repair threshold and
the scope, and measure durability after two years of simulated
time. Increasing the scope from 5 to 25 nodes reduces the fraction
of lost objects by an order of magnitude, independent of
rL. By including more nodes (and thus more
network connections) in each repair effort, the work is spread over
more access links and completes faster, limiting the window of time
in which the system is vulnerable to another disk failure. Ideally,
by doubling the scope, the window of vulnerability can be cut in
half.
A large scope reduces repair time and increases durability;
however, implementing a large scope presents two trade-offs. First,
the system must monitor each node in the scope to determine the
replication levels; when using a large scope, the system must
monitor many nodes. This increased monitoring traffic limits
scalability. Second, in some instances, a large scope can increase
the likelihood that a simultaneous failure of multiple disks will
cause some object to be lost.
If objects are placed randomly with scope N and there are
many objects, then it is likely that all
NCrL
potential replica sets are used. In this scenario, the
simultaneous failure of any rL disks is
likely to cause data loss: there is likely to be at least one
object replicated on exactly those disks. A small scope limits
placement possibilities that are used, concentrating objects into
common replica sets. As a result, it is less likely that a given
set of rL failures will affect a replica
set, but when data loss does occur, many more objects will be lost.
These effects exactly balance: the expected number of objects lost
during a large failure event is identical for both strategies. It
is the variance that differs between the two strategies.
5 Reducing transient costs
The possibility of
transient failures complicates providing durability efficiently: we
do not want to make new copies in response to transient failures,
but it is impossible to distinguish between disk failures and
transient failures using only remote network measurements. This
section focuses minimizing the amount of network traffic sent in
response to transient failures.
The key technique needed to achieve this is to ensure that the
system reintegrates object replicas stored on nodes after transient
failures; this means the system must be able to track more than
rL replicas of each object. The number of
replicas that the system must remember turns out to be dependent on
a, the average fraction of time that a node is available.
However, we show that the correct number of extra replicas can be
determined without estimating a by tracking the location of
all replicas, including those that are offline. We introduce the
Carbonite algorithm that uses this technique and demonstrate its
effectiveness using simulations.
We additionally consider two other techniques for limiting
response to transient failures: creating extra replicas in batches
and using timeouts as a heuristic for distinguishing transient from
disk failures. Both are of limited value: batching is best able to
save bandwidth when using erasure codes and, in the presence of
reintegration, timeouts work well only if node downtimes are
notably shorter than node (and disk) lifetimes.
5.1 Carbonite details
The Carbonite maintenance algorithm focuses on reintegration to
avoid responding to transient failures. Durability is provided by
selecting a suitable value of rL; an
implementation of Carbonite should place objects to maximize θ
and preferentially repair the least replicated object. Within these
settings, Carbonite works to efficiently maintain
rLcopies, thus providing durability.
Because it is not possible to distinguish between transient and
disk failures remotely, Carbonite simply responds to any detected
failure by creating a new replica. This approach is shown in
Figure 6. If fewer than
rL replicas are detected as available, the
algorithm creates enough new replicas to return the replication
level to rL.
// Iterate through the object database
// and schedule an object for repair if needed
Maintain_Replicas ()
keys = <DB.object_keys sorted number of available replicas>
foreach k in keys:
n = replicas[k].len ()
if n < rL:
newreplica = enqueue_repair (k)
replicas[k].append (newreplica)
Figure 6: Each node maintains a list of objects
for which it is responsible and monitors the replication level of
each object using some synchronization mechanism. In this code,
this state is stored in the replicas hash table though an
implementation may choose to store it on disk. This code is called
periodically to enqueue repairs on those objects that have too few
replicas available; the application can issue these requests at its
convenience.
However, Carbonite remembers which replicas were stored on nodes
that have failed so that they can be reused if they return. This
allows Carbonite to greatly reduce the cost of responding to
transient failures. For example, if the system has created two
replicas beyond rL and both fail, no work
needs to be done unless a third replica fails before one of the two
currently unavailable replicas returns. Once enough extra replicas
have been created, it is unlikely that fewer than
rL of them will be available at any given
time. Over time, it is increasingly unlikely that the system will
need to make any more replicas.
5.2 Reintegration reduces maintenance
Figure 7: A comparison of the total amount of
work done by different maintenance algorithms with
rL=3 using a PlanetLab trace (left) and a
synthetic trace (right). In all cases, no objects are lost.
However, rL = 2 is insufficient: for the
PlanetLab trace, even a system that could distinguish permanent
from transient failures would lose several objects.
Figure 7 shows the importance
of reintegrating replicas back into the system by comparing the
behavior of Carbonite to two prior DHT systems and a hypothetical
system that can differentiate disk from transient failures using an
oracle and thus only reacts to disk failures. In the simulation,
each system operates with rL=3. The
systems are simulated against the PlanetLab trace (a) and a
synthetic trace (b). The y-axes plot the cumulative number
of bytes of network traffic used to create replicas; the
x-axes show time.
Unlike all other synthetic traces used in this paper, whose
parameters are different from the PlanetLab trace in order to bring
out the basic underlying trends, the synthetic trace used in
Figure 7 was configured to be
similar to the PlanetLab trace. In particular, the average node
lifetime and the median downtime are the same. The result is still
an approximation (for example, PlanetLab grew during the trace) but
the observed performance is similar. Some of the observed
differences are due to batching (used by Total Recall) and timeouts
(used by all systems); the impact of these are discussed in more
detail in Sections 5.4 and
5.5.
Since the oracle system responds only to disk failures, it uses
the lowest amount of bandwidth. The line labeled Cates shows a
system that keeps track of exactly rL
replicas per object; this system approximates the behavior of DHTs
like DHash, PAST and OpenDHT. Each failure causes the number of
replicas to drop below rL and causes this
system to create a new copy of an object, even if the failure was
transient. If the replica comes back online, it is discarded. This
behavior results in the highest traffic rate shown. The difference
in performance between the PlanetLab and Poisson trace is due to
differences in the distribution of downtimes: Poisson is not a
particularly good fit for the PlanetLab downtime distribution.
Total Recall [3] tracks up to a fixed
number of replicas, controlled by a parameter
rH; we show rH =
5 which is optimal for these traces, and
rH = 9. As can be seen at the right of the
graphs, this tracking of additional replicas allows Total Recall to
create fewer replicas than the Cates system. When more than
rL replicas are available, a transient
failure will not cause Total Recall to make a new copy. However,
Total Recall's performance is very sensitive to
rH. If rH is set
too low, a series of transient failures will cause the replication
level to drop below rL and force it to
create an unnecessary copy. This will cause Total Recall to
approach Cates (when rH =
rL). Worse, when the system creates new
copies it forgets about any copies that are currently on failed
nodes and cannot benefit from the return of those copies. Without a
sufficiently long memory, Total Recall must make additional
replicas. Setting rHtoo high imposes a
very high insertion cost and results in work that may not be needed
for a long time.
Carbonite reintegrates all returning replicas into the replica
sets and therefore creates fewer copies than Total Recall. However,
Carbonite's inability to distinguish between transient and disk
failures means that it produces and maintains more copies than the
oracle based algorithm. This is mainly visible in the first weeks
of the trace as Carbonite builds up a buffer of extra copies. By the
end of the simulations, the rate at which Carbonite produces new
replicas approaches that of the oracle system.
5.3 How many replicas?
To formalize our intuition about the effect of extra replicas on
maintenance cost and to understand how many extra replicas are
necessary to avoid triggering repair following a transient failure,
consider a simple Bernoulli process measuring R, the number
of replicas available at a given moment, when there are
r>rL total replicas. The
availability of each node is a. Since repair is triggered
when the number of available replicas is less than
rL, the probability that a new replica
needs to be created is the probability that less than
rL replicas are available:
| Pr[R < rL
| r extant copies |
] = |
|
|
ai (1 −
a)r − i. |
This probability falls rapidly as r increases but it will
never reach zero; there is always a chance that a replica must be
created due to a large number of concurrent failures, regardless of
how many replicas exist already. However, when a large number of
replicas exists, it is extremely unlikely that enough replicas fail
such that fewer than rL are available.
By computing the Chernoff bound, it is possible to show that
after the system has created 2rL/a
replicas, the probability of a new object creation is exponentially
small. 2rL/a is a rough (and
somewhat arbitrary) estimate of when the probability of a new
object creation is small enough to ignore. Figure 8 shows (on the y-axis) the
probability that a new object must be created when an increasing
number of replicas already exist. As r increases, the
probability that a new replica needs to be created falls, and the
algorithm creates replicas less frequently. As r approaches
2rL/a, the algorithm essentially
stops creating replicas, despite not knowing the value of
a.

Figure 8: Additional redundancy must be created
when the amount of live redundancy drops below the desired amount
(3 replicas in this example). The probability of this happening
depends solely on the average node availability a and the
amount of durable redundancy. This graph shows the probability of a
repair action as a function of the amount of durable redundancy,
with a = 0.5, a = 0.7 and a = 0.9 for a
replication system.
This benefit is obtained only if returning replicas are
reintegrated into the appropriate replica set, allowing more than
rL to be available with high probability.
As a result, the cost of responding to transient failures will be
nearly zero. Still, this system is more expensive than an oracle
system that can distinguish between disk and transient failures.
While the latter could maintain exactly rL
replicas, the former has to maintain approximately
2rL/a. The factor of 2/a
difference in the cost is the penalty for not distinguishing disk
and transient failures.
5.4 Create replicas as needed
Given that the system
tends towards creating 2rL/a
replicas in order to keep rL of them
available, it is tempting to create the entire set—not just
rL of them—when the object is first
inserted into the system (Total Recall [3] uses a similar
technique). However, this approach requires an accurate estimate
for a to deliver good performance. If a is
overestimated, the system quickly finds itself with less than
rL replicas after a string of transient
failures and is forced to create additional copies. If a is
underestimated, the system creates unneeded copies and wastes
valuable resources. Carbonite is simplified by the fact that it does
not need to measure or estimate a to create the
“correct” number of replicas.
Another idea is to create not only enough copies to bring the
number of available replicas back up to
rL, but also e additional copies
beyond rL (this is similar to Total
Recall's lazy repair technique). Creating a batch of copies makes
repair actions less frequent, but at the same time, causes more
maintenance traffic than Carbonite. The work required to create
additional replicas will be wasted if those replicas are lost due
to disk failures before they are actually required. Carbonite, on
the other hand, only creates replicas that are necessary to keep
rL replicas available. In other words,
either Carbonite would eventually create the same number of
replicas as a scheme that creates replicas in batches, or some
replicas created in the batch were unnecessary: batch schemes do,
at best, the same amount of work as Carbonite.
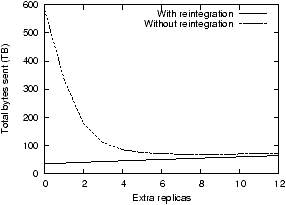
Figure 9: Total repair cost with extra
replicas, and with and without reintegration after repair. Without
reintegration, extra replicas reduce the rate at which repair is
triggered and thus reduce maintenance cost; there is an optimal
setting (here e=8). With reintegration, the cost is lowest
if no extra replicas are used.
Figure 9 shows the bytes
sent in a simulation experiment using a five-year synthetic trace
with a=0.88, rL=3, and an average
node lifetime of one year. The graph shows results for different
values of e (in Total Recall, e =
rH − rL)
and for two different scenarios. In the scenario with
reintegration, the system reintegrates all replicas as they return
from transient failures. This scenario represents the behavior of
Carbonite when e=0 and causes the least traffic.
In the scenario without reintegration, replicas that are
unavailable when repair is triggered are not reintegrated into the
replica set even if they do return. Total Recall behaves this way.
Extra replicas give the system a short-term memory. Additional
replicas increase the time until repair must be made (at which time
failed replicas will be forgotten); during this time failed
replicas can be reintegrated. Larger values of e give the
system a longer memory but also put more data at risk of failure:
on this synthetic trace, a value of e=8 is optimal. Taking
advantage of returning replicas is simpler and more efficient than
creating additional replicas: a system that reintegrates returning
replicas will always make fewer copies than a system that does not
and must replace forgotten replicas.
For systems that use erasure codes, there is an additional read
cost since a complete copy of the object is needed in order to
generate a new fragment [32]. The cost of
reading a sufficient number of fragments prior to recreating a lost
fragment can overwhelm the savings that erasure codes provide. A
common approach is to amortize this cost by batching fragment
creation but simply caching the object at the node responsible for
repair is much more effective. A simulation contrasting both
caching and batching (but both with reintegration) shows results
similar to Figure 9:
caching the object with a 7/14 erasure code uses 85% of the
bandwidth that the optimal batching strategy would use.
5.5 Timeouts
A common approach to
reduce transient costs is to use long timeouts, as suggested by
Blake [4]. Timeouts
are a heuristic to avoid misclassifying temporary failures as
permanent: failures are considered to be permanent only when the
corresponding node has not responded for some number of seconds.
Longer timeouts reduce the number of misclassified transient
failures and thus the number of repairs. On the other hand, a
longer timeout also increases the latency between failure and
repair in the event of a true disk failure; if additional permanent
failures occur during this larger “window of
vulnerability,” data may be lost.
The goal of both reintegrating replicas and use of timeouts is
to reduce the number of repairs without decreasing durability.
Figure 7 demonstrates that
reintegration is effective for Carbonite. However, it also
illustrates that timeouts are important in systems without
reintegration: on the PlanetLab trace, the timeout used is able to
mask 87.7% of transient failures whereas it only masks 58.3% of
transient failures on the Poisson trace. If replicas are
reintegrated, what extra benefit does a timeout provide?
Timeouts are most effective when a significant percentage of the
transient failures can be ignored, which is dependent on the
downtime distribution. However, for durability to remain high, the
expected node lifetime needs to be significantly greater than the
timeout.
[] 
[] 
Figure 10: The impact of timeouts on bandwidth
and durability on a synthetic trace. Figure 10(a) shows the number of copies created for various
timeout values; fig10b shows the corresponding object durability.
In this trace, the expected downtime is about 29 hours. Longer
timeouts allow the system to mask more transient failures and thus
reduce maintenance cost; however, they also reduce
durability.
To evaluate this scenario where timeouts should have impact, we
performed an experiment using a synthetic trace where we varied the
repair threshold and the node timeout. Since the system would
recognize nodes returning after a permanent failure and immediately
expire all pending timeouts for these nodes, we assigned new
identities to such nodes to allow long timeouts to expire normally.
Figure 10 shows the
results of this simulation: fig10a shows the total bytes sent as a
function of timeout while fig10b shows the durability at the end of
the trace. As the length of the timeout increases past the average
downtime, we observe a reduction in the number of bytes sent
without a decrease in durability. However, as the timeout grows
longer, durability begins to fall: the long timeout delays the
point at which the system can begin repair, reducing the effective
repair rate. Thus setting a timeout can reduce response to
transient failures but its success depends greatly on its
relationship to the downtime distribution and can in some instances
reduce durability as well.
6 Implementing Carbonite
While the discussion of durability and efficient
maintenance may be broadly applicable, in this section, we focus on
our experience in implementing Carbonite in the context of
distributed hash tables (DHTs).
In a DHT, each node is algorithmically assigned a portion of the
total identifier space that it is responsible for maintaining.
Carbonite requires that each node know the number of available
replicas of each object for which it is responsible. The goal of
monitoring is to allow the nodes to track the number of available
replicas and to learn of objects that the node should be tracking
but is not aware of. When a node n fails the new node
n' that assumes responsibility of n's blocks begins
tracking replica availability; monitored information is soft state
and thus can be failed over to a "successor" relatively
transparently.
Monitoring can be expensive: a node might have to contact every
node in the scope of each object it holds. While developing two
prototype implementations of Carbonite in the PlanetLab
environment, we found it necessary to develop different techniques
for monitoring: the monitoring problem is slightly different in
systems that use distributed directories and those that use
consistent hashing. Figure 11 illustrates the structures of
these systems.
[DHT ] 
[Directory ] 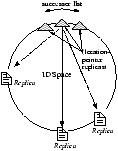
Figure 11: DHT- and Directory- Based Storage
System Architectures.
The Chord/DHash system [8, 9] served as the basis for our
consistent hashing implementation. It uses a small scope and thus
monitors a small number of nodes. DHash does not need to record the
location of failed replicas: a node will return to the same place
in the ring and thus the same replica sets, as long as it returns
with the same logical identifier.
We used Oceanstore [20, 30] and the
BambooDHT [31]
to develop a distributed directory system using large scope and
random placement. Oceanstore must maintain pointers to all nodes
that have ever held data for a given object and has a scope of
N. Responsibility for keys is still assigned using
consistent hashing: the pointer database for each key is replicated
on the successors of the key. In this case, the location of objects
is hard state. Unfortunately, it could be easy for this system to
have very high monitoring costs: if each node communicate with
every other node periodically, the resulting N2
probe traffic may limit the system's scalability.
6.1 Monitoring consistent hashing
systems
In systems that use a small scope, it is possible to make an
end-to-end check that data is stored on the disk of each node. The
naive way to do this is to arrange for nodes to repeatedly exchange
key lists, but such an exchange would be extremely costly.
DHash uses a synchronization protocol based on Merkle
trees [6] that takes
advantage of the fact that most objects are typically correctly
placed. In this common case, adjacent nodes store largely similar
keys and two nodes can exchange a single message (containing a
digest of the stored keys) to verify that they are
synchronized.
Carbonite allows replicas to be placed anywhere in the placement
scope. This flexibility lets the system avoid moving and
replicating objects during most joins (until the system grows
dramatically). However, it also causes the Merkle synchronization
protocol to operate outside of its common case: adjacent nodes are
no longer likely to store nearly identical sets of objects. In this
environment the synchronizer “discovers” that nodes in
the scope are missing objects each time it is run. Repeatedly
exchanging this information can be costly: if the synchronization
protocol runs once a minute, the cost of repeatedly transferring
the 20-byte key of an 8 KB data object will exceed the cost of
transferring the object itself to a newly joined node in about 8
hours.
To avoid this problem, each node maintains, for each object, a
list of nodes in the scope without a copy of the object. The node
uses this information to adjust its Merkle tree to avoid
re-learning the information again during the next run of the
synchronizer. For instance, when a node n synchronizes with
a replica node n' that is known to be missing an object with
key k, n leaves k out of the Merkle tree used
for synchronization: this prevents n' from reporting what
n already knew. The amount of extra state needed to perform
this optimization per object is small relative to the size of
storing the object itself, and can be maintained lazily, unlike the
object itself which is hard state.
6.2 Monitoring host availability
In a directory-style system, the same synchronization techniques
just described can be used to monitor the directory itself (which
is replicated on successor nodes); however, it is likely infeasible
to explicitly monitor the liveness of objects themselves using the
algorithm described above since two nodes are not likely to store
the same keys. Instead, node availability can be monitored as a
proxy for object availability. Node availability can be monitored
using a multicast mechanism that propagates the liveness state of
each node to each other node.
The DHT's routing tables are used to establish a unique spanning
tree rooted at each node a O(logN) out-degree per
node. Each node periodically broadcasts a heartbeat message to its
children in the tree; this message includes a generation identifier
that is randomly generated when the node is installed or
reinstalled following a disk failure. The children rebroadcast the
heartbeat to their children until it is received by all nodes.
Over time, each node expects to receive regular notification of
node liveness. If a heartbeat is missed, the monitoring node
triggers repair for every object stored on the newly down node.
When a node returns and its generation identifier has not changed,
the monitoring node can conclude that objects stored on that node
are again accessible.
7 Related work
7.1 Replication analysis
The use of a birth-death data-loss model is a departure from
previous analyses of reliability. Most DHT evaluations consider
whether data would survive a single event involving the failure of
many nodes [8, 40]. This approach
does not separate durability from availability, and does not
consider the continuous bandwidth consumed by replacing replicas
lost to disk failure.
The model and discussion in this paper is similar to
contemporary work that looks at churn [37] and analyzes the
expected object lifetime [29]. The birth-death
model is a generalization of the calculations that predict the MTBF
for RAID storage systems [26]. Owing to its scale, a
distributed system has more flexibility to choose parameters such
as the replication level and number of replica sets when compared
to RAID systems.
Blake and Rodrigues argue that wide-area storage systems built
on unreliable nodes cannot store a large amount of
data [4]. Their
analysis is based on the amount of data that a host can copy during
its lifetime and mirrors our discussion of feasibility. We come to
a different conclusion because we consider a relatively stable
system membership where data loss is driven by disk failure, while
they assumed a system with continual membership turnover.
The selection of a target replication level for surviving bursts
differs from many traditional fault tolerant storage systems. Such
systems, designed for single-site clusters, typically aim to
continue operating despite some fixed number of failures and choose
number of replicas so that a voting algorithm can ensure correct
updates in the presence of partitions or Byzantine
failures [23,
5, 17, 33, 24].
FAB [33] and
Chain Replication [38] both consider how the
number of possible replicas sets affects data durability. The two
come to opposite conclusions: FAB recommends a small number of
replica sets since more replica sets provide more ways for data to
fail; chain replication recommends many replica sets to increase
repair parallelism and thus reduce repair time. These observations
are both correct: choosing a replica placement strategy requires
balancing the probability of losing some data item during a
simultaneous failure (by limiting the number of replica sets) and
improving the ability of the system to tolerate a higher average
failure rate (by increasing the number of replica sets and
reconstruction parallelism).
Weatherspoon et al [39] studied the increased costs
due to transient failures. Their results quantify the benefits of
maintaining extra replicas in reducing these transient costs.
However, their analysis focuses on systems that forget about extant
replicas that exist when repair is initiated and do not discuss the
benefits of reintegrating them.
7.2 Replicated systems
Replication has been widely used to reduce the risk of data loss
and increase data availability in storage systems (e.g.,
RAID [26], System
R duplex disks [16],
Harp [23], xFS [2], Petal [21], DDS [17], GFS [15]). The algorithms traditionally
used to create and maintain data redundancy are tailored for the
environment in which these systems operate: well-connected hosts
that rarely lose data or become unavailable. As a result they can
maintain a small, fixed number of replicas and create a new replica
immediately following a failure. This paper focuses on wide-area
systems that are bandwidth-limited, where transient network
failures are common, and where it is difficult to tell the
difference between transient failures and disk failures.
Distributed databases [10], online disaster
recovery systems such as Myriad [22], and storage
systems [13, 12, 27] use replication and
mirroring to distribute load and increase durability. These systems
store mutable data and focus on the cost of propagating updates, a
consideration not applicable to the immutable data we assume. In
some cases, data is replicated between a primary and backup sites
and further replicated locally at each site using RAID. Wide area
recovery is initiated only after site failure; individual disk
failure can be repaired locally.
Total Recall is the system most similar to our
work [3]. We
borrow from Total Recall the idea that creating and tracking
additional replicas can reduce the cost of transient failures.
Total Recall's lazy replication keeps a fixed number of replicas
and fails to reincorporate replicas that return after a transient
failure if a repair had been performed. Total Recall also requires
introspection or guessing to determine an appropriate high water
mark that Carbonite can arrive at naturally.
Glacier [18]
is a distributed storage system that uses massive replication to
provide data durability across large-scale correlated failure
events. The resulting tradeoffs are quite different from those of
Carbonite, which is designed to handle a continuous stream of at
small-scale failure events. For example, due to its high
replication level, Glacier can afford very long timeouts and thus
mask almost all transient failures.
8 Conclusions and future work
Inexpensive
hardware and the increasing capacity of wide-area network links
have spurred the development of applications that store a large
amount of data on wide-area nodes. However, the feasibility of
applications based on distributed storage systems is currently
limited by the expense of maintaining data. This paper has
described a set of techniques that allow wide-area systems to
efficiently store and maintain large amounts of data.
These techniques have allowed us to develop and deploy
prototypes of UsenetDHT [34], OverCite [35], and
Antiquity [11]. These systems must
store large amounts of data durably and were infeasible without the
techniques we have presented. In the future, we hope to report on
our long-term experience with these systems.
Acknowledgments
The authors would like to thank Vivek Pai and Aaron Klingaman for
their assistance in compiling the data used for the PlanetLab
traces. This paper has benefited considerably from the comments of
the anonymous reviewers and our shepherd, Larry Peterson.
References
- [1]
- Andersen, D. Improving
End-to-End Availability Using Overlay Networks. PhD thesis,
Massachusetts Institute of Technology, 2004.
- [2]
- Anderson, T. E., Dahlin, M. D.,
Neefe, J. M., Patterson, D. A., Roselli, D. S., and
Wang, R. Y. Serverless network file systems. In
Proc. of the 15th ACM Symposium on Operating System
Principles (Dec. 1995).
- [3]
- Bhagwan, R., Tati, K., Cheng, Y.-C.,
Savage, S., and Voelker, G. M. Total Recall: System
support for automated availability management. In Proc. of the
1st Symposium on Networked Systems Design and Implementation
(Mar. 2004).
- [4]
- Blake, C., and Rodrigues, R. High
availability, scalable storage, dynamic peer networks: Pick two. In
Proc. of the 9th Workshop on Hot Topics in Operating
Systems (May 2003), pp. 1–6.
- [5]
- Castro, M., and Liskov, B.
Practical byzantine fault tolerance and proactive recovery. ACM
Transactions on Computer Systems 20, 4 (2002),
398–461.
- [6]
- Cates, J. Robust and efficient
data management for a distributed hash table. Master's thesis,
Massachusetts Institute of Technology, May 2003.
- [7]
- Dabek, F. A Distributed Hash
Table. PhD thesis, Massachusetts Institute of Technology,
2005.
- [8]
- Dabek, F., Kaashoek, M. F., Karger,
D., Morris, R., and Stoica, I. Wide-area cooperative storage
with CFS. In Proc. of the 18th ACM Symposium on Operating
System Principles (Oct. 2001).
- [9]
- Dabek, F., Li, J., Sit, E., Robertson,
J., Kaashoek, M. F., and Morris, R. Designing a DHT for
low latency and high throughput. In Proc. of the 1st Symposium
on Networked Systems Design and Implementation (Mar.
2004).
- [10]
- Demers, A., Greene, D., Hauser, C.,
Irish, W., Larson, J., Shenker, S., Sturgis, H., Swinehart, D., and
Terry, D. Epidemic algorithms for replicated database
maintenance. In Proc. of the 6th ACM Symposium on Principles of
Distributed Computing (1987), pp. 1–12.
- [11]
- Eaton, P., Weatherspoon, H., and
Kubiatowicz, J. Efficiently binding data to owners in
distributed content-addressable storage systems. In Proc. of
the 3rd International Security in Storage Workshop (Dec.
2005).
- [12]
- EMC. Centera—content
addressed storage system.
https://www.emc.com/products/systems/centera.jsp.
Last accessed March 2006.
- [13]
- EMC. Symmetrix remote data
facility.
https://www.emc.com/products/networking/srdf.jsp.
Last accessed March 2006.
- [14]
- Freedman, M. J., Lakshminarayanan,
K., Rhea, S., and Stoica, I. Non-transitive connectivity and
DHTs. In Proc. of the 2nd Workshop on Real Large Distributed
Systems (Dec. 2005).
- [15]
- Ghemawat, S., Gobioff, H., and Leung,
S.-T. The Google file system. In Proc. of the 2003 19th
ACM Symposium on Operating System Principles (Oct.
2003).
- [16]
- Gray, J., McJones, P., Blasgen, M.,
Lindsay, B., Lorie, R., Price, T., Putzolu, F., and Traiger,
I. The recovery manager of the System R database manager.
ACM Computing Surveys 13, 2 (1981),
223–242.
- [17]
- Gribble, S., Brewer, E., Hellerstein, J.,
and Culler, D. Scalable, distributed data structures for
internet service construction. In Proc. of the 4th Symposium on
Operating Systems Design and Implementation (Oct.
2004).
- [18]
- Haeberlen, A., Mislove, A., and Druschel,
P. Glacier: Highly durable, decentralized storage despite
massive correlated failures. In Proc. of the 2nd Symposium on
Networked Systems Design and Implementation (May
2005).
- [19]
- Kleinrock, L. Queueing
Systems, Volume I: Theory. John Wiley & Sons, Jan.
1975.
- [20]
- Kubiatowicz, J., Bindel, D., Chen, Y.,
Czerwinski, S., Eaton, P., Geels, D., Gummadi, R., Rhea, S.,
Weatherspoon, H., Weimer, W., Wells, C., and Zhao, B.
OceanStore: An architecture for global-scale persistent storage. In
Proc. of the 9th Intl. Conference on Architectural Support for
Programming Languages and Operating Systems (Nov. 2000),
pp. 190–201.
- [21]
- Lee, E. K., and Thekkath,
C. A. Petal: Distributed virtual disks. In Proc. of
the 7th Intl. Conference on Architectural Support for Programming
Languages and Operating Systems (1996),
pp. 84–92.
- [22]
- Leung, S.-T. A., MacCormick, J.,
Perl, S. E., and Zhang, L. Myriad: Cost-effective
disaster tolerance. In Proc. of the 1st USENIX Conference on
File and Storage Technologies (Jan. 2002).
- [23]
- Liskov, B., Ghemawat, S., Gruber, R.,
Johnson, P., Shrira, L., and Williams, M. Replication in the
Harp file system. In Proc. of the 13th ACM Symposium on
Operating System Principles (Oct. 1991),
pp. 226–38.
- [24]
- Litwin, W., and Schwarz, T. LH* RS
: A high-availability scalable distributed data structure using
reed solomon codes. In Proc. of the 2000 ACM SIGMOD Intl.
Conference on Management of Data (May 2000),
pp. 237–248.
- [25]
- Park, K. S., and Pai, V.
CoMon: a mostly-scalable monitoring system for PlanetLab. ACM
SIGOPS Operating Systems Review 40, 1 (Jan. 2006),
65–74.
https://comon.cs.princeton.edu/.
- [26]
- Patterson, D., Gibson, G., and Katz,
R. A case for redundant arrays of inexpensive disks (RAID).
In Proc. of the ACM SIGMOD International Conference on
Management of Data (June 1988).
- [27]
- Patterson, H., Manley, S., Federwisch,
M., Hitz, D., Kleiman, S., and Owara, S. Snapmirror: File
system based asynchronous mirroring for disaster recovery. In
Proc. of the 1st USENIX Conference on File and Storage
Technologies (Jan. 2002).
- [28]
- Peterson, L., Anderson, T., Culler, D.,
and Roscoe, T. A blueprint for introducing disruptive
technology into the Internet. In Proc. of the First ACM
Workshop on Hot Topics in Networks (Oct. 2002).
https://www.planet-lab.org.
- [29]
- Ramabhadran, S., and Pasquale, J.
Analysis of long-running replicated systems. In Proc. of the
25th IEEE Annual Conference on Computer Communications
(INFOCOM) (Apr. 2006).
- [30]
- Rhea, S., Eaton, P., Geels, D.,
Weatherspoon, H., Zhao, B., and Kubiatowicz, J. Pond: the
OceanStore prototype. In Proc. of the 2nd USENIX Conference on
File and Storage Technologies (Apr. 2003).
- [31]
- Rhea, S., Geels, D., Roscoe, T., and
Kubiatowicz, J. Handling churn in a DHT. In Proc. of the
2004 Usenix Annual Technical Conference (June
2004).
- [32]
- Rodrigues, R., and Liskov, B. High
availability in DHTs: Erasure coding vs. replication. In Proc.
of the 4th International Workshop on Peer-to-Peer Systems
(Feb. 2005).
- [33]
- Saito, Y., Froelund, S., Veitch, A.,
Merchant, A., and Spence, S. FAB: building distributed
enterprise disk arrays from commodity components. In Proc. of
the 11th Intl. Conference on Architectural Support for Programming
Languages and Operating Systems (New York, NY, 2004), ACM
Press, pp. 48–58.
- [34]
- Sit, E., Dabek, F., and Robertson,
J. UsenetDHT: A low overhead Usenet server. In Proc. of
the 3rd International Workshop on Peer-to-Peer Systems (Feb.
2004).
- [35]
- Stribling, J., Councill, I. G., Li,
J., Kaashoek, M. F., Karger, D. R., Morris, R., and
Shenker, S. OverCite: A cooperative digital research
library. In Proc. of the 4th International Workshop on
Peer-to-Peer Systems (Feb. 2005).
- [36]
- Stribling, J., Li, J., Councill,
I. G., Kaashoek, M. F., and Morris, R. Exploring
the design of multi-site web services using the OverCite digital
library. In Proc. of the 3rd Symposium on Networked Systems
Design and Implementation (May 2006).
- [37]
- Tati, K., and Voelker, G. M.
On object maintenance in peer-to-peer systems. In Proc. of the
5th International Workshop on Peer-to-Peer Systems (Feb.
2006).
- [38]
- van Renesse, R., and Schneider,
F. B. Chain replication for supporting high throughput
and availability. In Proc. of the 6th Symposium on Operating
Systems Design and Implementation (Dec. 2004).
- [39]
- Weatherspoon, H., Chun, B.-G., So,
C. W., and Kubiatowicz, J. Long-term data maintenance
in wide-area storage systems: A quantitative approach. Tech. Rep.
UCB//CSD-05-1404, U. C. Berkeley, July 2005.
- [40]
- Weatherspoon, H., and Kubiatowicz,
J. D. Erasure coding vs. replication: A quantitative
comparison. In Proc. of the 1st International Workshop on
Peer-to-Peer Systems (Mar. 2002).
- This research was supported by the
National Science Foundation under Cooperative Agreement
No. ANI-0225660, https://project-iris.net/. Andreas
Haeberlen was supported in part by the Max Planck Society. Emil Sit
was supported in part by the Cambridge-MIT Institute. Hakim
Weatherspoon was supported by an Intel Foundation PhD
Fellowship.
|
