
To understand the problem, consider the following simple example code:
char id(char x) { return x; }
...
tainted char t;
untainted char u;
char a, b;
a = id(t); /* 1 */
b = id(u); /* 2 */
Because of call 1, we infer that x is a tainted
char, and therefore we also infer that a is
tainted. Then call 2 typechecks (because
While this is a sound inference, it is clearly overly conservative. Even though this simple example looks unrealistic, we encounter this problem in practice, most notably with library functions such as strcpy. This leads to a large number of false positives.
The problem arises because we are summarizing multiple stack frames for distinct calls to id with a single function type--x has to either be untainted everywhere or tainted everywhere. The solution to this problem is to introduce polymorphism, which is a form of context-sensitivity.
A function is said to be polymorphic if it has more than one
type. Notice that id behaves the same way no matter what
qualifier is on its argument x: it always returns exactly
x. Thus we can give id the signature
![]() for any qualifier
for any qualifier
![]() .
.
Operationally, when we call a polymorphic function, we
instantiate its type--we make a copy of its type, replacing
all the generic qualifier variables ![]() with fresh qualifier
variables. Intuitively, this corresponds exactly to inlining the
function, except that instead of making a fresh copy of the function's
code, we make a fresh copy of the function's type.
with fresh qualifier
variables. Intuitively, this corresponds exactly to inlining the
function, except that instead of making a fresh copy of the function's
code, we make a fresh copy of the function's type.
We need a way to write down polymorphic type signatures--for example, we should be able to express that if the strcat() function is passed a tainted second argument, then its first argument should also be tainted, but not vice versa. We can do this by writing a polymorphic type with side constraints on the qualifiers:

This theorem enables us to define the partial order implicitly by the
naming of the qualifier variables on the function arguments and return
type. We represent a qualifier ![]() in the partial order
in the partial order ![]() by
by
![]() , which we denote as a '_' separated string of the integers
in the set. If
, which we denote as a '_' separated string of the integers
in the set. If
![]() , then
, then ![]() is represented as
is represented as
![]() . Hence, the polymorphic declaration of strcat can
now be written as
. Hence, the polymorphic declaration of strcat can
now be written as
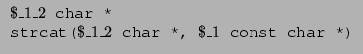
To keep our implementation simple, we only support polymorphism for library functions, i.e., functions with no code. To be more precise, any function may be declared polymorphically, but the polymorphic prototype will not be typechecked against its implementation. This restriction is not fundamental; there are well-known efficient algorithms for more general polymorphism [19,33]. Our standard prelude files contain appropriate polymorphic declarations for most of the standard library functions.