|
USENIX Technical Program - Paper - Smartcard 99
[Technical Program]


Next: Acknowledgements
Providing authentication to messages signed with
a smart card in hostile environments
Tage Stabell-Kulø, Ronny Arild, and Per Harald Myrvang
Department of Computer Science
University of Tromsø
Tromsø, Norway
{tage,ronnya,perm}@pasta.cs.uit.no
Date: 24. March 1999
Abstract:
This paper presents a solution to how a smart card can be used to
sign data in a hostile environment.
In particular, how to use a smart card to make a signature on
data when the machine to which the smart-card reader is attached can
not be trusted.
The problem is solved by means of a verification server
together with a substitution table and a one-time pad; it is argued
that lacking a trusted channel from the card, our solution is
minimal.
An invalid signature (a signature on data not intended to be signed)
can only be made if the online server colludes
with the machine the user is using.
In all other circumstances, only a denial-of-service attack is
possible.
The realization is applicable in practice, but slightly awkward.
It is difficult to digitally sign data in a hostile environment, even
armed with a smart card that can create digital signatures by means of
some public-key
technology [3].
Assume a user P sitting in front of a machine M with the smart
card residing in a smart-card reader connected to M.
If P wants to sign X, he has no means to verify that M actually
gives X to his card;
thus, P can not use the card without trusting M just as much
as he trusts the integrity of the card, in which case he could use Mto sign rather than involving a smart card in the first place.
The problem is that there is no authenticated ``channel'' from the
card to the user.
The card is unable to ``tell'' P what it is about
to sign, and P can not verify that X has been received for
signing [1].
The problem is well known [4,14].
Authenticated channels can be obtained by means of, for example, more
powerful hardware, such as contemporary PDAs.
With this type of hardware, integrity is obtained since the PDAs have
a (small) display on which X can be shown.
However, smart cards are prevalent and we seek a solution using this
technology.
In general, data integrity relies on either secret information or
authentic channels [7].
In other words, when using smart cards without any authentic channels,
some sort of secret information is needed.
There are many settings where one might desire to sign data with a
smart card, where the environment might be hostile.
For example a point-of-sale terminal, or during a visit to an
``Internet café''.
Using a computer laboratory at a university is another example.
In general, any environment where one does not want to include M in
the trusted computing base (TCB), for whatever reason [13].
The paper is outlined as follows.
Section 2 is concerned with describing the system and
our solution.
Then, in Section 3, our protocols are shown and
analyzed.
Section 4 discusses related work.
In Section 5 we present conclusions and give directions
for future work.
Overview
This paper examines a particular--albeit common--setting where
smart cards are
employed.
The general idea is that the user P has some data, an email perhaps,
that he wants to sign, using the secret key stored in his card.
He would instruct the software running on M to send the data to the
smart-card reader, insert his card, and having the signature returned
in order to be attached to the email.
The problem is that M might give any data to the card, and the card
will sign.
Unless P can verify public-key signature in his head, he has no
means to judge whether M is trustworthy or not.
In fact, what seems to be a single problem really poses three distinct
challenges:
- 1.
- How can P ensure that the correct data has
been signed?
- 2.
- How can P verify that the signature is valid?
- 3.
- Is it possible for a third party to conclude
that P has verified that the correct data has been signed?
The last is required if the signature P makes with his card is
to have a non-trivial value.
Concerning the first question, only P knows the answer to this, since only
he knows what he intended to have signed; the fact that M also happens
to know is of no relevance to us because M is not trusted.
The user must thus be involved in providing an answer to the first
question.
Or, in other words, no solution to this problem can be envisioned
without involving the user in some way, after the signature has been
made.
In a realistic scenario, we can rule out the possibility of Pverifying the signature himself.
This implies that a third party must verify the signature itself.
Such a third party should take the form of an online service, in order
to better enable the user to timely obtain an answer the second question.
This, however, raises a new obstacle: How can this online service,
called O, communicate with P over a channel that provides
integrity?
Our contribution is a working method to solve this particular
problem.
Turning now to the third challenge, it will become evident that Pcan sign a certificate that, together with the credentials our
solution creates as it progresses, enables others to conclude that the
data indeed was signed by P's card, with P's consent.
It might be worth noting that we are only interested in signing.
P is unable to encrypt anything on his smart card without trusting
M.
That is, secrecy can not be obtained at all in the setting we
describe.
Our solution consists of three parts, an on-line service, a small
one-time pad (an OTP) and a shared secret.
In the following we will describe how some data is signed by means of
a smart card in a hostile environment (details are given in
Section 3).
We use the notation from the BAN logic [2],
- 1.
- The machine M is not trusted.
Thus, M is not the logical sender or recipient of any message (even
though the actual hardware will be used to send messages).
From a logical point of view, M is part of the communication
infrastructure.
In this light, the only principals of interest are the user P, his smart
card C and the on-line service O (to be described below).
- 2.
- The user has some data X, which typically is a string of
characters (i.e., a text).
P inserts his card (into the smart-card reader attached to M)
and instructs M to transfer the data to the card.
The card is then instructed to sign the data it received.
- 3.
- The card accepts the message and signs X, creating
XKC-1.
Notice that C has no means to verify that X actually originates
from P.
As mentioned above, two questions must be answered:
- (a)
- Is the signature valid?
- (b)
- Has the correct data been signed?
The online service can be used to verify the signature's validity; the
signed data is sent to O.
- 4.
- The crux of our solution is that O can send back to P a
transformation f of the data it has verified.
Assume that P and O share a small secret one-time
pad and a secret number.
After verifying the signature on X, O will create
two new message as follows.
Using the one-time pad, a new message Z = f(X) is constructed, and
sent to P.
Z is thus the message X transformed for integrity under a
one-time pad.
We will discuss this transformation below.
If the signature is valid, O constructs a certificate
asserting this fact.
The certificate is sent to a public server of some sort.
We call this server S, its existence is only for convenience
and might very well be O itself.
A random number Y is associated with each one-time pad.
Y is known only to P, but H(Y) is known also by O.
If O finds that the signature is valid, O will sign a
certificate stating this fact; the certificate will include
H(Y).
By releasing Y, P proves that he accepts the signature.
- 5.
- When Z is received by P, he can without much effort (and
without using M to anything but display Z) verify that
Z=f(X).
Since Z is a transformation of X, P can conclude that the
content was what he intended to sign, and that his trusted server
O has verified the signature.
P now releases Y by sending it to S.
To sum up, O verifies the signature made by C, and Packnowledges the actual text by releasing Y.
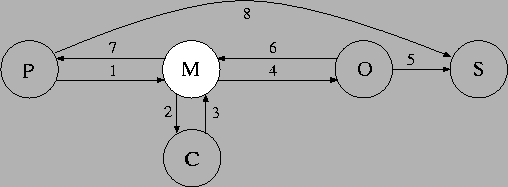
Figure 1:
The protocol run
 |
Up to this point we have used logical messages.
If we look at the actual implementation we find eight messages being
sent over various channels; see Figure 1.
The messages can be described as follows:
Messages 6 and 7 contains the string of digits O has constructed
based on its copy of the OTP.
Since the OTP is secret, the string is X combined with a secret.
In BAN such a construction is denoted as
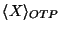 . .
Section 3 gives a detailed description of the small
one-time pad that is required, a closer look at the messages that
are sent and, most important, a careful analysis of the logical meaning
of each message and of the certificates that are required to conclude
that X was signed by C with the consent of P.
Signing
This section starts out by presenting the details of the one-time
pad.
Being small it is suited for practical use; Section 3.1
discusses it.
Section 3.2 is concerned with a theoretical analysis
of the certificates and credentials required to assert that a signed
statement from a smart card logically originates from the user that
control the card.
In Section 3.3 we discuss the trusted computing base of our
solution.
Section 3.4 describes the implementation status, and
gives a preliminary performance analysis.
The one-time pad
We assume that P does not have any significant computational resources at
hand (M can not be trusted).
Since it is unreasonable to assume that any user can verify digital
signatures without the help of a computer, we must thus construct a
secure channel from O to P, on which a message can be sent.
That is, P needs to receive from O some information that convinces
him that the correct text was signed.
This information must be a function of the message X in order for
P to know that the correct text has been signed.
In addition, P must be convinced that the message he receives
comes from O.
Taken together, the channel we are about to construct must provide
authentication
(since authentication implies integrity [7]).
Clear-text attacks are indeed a threat since M knows X.
If, on the other hand, X was unknown to M then P and O could
share a list L of random numbers,
each number Li of L being
as long as X.
O would verify the signature on X, calculate
Z = X + Li and
send the result to P.
P would be able to calculate Z - Li and verify that the card
had signed X.
This cipher would be perfectly secure [9].
In our system, each OTP contains two small tables.
The first contains random numbers, as one would use to create a
one-time pad.
However, in our case X is known, and this procedure alone offers no
integrity at all.
This is so because if 'A' and a random number yields 12 then 'B' must
have yielded 13.
We overcome this problem by incorporating an additional table.
It is a permutation of the characters;
we denote this a substitution table.
We now describe the OTP used by P and O.
In the current implementation, the alphabet available to P are all
the upper-case characters, space (denoted as ` '), dot
(`.'), the digits and the two symbols $ and @; 40 characters in all.
These characters are matched with a table of random numbers, assigning
a random number to each character.
Appendix 1 shows two examples of tables; each has six rows:
- Letter:
- The alphabet available to users
- Subst:
- The substitution table; each character from the
alphabet is replaced by the corresponding number from the
substitution table.
- X:
- In this row the user writes his message
- OTP:
- The number representing each character is added (modulo
40) to the corresponding element in the One Time Pad.
- Z:
- The result.
- Y:
- A secret number, see below.
When P receives Z from O, he would want to verify the result.
In order to do so, he proceeds as follows.
- 1.
- Count the number of characters in the message,
and prepend this number (as a string) to the message.
- 2.
- Write the string in the table (in the row marked X) above the
random numbers.
- 3.
- For each character, add the ordinality of the character (taken
from the substitution table) with the random number.
The addition must be done modulo 40 (the number of characters).
An example of a table which is filled in is shown in the Appendix.
The string ``GIVE TAGE@ACM.ORG $500.'' is encrypted for authentication.
If P sees that Z indeed is the correct transformation of X, he
will release Y.
The certificate generated by O contains H(Y), but Y is only
known to P.
In other words, by releasing Y, P makes it known that he supports
the certificate issued by O.
Theory
The security of our system hinges on three properties.
The first is that one component in each sum is a random number.
Randomness ensures the resulting list of numbers are random.
No amount of calculation or number of previous messages can give
information necessary to alter the text.
Second, each OTP and substitution table can only be used once.
Third, text can not be appended to the string.
Obviously, the length of the string that can be transmitted (and
verified) in this manner is restricted by the length of the pad.
However, the pad can be made as long as one desires and the amount of
work to verify a message increases linearly with length.
Another way to increase the task of verification is to increase the
alphabet length (now being 40).
If this length is increased, the OTPs and corresponding substitution
tables must be increased accordingly.
We have described how a user P can sign a message; we now describe
how a receiver verifies that a signed message is valid.
Assume a user Q receives a message
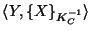 from P.
Assume furthermore that Q believes that C belongs to P.
Upon receiving the message, Q contacts S and asks for the
certificate that O should have generated.
Obtaining it, Q has all he needs to conclude that X was signed by
C, that O has verified that the signature was in order, and that
P has verified that the correct data was signed.
from P.
Assume furthermore that Q believes that C belongs to P.
Upon receiving the message, Q contacts S and asks for the
certificate that O should have generated.
Obtaining it, Q has all he needs to conclude that X was signed by
C, that O has verified that the signature was in order, and that
P has verified that the correct data was signed.
Table 1: Messages and their interpretation
Message |
Meaning |
| X |
X |
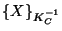 |
C says X |
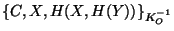 |
O|C says X,
O|Y says X |
| Y |
Y |
|
The four datums that are available to Q is shown in the left column
of Table 1.
Informally, the fact that P has released Y is proof that P has
verified the signature.
We will now give a more formal view of the system, using the theory
from [6].
If Q is to act upon X he would need a certificate, signed by P(or a principal Q believes speaks for P), asserting that
possessing the four items together vouches for the conclusion that Xoriginates from P.
Since M is not trusted, P does not control C, and the assumption
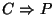 is unwarranted.
The intention of P is that no-one will hold him responsible for any
message X unless the following conditions are met:
is unwarranted.
The intention of P is that no-one will hold him responsible for any
message X unless the following conditions are met:
- X is signed by C.
- The signature made by C is verified by O.
O must say that C have said X.
- O must tie (the secret) Y to the signed message.
This enables P to accept the signature by releasing Y.
- Y is available.
All this is captured in the following certificate
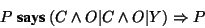 |
(1) |
Since Y is secret, Q is unable to satisfy the certificate
(1) unless P releases Y.
In practice, S could in addition act as an on-line verification for
the validity of C in that P would make C issue
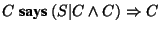 ,
see [6]
for details. ,
see [6]
for details.
With these credentials, the axioms and interference rules set forth
in [6], it follows that
P says X.
Note that the use of Y give the message the properties of a
transaction authentication as defined in [7];
message authentication and the use of time-variant parameters
(timeliness or uniqueness).
Trusted Computing Base
As can be seen from (1) it is a prerequisite for
certificate verification that O says that Y says X.
However, P does not want to include O in his TCB.
O has not been given Y by P, but rather H(Y).
When O quotes Y as saying X it might turn out that O is
mistaken; this is in fact correct, in the cases where M, for
example, mounts some attack.
In other words, when Q collects credentials he might or might not be
able to locate Y.
In such a situation there are two possibilities: Either P has not
released it (he has detected an attack) or Y has been delayed or
deleted as part of a traditional denial-of-service attack.
Since P is at the mercy of M, there are no means to defend Pagainst denial of service.
O is a trusted third party in that P trusts O to act
according to the protocol (not to certify that a signature is good if
it is not).
On the other hand, O is not able to deceive P without colluding
with M.
When O and M colludes, M can feed a false message to the card
and let O send an erroneous message back to P.
The important issue is that alone, O can not conceive P.
In the same manner as O is not in the TCB, neither is S, nor C.
No principal is in a situation to make P release Y, which will
erroneously make (1) is true, without colluding with some
other principal.
Performance
The system described is not yet fully implemented, although the
infrastructure is; this includes a verification server, certificate
and signature handling, and a cryptographic strong random number
generator. We have, however, done preliminary performance tests using
predefined OTPs and substitution tables.
Experiments show that verification is initially done at a speed of
approximately 7-8 seconds per character.
However, speed increases as one gets accustomed to the calculation.
Experienced users spend approximately 3-4 seconds per character.
Slightly slower than typing, but in our opinion worthwhile.
Related work
Our solution is basically a Message Authentication Code (MAC).
MACs are well covered in the literature,
see for example [10,7,11].
However, most MACs are computationally intensive.
Most types of MACs, such as MD5 [8], are surjective, and
require some computation to be secure (mapping one language onto a
smaller while being a one-way function).
The use of unconditionally secure MACs are described in [11, Chapter
10] with the use of orthogonal arrays (OAs).
These OAs seems, however, to be infeasible to work with for human
beings compared to substitution tables and OTPs that only require the
use of elementary arithmetics.
Authentication by means of a secret one-time pad is an old
invention [5].
In this article, we have combined the one-time pad with the release of
a secret to authenticate that the verification of the signature.
Conclusion
We have shown that users can achieve secure authentication to messages
signed with a smart card in hostile environments, using a partial
trusted verification server together with a substitution table and a
one-time pad.
The applicability lies in that short messages with small character
sets.
We are working on implementing the system described in this paper,
using Cyberflex Open16K smart cards1 that run a Java VM, based on the Java Card 2.0
specification [12].
Since these cards come without a coprocessor (for efficiently doing
computations on large integers), signatures made with
public key schemes such as RSA or ElGamal would be hard to implement
efficiently.
We are looking into this issue.
In addition, we are also working on eliminating O from the protocol
by storing OTPs and substitution tables on the smart card itself (this
would require about 100-150 bytes of storage capacity for each
OTP/substitution set).
Making the verification process easier for end-users is also
prioritized; using arrow keys to decrypt the message from O may be a
workable solution.
This is not a new idea; the use of arrow keys for decrypting OTPs was
suggested in [14] and was based on the insertion of `+' and
`nextdigit' operations described in [1].
A way to eliminate the awkwardness of using OTPs and substitution
tables would be to insert a channel between O and P for Message 6
in the protocol run.
A mobile telephone could be used for this purpose, where O sends Xand Y to P through, for example, the GSM network.
P would then see that the message received on the phone's display
corresponds with the message that was originally written by P.
A drawback here is that P and O must share the secret Y, since
M could otherwise send X to P (through GSM).
This implies that P must trust that O does not release Y until
P does it.
This drawback, combined with that O can no longer be eliminated from
the protocol, would probably not detract from the fact that P no
longer needs to do substitutions and arithmetics in his head (or use
arrow keys).
Footnotes
- ... cards1
- Information about these
smart cards is available at URL:http://www.cyberflex.slb.com/.


Next: Acknowledgements
Per Harald Myrvang
1999-03-23
|
