
2007 USENIX Annual Technical Conference
Pp. 309–322 of the Proceedings
A Comparison of Structured and Unstructured P2P Approaches to Heterogeneous
Random Peer Selection
*
Vivek Vishnumurthy and Paul Francis
Department of Computer Science, Cornell University, Ithaca,
NY 14853
{vivi,francis}@cs.cornell.edu
|
Abstract:
Random peer selection is used by numerous P2P applications; examples include
application-level multicast, unstructured file sharing, and network location
mapping. In most of these applications, support for a heterogeneous capacity
distribution among nodes is desirable: in other words, nodes with higher
capacity should be selected proportionally more often.
Random peer selection can be performed over both structured and unstructured
graphs. This paper compares these two basic approaches using
a candidate example from each approach. For unstructured heterogeneous
random peer selection, we use Swaplinks, from our previous work.
For the structured
approach, we use the Bamboo DHT adapted to heterogeneous selection using our
extensions to the item-balancing technique by Karger and Ruhl. Testing the
two approaches over graphs of 1000 nodes and a range of network churn
levels and heterogeneity distributions, we show that Swaplinks is the superior
random selection approach:
(i) Swaplinks enables more accurate random selection than does the structured
approach in the presence of churn, and
(ii) The structured approach is sensitive to a number of hard-to-set tuning
knobs that affect performance, whereas Swaplinks is essentially free of such
knobs.
1 Introduction
A number of P2P or overlay applications need to select random peers from the P2P
network as part of their operation.
A simple but poorly scaling way to do random peer selection is to
disseminate a list of all nodes to all nodes. To randomly select
another node, each node simply selects randomly from its list.
Early gossip protocols that needed uniform random peer selection typically
assumed this approach. A scalable alternative approach is to build a sparse graph
among the peers, and then use some kind of walk through the graph
to do random node selection.
An early example of this approach was an overlay
multicast protocol called Yoid [1]. Yoid constructed a random graph
over which random walks would be used to discover nodes that
might be included in a multicast tree.
More recent overlay multicast protocols that utilize random
node selection include Bullet [2] and Chainsaw [3].
Gnutella-style unstructured file sharing networks utilize a random selection
component when searching for nodes having desired files. To improve the
scalability of this file search, GIA [4] proposes using random walks
rather than flooding.
Random node selection also plays an important role in proximity addressing schemes like Vivaldi [5] and
PALM [6]: these schemes need to select random peers in the network to measure their
latencies from the peers and compute their coordinates.
In many of these examples, it is important that random selection
follow a given non-uniform probability distribution. In other words,
some nodes are to be selected with higher probability than others. The
primary reason for this is to accommodate nodes with differing
capacities. We refer to this problem of selecting each node with probability
proportional to its specified capacity as heterogeneous random selection.
The need to accommodate heterogeneity is especially acute for file searching in Gnutella-like file sharing networks, as the use of super-nodes attests.
The primary focus of GIA is this heterogeneity in unstructured networks.
Accommodating node heterogeneity is also important in overlay
multicast algorithms [7, 8, 9, 10].
Given the number and variety of P2P and overlay
applications that use random node selection,
in previous work [11], the authors designed
Swaplinks, a general-purpose unstructured P2P algorithm to provide a
heterogeneous random node selection primitive that could be used
by a wide range of P2P and overlay applications.
Swaplinks builds a random graph in which each
node's degree is proportional
to its desired degree of heterogeneity, and then uses random walks
over that graph to do node selection.
The previous work showed, using simulations, that Swaplinks was the most
attractive unstructured random selection technique:
It gives fine-grained control over
both the probability that a node is selected and
the overhead seen at each node.
It is efficient, scalable, robust (to churn, and to wide variations in node
capacities), and simple.
In this paper, we implement Swaplinks, and provide a comprehensive evaluation of
the Swaplinks implementation, thus validating the previous simulation results.
Heterogeneous random selection in the example applications cited earlier can
also be potentially realized by structured approaches. Our previous work,
however, examined only unstructured approaches to random selection, because of
our intuition that they would be simpler than structured approaches, and that
this simplicity would ultimately lead to a more scalable and robust system.
A primary goal of this paper is to test our intuition about the relative
simplicity of structured and unstructured approaches to heterogeneous random
selection through a performance comparison between the two
approaches.
We choose the “item-balancing” algorithm by Karger and Ruhl for
load balancing in structured P2P networks [12] as the basis for
the structured random selection approach, and we use Swaplinks as the
unstructured approach.
The basic idea in using the item-balancing algorithm in our setting is to assign
identifiers in the DHT number space such that a larger portion of the number
space maps proportionally into high-capacity nodes, and a smaller portion maps
into low-capacity nodes. High capacity nodes, by virtue of “owning” a
larger portion of the number space, will be selected proportionally more
often by queries issued to uniformly random identifiers.
We implement the Karger/Ruhl approach over the Bamboo DHT [13], and
call this approach KRB.
We chose Bamboo because it is a stable well-maintained open software for DHTs,
and because it is a second generation DHT, designed using the best principles
from the earlier, first generation DHTs (like Chord [14] and
Pastry [15]).
This minimizes the chances that the results are an artifact of
a poor DHT implementation.
The performance comparison between KRB and Swaplinks shows that KRB performs less well in the face of
churn, and has a number of hard-to-set tuning knobs that affect performance.
While we need more comparisons (with other structured approaches) to be certain of
this, the performance comparison goes a long way toward
validating our intuitive concern about the relative complexity
of using DHTs for heterogeneous peer selection.
Overall, this paper makes two contributions:
-
We implement an open source library [16] that provides
heterogeneous unstructured random graph construction and
random node selection primitives based on Swaplinks.
We also measure the performance of the Swaplinks implementation for both
random graph construction and random selection,
and in so doing validate earlier simulation results.
- We modify the Karger/Ruhl load balancing
algorithm for heterogeneous random peer selection,
and compare its performance as a random selection mechanism with that of
Swaplinks.
We next describe related work in Section 2.
We describe the Swaplinks algorithm and its implementation in
Sections 3 and 4, and the KRB method in
Section 5. In Section 6 we give a performance evaluation
and comparison of both algorithms.
Finally, we discuss issues and future work in Section 7.
2 Related Work
2.1 Structured P2P Networks
All structured P2P systems modeled as DHTs (e.g. [17, 14, 15], etc.) assign identifiers to nodes, typically at random.
Random selection in DHTs can be done by randomly choosing
a value from the DHT number space, and routing to that value.
The problem of random node selection in DHTs, then, boils down to
the problem of assigning identifiers appropriately.
Even where uniform random selection is desired, assigning a single
random identifier to each node is inadequate, because any
non-uniformities in the random assignments persist over time.
Consistent hashing schemes deal with this by assigning multiple
random identifiers[18], and DHTs have proposed
something similar, namely creating multiple virtual replicas of
each node in the DHT.
To achieve heterogeneity, each node is replicated a number of times
proportional to its capacity ([19, 20]).
This approach however entails a blowup in network and computational
overheads, and so is not an attractive approach.
A modified multiple virtual node approach is used in Y0 [21]. Here, virtual node
identifiers for each node are
selected from a small range of identifiers;
the authors utilize the proximity of the
node's identifiers to avoid having to maintain separate routing entries for each
virtual node.
While this scheme is interesting, and a potential candidate for comparison, it
has not been analyzed or tested for robustness to high churn.
Y0 also needs all nodes to know (at least roughly) the number of nodes in the
system, which might be an issue under high churn.
Ledlie and Seltzer [22] present the k-choices algorithm for
load balancing in settings with skewed query distributions and
heterogeneous capacities. k-choices is similar to
KRB, in that both place nodes at IDs that minimize load imbalance.
The difference is that
k-choices assumes that each node knows its absolute desired load,
whereas in KRB, nodes only have a notion of relative desired load.
Accordion [23] and HeteroPastry [24] give
schemes that tailor nodes' degrees and their message loads according to
capacity and network activity. These schemes however do not provide
capacity dependent namespace partitioning, and so cannot support heterogeneous
random selection by routing to uniformly randomly selected IDs.
An alternative approach might have been to use unbiased random walks over
these networks for random selection, but
the control over degrees in these schemes is not fine-grained enough (i.e.,
average node degrees are not proportional to capacities) for this
to result in the desired selection distribution1.
Karger and Ruhl propose two schemes in their papers for load balancing
in DHTs [12, 25].
The first results in a constant factor bound on ID spaces between successive
nodes, but cannot handle the case where the ID spaces are to be split
according to capacities.
The second scheme looks at item load balancing, where the number of items that
are stored at any node should be within bounds and dependent on node capacity.
With minor variations, we could modify this scheme to split ID space according
to node capacities and run over Bamboo – we call this KRB.
We use KRB as the candidate structured approach for our performance comparisons.
2.2 Unstructured P2P Networks
In previous work [11], we found Swaplinks to be the
best algorithm for constructing unstructured P2P graphs suitable for
heterogeneous random selection. Here is a brief overview of other unstructured
approaches.
GIA extends Gnutella by making both graph-construction and query-resolution
sensitive to node capacities [4]. High-capacity nodes here have higher
degrees, and are more likely to be traversed by random walks.
While Swaplinks shares these two features with GIA,
Swaplinks exhibits more accurate control over degree and probability of
selection.
Other examples of unstructured graph construction schemes include Araneola [26], an
approach by Law and Siu [27], and SCAMP [28]. None of these
take node heterogeneity into account.
The Ransub [29] mechanism can be used as a random node selection
primitive, but as was the case with the previously mentioned schemes, does not
take into account node heterogeneity.
The Metropolis-Hastings algorithm [30] and the
Iterative-Scaling algorithm [31] can be
used to achieve desired probabilities of selection over any underlying graph.
But when the underlying graph has node degrees close to the desired
probabilities, like Swaplinks does, random selection primitives achieve the
desired distribution much more efficiently (e.g., random walks need to take far
fewer hops).
3 The Swaplinks Algorithm
Our random selection API consists of the following core procedures:
-
join(numLinks)
- node = select()
- listOfNodes = listNeighbors(callBack)
The join() procedure causes the joining node to establish random
links with other, already joined nodes.
The parameter numLinks indicates how many neighbors the joining
node should try to obtain.
On average a node will end up with twice as many neighbors as
the value numLinks.
This is because other nodes will in turn select a given node as
their neighbor.
The value of numLinks is set to be proportional to the probability
with which the node should be selected.
For instance, if a node A should be selected with twice the probability
of node B, then node A will set numLinks to be twice that
of node B.
It is up to the application to know what values to choose for numLinks.
Typically an application would choose a value of numLinks=3 for
its lowest capacity nodes, and select values proportionally higher for
higher capacity nodes.
The value 3 is chosen as the minimum to insure that even the lowest
capacity node has a low probability of partition from the rest of
the network.
Higher values reduce the probability even more.
When a node wishes to randomly select another node, it calls
select().
This causes a random walk to be taken through the random graph.
The number of hops in the walk is a fixed value, 10 by default.
The node at which the walk ends is the selected node.
The value numLinks plays two important roles here.
First and foremost, the Swaplinks design ensures that the walk will end at
nodes with higher numLinks values
with proportionally higher probability.
Second, nodes with a higher numLinks value will serve as intermediate
hops in walks with higher probability.
This second effect results in the load required to participate in
the algorithm by any given node to also be proportional to its capacity.
There are a number of possible variations on the select() call:
for instance
the length of the walk may be specified, or the
identity of all nodes traversed during the walk may be returned.
Some P2P applications may simply wish to use the underlying graph directly.
For instance, a BitTorrent might use the neighbors selected by the
join() procedure as the nodes with which it exchanges file blocks.
The listNeighbors(callBack) procedure allows this.
In addition to providing the current set of neighbors, a callback
routine allows Swaplinks to inform the application whenever the
neighbor set has changed.
In building and maintaining a random graph, each node labels each
of its links to a neighbor node as either an outlink or an inlink.
These labels have nothing to do with the direction messages may pass
over them: messages may pass in both directions.
Rather, the label is chosen based on which node initiated creation
of the link.
The node that initiated the link labels it an outlink, and other node
labels it an inlink.
Correspondingly, neighbor nodes are labeled as out-neighbors or in-neighbors.
The outdegree is the number of outlinks, and the indegree is
the number of inlinks.
Every link is an outlink in one direction and an inlink in the other.
Likewise, there are two types of fixed-length random walks:
OnlyInLinks: The walk is forwarded to a randomly chosen in-neighbor.
OnlyOutLinks: The walk is forwarded to a randomly chosen out-neighbor.
Every node always maintains an outdegree of numLinks, by finding numLinks
out-neighbors when it first joins, and by replacing any out-neighbor it loses
with another one.
This is done in such a way that nodes tend to have the same number of inlinks
as outlinks, though they may have slightly greater or
fewer than numLinks inlinks.
There are three cases the algorithm must cover:
-
A joining node is adding selected out-neighbors
- A node is replacing a lost out-neighbor
- A node is replacing a lost in-neighbor
To find a new out-neighbor for the first case, a
joining node (say A) initiates a fixed
length OnlyInLinks walk from one of its entry nodes.
The node (say B) where the walk
ends is chosen as an out-neighbor for the new node.
Node B then randomly selects one of its in-neighbors C,
and “gives” that in-neighbor to A. In other words,
C loses B as an out-neighbor, and gains A as an
out-neighbor.
The result of this transaction is that A gains both an
out-neighbor (B) and an in-neighbor (C). After A is
done finding all of its numLinks out-neighbors, it will
also have an equivalent number of in-neighbors.
Node B will have gained one in-neighbor (A) and lost
another (C), so it comes out even.
Node C will have lost one out-neighbor (B) and gained
another (A), so it also comes out even.
If a node (say A) loses an existing out-neighbor (the
second case above), it likewise takes an OnlyInLinks walk,
and creates an outlink with the discovered node (say B).
However, in this case, B does not give one of its
in-neighbors to A. Rather, B ends up with an extra
in-neighbor. Had B given A an in-neighbor, then A would
have ended up with an extra in-neighbor instead.
Finally, if a node (A) loses an existing in-neighbor (the third
case above), it sees if its number of in-links is less than its numLinks. If
so, it takes an OnlyOutLinks walk. The node (B) discovered by the walk then
donates one of its in-neighbors to A if B's number of inlinks is greater
than half its numLinks.
The above modes of link-formation could lead to the creation of multiple links
between the same pair of neighbors; Swaplinks makes no effort to eliminate these
multiple links. This makes dealing with very small networks straightforward.
The rationale behind using the OnlyInLinks and OnlyOutLinks walks in Swaplinks
is as follows: The OnlyInLinks walk selects each node with a probability
roughly proportional to its outdegree. The OnlyOutLinks walk, on the other
hand, selects each node with probability roughly proportional to its indegree.
Thus Swaplinks, by using the OnlyInLinks walk, ensures that the load placed on
each node is proportional to its outdegree. And by employing OnlyOutLinks to
deliberately look for inlinks in the presence of churn, it tends to find nodes
with disproportionately large indegrees, thus stealing the surplus inlinks
from such nodes and ensuring that nodes' indegrees stay close to their
outdegrees.
In this paper, application-requested node selection (select()) uses
OnlyInLinks walks, as opposed to the other random walks tested in
[11]. While both OnlyInLinks and the random
selection walks in [11] result in selection
proportional to nodes' outdegrees, OnlyInLinks is simpler and thus the more attractive method to use.
Simulations in [11] show that Swaplinks
builds graphs where the degree distribution closely resembles the
desired distribution. The graphs scale well to large sizes,
and lend themselves well to random peer selection.
The resultant message load on nodes and
the frequency of selection vary linearly with the degree.
Swaplinks implementation results presented later in this paper corroborate these
findings.
A feature of Swaplinks that makes it attractive from a practical viewpoint is
that it is free of “tuning knobs”:
It has no parameters to set, apart from the neighbor heart-beat frequency
parameter (present in most distributed systems). We avoid having to tune the
hop-length for different random walks by making all walks 10 hops in length,
which is a conservatively large value.
4 Swaplinks Implementation
Our system is implemented in C++ on Linux. We use TCP sockets for neighbor
connections. Each node sends heart-beat messages to each of its neighbors
every 2 seconds, and
assumes that a neighbor is dead if it does not receive a heart-beat from it
for 10 seconds. 2
A newly entering node initiates the required number of neighbor discovery
walks, restricting the number of outstanding neighbor walks to 10 at any
time.
A neighbor discovery walk is re-attempted if it fails
to return an appropriate neighbor within a period of 2 seconds.
We currently have an implementation of a rendezvous server that helps new nodes
join the system. The rendezvous server remembers a small number (currently 10)
of the most recently joined nodes, and newly joining nodes use these
nodes to
start their neighbor discovery walks. This rendezvous mechanism is
light-weight, and makes sure no single node is overloaded with the
responsibility of helping new nodes join the network.
The rendezvous mechanism could be made more robust by also having
the rendezvous server remember a small number of random other nodes in the
network, by periodically taking random walks, or by having newly joined nodes
report one or two of their neighbors.
The application using Swaplinks communicates with the Swaplinks module via a TCP socket.
Swaplinks exports the API described in section 3 to the
application over the socket by using appropriate serialization.
One application has currently been implemented over Swaplinks, namely
a heterogeneous overlay multicast protocol called
ChunkySpread [7] that
uses Swaplinks to both construct a heterogeneous random graph and
do random peer selection.
Each Chunkyspread node is involved in multicast data transmission (and
reception) with multiple other nodes; this set of peers is
a subset of the set of the neighbors in the Swaplinks graph.
A small set of ChunkySpread nodes (the nodes that originate the
multicast stream) need to discover an additional set of peers.
This is done using Swaplinks peer selection. In addition to ChunkySpread,
the Swaplinks algorithm is being used in other applications under
current development, like the NUTSS toolkit for NAT
traversal in P2P systems [32], and a P2P file backup system.
We are also currently experimenting with an alternate heart-beat mechanism,
called smart-pinging, that reduces heart-beat load at nodes with very
high degrees. We describe smart-pinging and give a preliminary evaluation of the
technique in Section 6.4.
5 Adapting Bamboo to Heterogeneity
Performing random selection on a DHT, with no regards to heterogeneity, and
assuming the ID space is apportioned uniformly among all nodes, is
simple: pick a uniformly random ID in the ID space, issue a random selection
query to that ID, and select the node where the query ends.
For this simple querying mechanism to still be applicable when there are
differences in node capacities, we need to split nodes' ID spaces
in proportion to their capacities (where a “node's ID-space” denotes the
extent of ID-space that the node owns).
For a simpler design of the heterogeneous random selection
scheme, we choose to compute a node's ID space as the space between its
successor in the ring and itself. We discuss how we simulate this feature in
Bamboo later in this section.
To achieve capacity-dependent ID space allocation, we develop a scheme
based on the item-balancing algorithm (henceforth referred to as K-R)
presented in [12, 25].
Nodes in K-R periodically send messages to one another, and share
loads when a load imbalance is perceived.
The item-balancing algorithm in [12] performs load sharing
through movement of nodes to new IDs, but does not address the issue of
heterogeneity, whereas the one in [25] takes heterogeneity into
account, but does load sharing by transferring
items from heavily loaded nodes to lightly loaded ones. Our scenario is
slightly different from either of the above two, since we need nodes to move
to new IDs so as to do ID space partitioning, and we need this partitioning
to be capacity sensitive.
We now outline KRB, our adaptation of the K-R algorithm.
The basic aim of KRB is to even out the relative loads of all nodes,
where a node's relative load is its ID space load divided by its
capacity.
As in K-R, each node periodically sends out a message to a
randomly chosen ID, embedding its load information – we call such messages
“KRB load messages”.
Noting that a node's moving to a new ID can affect the ID spaces of (up to) 3
nodes (the moving node, the moving node's old predecessor, and the moving
node's new predecessor), in KRB, we examine the change in load
at all nodes whose loads are
affected by the move. This is an extension of K-R, where the loads at only the
moving node and the moving node's new predecessor are examined.
If we examined the loads at only these two nodes, it would be possible for a
huge load to be inadvertently dumped on the unconsidered third node (the moving
node's old predecessor) as a result of the move; by considering all the three
nodes, we avoid this possibility.
Looking at a single KRB load message,
let us denote by S the node that
sent out the message, by R the node that receives the message,
and by P the predecessor of R. Now R decides if it should move to share
S's ID-space, based on the value of
the objective function, computed as follows:
|
r = | | LR + LS + LP |
|
| CR + CS + CP |
|
|
|
| |
ObjFn(R, S, P) = ΣN∈{R, S, P} | ⎪
⎪
⎪
⎪ | | ⎪
⎪
⎪
⎪ |
| | | (1) |
|
where LN is node N's ID-space load, which is equal to the space between N
and its successor, and CN is node N's capacity.
If R were to move, it would move to ID R' such that
That is, the new ID is the one that splits the space between S and its
successor in direct proportion to their capacities. If R were to move to
R', the objective function would take on a new value, computed similarly to
above. Finally, R does make the move if the objective function value reduces
by more than a threshold ratio (called the KRB-threshold, set to 0.2).
The computation of the objective function above can be seen as a greedy
step taken towards minimizing the system-wide objective function,
given below.
|
rall = | | ΣN in system(LN) |
|
| ΣN in system(CN) |
|
|
|
ObjFn(overall) = ΣN in system | ⎪
⎪
⎪
⎪ | | ⎪
⎪
⎪
⎪ |
(3) |
Since individual nodes do not know the value of rall, they use local
knowledge to compute r as shown above as an estimate.
The above description assumes that the node that sent the initial message S
is not already the predecessor of the node that receives the message R. If
R does happen to be the successor of S, there is no other third node whose
load will be affected if R were to move to any point in between S and its
successor. So now R moves if the following condition holds:
where we set є to 0.8.
This criterion is identical to the
one used in K-R.
Simulating a node's ID-space in Bamboo:
To make this scheme work in Bamboo, we need to make sure that the probability
that a node is selected is proportional to the ID space for which it is the
closest predecessor. However, in Bamboo, a query is routed to the node
numerically closest to the destination, rather than to the closest
predecessor.
So when a node receives a random selection query, it examines the intended
destination ID and forwards it to the immediate predecessor of that ID.
Our primary goal in adapting the Karger/Ruhl scheme to Bamboo was
capacity-sensitive random peer selection. Admittedly, this scheme does not
balance message load according to capacities (during the construction of the KRB
network or during random selection), as we only tailor nodes' ID spaces, and not
their routing tables. Accordingly, in this paper, we evaluate KRB as a
heterogeneous selection mechanism alone, and do not place emphasis on the message
load distribution that occurs while constructing the KRB P2P network.
Schemes that reactively tailor the neighborhood size based on capacity, such as
those proposed in Accordion [23] and
HeteroPastry [24] could be used with KRB to achieve both
capacity-sensitive probability of selection and capacity-sensitive message load
distribution during graph construction.
6 Performance Evaluation
We test Swaplinks through an emulation of a 1000 node network
on either a local (Cornell) cluster of 5 machines with 4 CPU's each, or a
20 CPU cluster on Emulab.
We achieve this size by launching a number of processes that in turn
launch the required number of individual instances of our system.
We preserve the semantics of communication here: all communication still takes
place through sockets.
The CPU loads here were mostly small enough to be negligible as a factor
in the results.
We also test the same implementation on PlanetLab.
For the emulation,
we use a Transit-stub [33] topology consisting of 100 routers to mimic
latencies between peers. Each peer picks a stub router uniformly at random.
All messages to be sent are buffered at the sender for the appropriate amount
of time (computed as a function of the stub routers of the source and
destination). We also add jitter
as a random value that ranges between 0 and 25%
of the end-to-end latency.
Launching KRB networks of a similar size (500-1000 nodes) by multiplexing
several instances on single hosts on local clusters
proved infeasible because of high CPU load factors due
to the Bamboo implementation. We instead evaluate KRB
using the simulator available with Bamboo's standard code distribution.
We use the same Transit-Stub topology as earlier to calculate message
delays in the KRB network.
We had to restrict our comparisons to 1000 node networks as the Bamboo
simulator, with our modifications, consumes too much memory for larger sizes.
All KRB nodes use a single entry node (called a gateway node by Bamboo) when they first enter the system.
A node that leaves its present spot and rejoins the system as part of the KRB
ID space readjustment scheme uses the set of neighbors it had before it left
the system as its gateway nodes.
We now give a road map of the experimental results that we will be presenting
in the subsequent portions of the paper. We first test 1000 node networks of
both Swaplinks and KRB under two different representative values of churn,
and, similarly under two different distributions of node capacities
(Section 6.1). Next, we subject both to more demanding churn scenarios: one where
network size doubles in the space of 10 seconds, and one where network size
halves instantaneously (Section 6.2). We give results of a 250-node experiment
over planetlab in Section 6.3.
Finally, in Section 6.4 we describe how we can use
“smart-pinging” to reduce the heart-beat load
incurred by high degree nodes.
In all of these experiments, we evaluate
Swaplinks as both a heterogeneous graph construction mechanism (e.g., how well
node degrees match desired degrees) and as a heterogeneous peer selection
mechanism (e.g. how close the selection probabilities are to the desired
values). We evaluate KRB on the other hand as solely a heterogeneous peer
selection mechanism.
6.1 Evaluation under representative churn scenarios
We use two separate churn scenarios: a “high-churn” scenario in which the median session time is 2
minutes , and a “low-churn” scenario in which the median session time is 30
minutes. These session time values have been taken from previous
studies [34, 35, 36].
We similarly use two capacity distributions: (i) The first capacity distribution is a `moderate' 5:10:20
distribution, with 80% of Swaplinks nodes having outdegree 5, 10%
having outdegree 10, and 10% with outdegree 20. We realize the same (relative)
capacity split in KRB by having 80% of the nodes have a capacity of
1, 10% have a capacity of 2, and 10% of the nodes have a capacity of
4.
(ii) The second capacity distribution is an `extreme' 3:60:150 distribution, with 98% of the nodes with outdegree
3, 1% of the nodes with outdegree 60, and 1% of the nodes with outdegree 150.
Again, we similarly realize the same relative capacity distribution in KRB as
well. We restrict the number of high-capacity nodes in the extreme capacity
distribution to the relatively small proportion of 1% for the following reason:
We run most of our experiments on networks of size 1000. With an increase in the
number of high-capacity nodes, it gets more likely that there is a
completely connected `core' made of the high-capacity nodes, and all
other nodes directly connected to the core nodes. The fact that this behavior is
not retained when the network grows to a larger size (where the network
maintains the
same capacity distribution) makes such networks not representative of general
P2P settings.
We use node session times that are independent of capacities, and follow the Pareto
distribution. Networks start from scratch (zero nodes),
and total experiment times are typically set to more than 5 times
the median node session times.
We ran tests where node session times were dependent on
capacities (i.e., where high capacity nodes are likely to stay in the system
longer) and where session times were Poisson distributed, and we found the
results to be similar to those we present here.
Unless otherwise mentioned,
we run ongoing background peer selections,
where the 80 longest living nodes perform a random selection every 250 ms for
the duration of their lifetime. We call such selections `periodic' selections.
We use the periodic selections to evaluate whether, for instance, the degree
20 nodes receive, in aggregate, twice as many selections as do degree 10
nodes, over the course of the experiment.
We also have two other nodes perform a `burst'
of 10,000 selections with a gap of 10 ms between successive selections.
We use the short-term
burst to obtain a set of selection measurements with relatively
little churn.
This allows us to more accurately compare the
measured distribution of selections among
a group of same-capacity nodes with the ideal distribution.
This is because each node present in the network during the burst
receives a statistically large number of (measured or ideal) selections.
The burst selections are performed just before the end of each experiment.
We measure message loads in both Swaplinks and KRB by counting only the
bytes in the message payloads; we do not consider TCP/IP or UDP header
overheads.
6.1.1 Swaplinks Results

| Figure 1: Swaplinks under high churn and moderate capacity distribution |
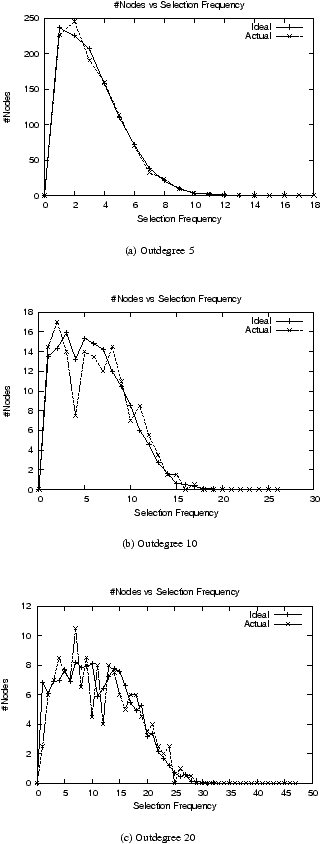
| Figure 2: Swaplinks #Nodes vs Selection Frequency for each degree:
high churn and moderate capacity distribution |
| | High Churn | Low Churn |
|
Target Outdeg | 5 | 10 | 20 | 3 | 60 | 150 | 5 | 10 | 20 | 3 | 60 | 150 |
|
Avg Load(B/s) | 150.26 | 297.87 | 581.49 | 98.16 | 1621.23 | 3449.41 | 124.33 | 247.34 | 491.49 | 79.62 | 1275.89 | 2903.17 |
|
Relative Load | 1 | 1.98 | 3.86 | 1 | 16.43 | 35.05 | 1 | 1.98 | 3.95 | 1 | 15.92 | 36.20 |
|
Avg Totaldeg | 9.68 | 19.41 | 38.23 | 5.80 | 111.77 | 255.25 | 9.98 | 19.93 | 39.95 | 5.98 | 119.98 | 298.18 |
|
Relative Selns | 1 | 2.01 | 3.95 | 1 | 19.78 | 44.43 | 1 | 2.00 | 3.99 | 1 | 20.10 | 50.16 |
|
Seln p-values | 0.815 | 0.862 | 0.977 | 0.757 | 0.579 | 0.819 | 0.292 | 0.784 | 0.583 | 0.224 | 0.957 | NaN |
|
| Table 1: Swaplinks results for moderate and extreme capacity distributions under high and low churn. |
Figures 1 and 2 show the results of
the high-churn, moderate capacity distribution experiment for Swaplinks.
The node degrees closely track the desired values,
while the selections and message loads are split among the different nodes in
proportion to their capacities: for example, nodes with outdegree 10 receive twice as many
selections, on an average, as the nodes with outdegree 5.
Both periodic and burst selections are counted to compute the curves in Figure
2.
Figure 2 shows the selection frequencies that result from
the burst selections. The figure has one plot for each of the three different
capacity classes, where a capacity class is just a set of nodes with the same
capacity. The “actual” curve represents the Swaplinks selections.
The “ideal” curve represents the ideal distribution of the particular class'
`fair share' of the total number of successful selections; the intersection of
each node's lifetime with the time-span of the burst selections is taken into
account in computing this distribution. These values don't include failed
selections, which occur with churn because nodes take about 10 seconds to detect
that a neighbor is down. Thus, the higher the churn-rate is, the greater the
probability is that a selection walk fails by being forwarded to a now-dead
neighbor at some hop. High churn has about 40%-45% failed selection walks,
while low churn has about 2% failed walks.
As can be seen from the plots in figure 2, Swaplinks' actual
selection frequency distribution closely tracks the ideal curve for each of the
different capacities. This, coupled with the fact that Swaplinks also realizes
capacity-wise selection distribution (Figure 1),
demonstrates that the selection mechanism realizes the desired
distribution.
Table 1 gives a summary of results from all of the
Swaplinks experiments in this section by averaging each value over the
second half of the experiment time. The duration of high-churn experiments here
is around 930 seconds, whereas the duration of the low-churn experiments is
around 14,000 seconds.
Each row in the table corresponding to a `relative' value
shows the corresponding value for the capacity class as a
ratio over the equivalent value in the lowest capacity class in the experiment.
Both periodic selections and burst selections are taken into account in
computing the `Relative-Selns' row.
The last row plots the χ2-
test p-values of the selection frequency distribution (for burst selections):
this is an indicator of how well the actual selection frequencies of nodes
within each capacity class match the ideal selection frequencies. Larger
values indicate a closer match; p-values greater than 0.05 are generally
believed to indicate a good match of the observed distribution with the expected distribution.
As can be seen from the table,
with the one exception of the high-churn extreme-capacity case,
node degrees and selection frequencies closely track the desired
values. The valid p-values are all comfortably greater than 0.05, indicating good
selection distribution.3
In the high-churn extreme capacity case, high degree nodes have an average total degree that is
less than the respective ideal values: High degree nodes
need some time to reach their full degrees upon entering the system, because
they have at most 10 neighbor discovery walks outstanding at any time. This
effect is more prominent during high-churn, where new nodes enter more frequently.
The values for the relative selection frequencies suffer because of the
imperfect degree distribution, but they nevertheless are still reasonably close to
the target ratios.
The message load ratios in the extreme capacity
distribution deviates from the ideal 3:60:150; this is because some
of the high-degree neighbors have duplicate links between them, resulting
in a reduction of the heart-beat load incurred. This is an artifact of the fact
that the total degree of the highest capacity nodes here is non-negligible in
comparison to the total number of links in the system, and we expect the number
of duplicate links to decrease and the load-ratios to get closer to the 3:60:150
proportion in larger networks.
Looking at the message loads from an alternate perspective, the absolute
values of the message loads for the outdegree 60 and outdegree 150 nodes seem relatively
high. The bulk of this load is caused by neighbor heart-beats. In
Section 6.4 we describe how we can reduce this load by doing
heart-beats in a more sophisticated fashion.
We ran similar experiments for 5000 nodes Swaplinks graphs over a 20 CPU cluster on the Emulab
testbed, and found the results to be broadly similar, demonstrating that
Swaplinks retains its properties in larger networks as well.
6.1.2 KRB Results
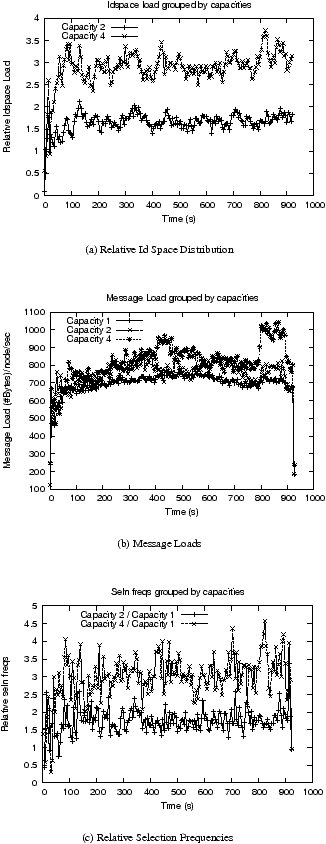
| Figure 3: KRB under high churn and moderate capacity distribution |
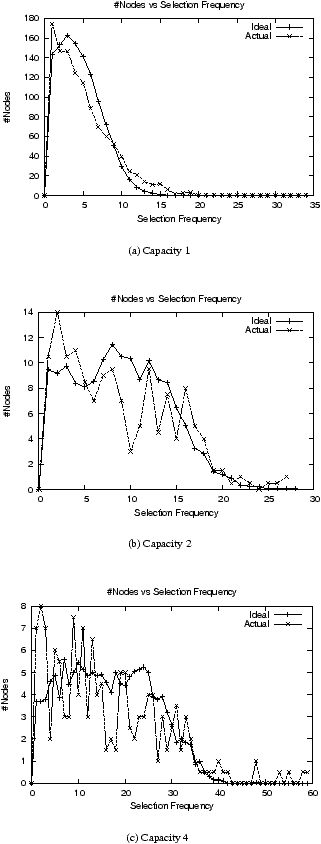
| Figure 4: KRB #Nodes vs Selection Frequency for burst selections:
high churn and moderate capacity distribution |
| | High Churn | Low Churn |
|
Target Split | 1 | 2 | 4 | 1 | 20 | 50 | 1 | 2 | 4 | 1 | 20 | 50 |
|
Idspace Split: | 1 | 1.68 | 2.99 | 1 | 6.14 | 5.89 | 1 | 1.95 | 3.98 | 1 | 23.59 | 37.41 |
|
Msg Load(B/s) | 711.30 | 765.04 | 853.78 | 736.63 | 922.48 | 923.40 | 261.73 | 290.59 | 318.45 | 297.01 | 474.06 | 413.49 |
|
Relative Selns | 1 | 1.78 | 3.13 | 1 | 5.74 | 5.29 | 1 | 1.98 | 4.02 | 1 | 23.23 | 34.44 |
|
Seln p-values | 0.000 | 0.231 | 0.054 | 0.000 | 0.000 | 0.002 | 0.000 | 0.645 | 0.774 | 0.000 | NaN | 0.001 |
|
| Table 2: KRB results for moderate and extreme capacity distributions under high and low churn. |
We make a few changes to the parameters used by the default Bamboo source
distribution to get KRB to approach the desired relative capacity-wise ID space distributions.
For the high-churn results shown in this section, we set ping and leaf-set-alarm
periods in Bamboo to 1 second. We set the near and far routing table alarm
periods to 2.5 and 5 times the leaf-set-alarm respectively (these ratios are
based on the values in Bamboo's code distribution).
We use a period of 5 seconds between successive KRB load messages sent to random
locations in the network (we denote this period the KRB period).
For the low-churn results, we set the ping period to 2 seconds, the leaf-set
alarm period to 3 seconds and the KRB period to 10 seconds.
Bamboo has a time-out value between when a node
suspects a neighbor to be down (as a result of failure of message delivery) to when
it actually decides it's down (as a result of lack of response to pings sent
to the neighbor). We reduce this timeout value to 1 second from the earlier value of 60 seconds.
We use a leaf-set size of 4 and a KRB-threshold value (see Section 5) of 0.2 in all KRB simulations.
We restricted KRB low-churn simulations to a shorter duration of 1800 seconds;
longer simulations took unreasonably longer (wall-clock) times to complete.
Figures 3 and 4, and Table
2 show the results for KRB.
The results show that KRB is not successful in maintaining the relative
ID-spaces at the desired levels under high churns – it is only able to achieve
around a 1:1.65:3 relative division in the ID spaces in the moderate capacity
distribution, while its response to the extreme capacity distribution under high
churn is worse. KRB is able to achieve the desired relative ID-space
distribution in the low-churn moderate-capacity case, but again
fails to fully achieve the desired ID-space distribution in the
extreme-capacity low-churn scenario. KRB also fails to consistently achieve the desired
selection distribution within each capacity class, as seen by the burst
selection p-values computed for the selection
frequencies.
The p-values for the lowest capacity class in the moderate capacity distribution is 0
in both the high and low churn scenarios. This is mainly because the actual selection
distributions here have quite a few outliers – nodes with an actual selection frequency
close to or greater than the maximum selection frequency (for any node)
predicted by the ideal curve. KRB's selection frequency curves within capacity
classes 2 and 4 do match the ideal curve closely enough that they succeed the
p-value test, but during high-churn, nodes in the higher capacity classes are still less
likely to get selected than they should ideally be.

| Figure 5: Change in the universal objective function as a result of KRB node
moves and node churn in a high-churn, moderate-capacity simulation. |
Figure 5 shows why KRB underperforms under high churn: The
system-wide objective function (Equation 3,
Section 5) settles to a more or less stable positive value in
the presence of the steady churn. KRB's attempts to improve the objective
function value below this stable value using node movements are exactly
counterbalanced by the effects of node churn, indicating that this is the best
KRB can do under this high churn.
Increasing the frequency of KRB node movements here does not lead to an
improvement in performance, as becomes clear next.
We evaluated the relative ID-space distribution realized by KRB under high churn and
moderate capacities for various values of the KRB
parameters (ping, alarm, KRB periods, KRB-threshold), and we found that the combination
of the parameters we present here results in the best ID-space distribution. In
general, we found that more frequent pings and alarm messages of Bamboo resulted
in better results (as can be expected), while there generally was an `optimal'
KRB message frequency and an optimal value for the KRB threshold given the frequencies
used for the other messages. Setting
the KRB message frequency to higher values resulted in an increase of the
number of incorrect KRB moves, where nodes switched positions based on an
incorrectly perceived local state, thereby worsening the ID-space distribution.
Among the combinations of parameters we tested, the worst performing
set yielded about 50% less accurate selection than the setting we use.
This experience
indicates that it is harder with KRB to decide on the exact set of various
parameters to use in a general setting.4
KRB achieves a higher average message load (across all nodes) than does
Swaplinks: this is mainly a result of the increased message rates we used to improve KRB's
capacity-based ID space distribution. We however do not think that the message
load values are high enough to be a concern here.
6.2 Extreme churn
We now look at the reaction of Swaplinks and KRB to more extreme churn events,
the first where a flash-crowd leads to the network size doubling from 1000 nodes to
2000 nodes in the span of 10 seconds, and the second
where a half of the network dies instantaneously.
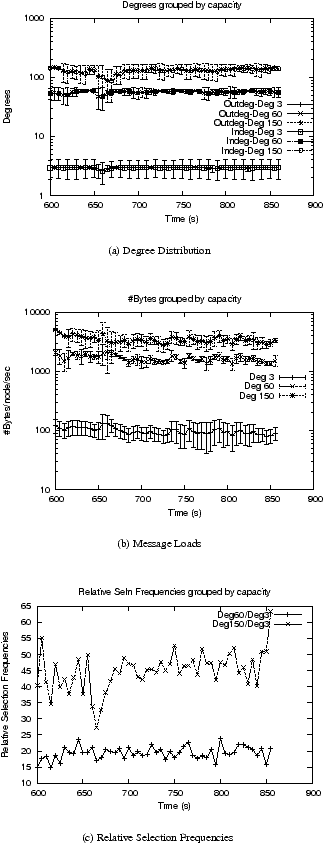
| Figure 6: Swaplinks: Flash-crowd with high churn and extreme capacity distribution |
| | Flash Crowd |
| Target Outdeg | Avg Load(B/s) | Relative Load | Avg Total deg | Relative Selns | Seln p values |
| 5 | 146.88 | 1 | 9.82 | 1 | 0.936 |
| 10 | 291.94 | 1.98 | 19.73 | 2.06 | 0.935 |
| 20 | 578.49 | 3.93 | 39.18 | 4.02 | 0.722 |
| 3 | 91.29 | 1 | 5.9 | 1 | 0.751 |
| 60 | 1553.79 | 17.01 | 114.61 | 19.66 | 0.873 |
| 150 | 3320.49 | 36.34 | 269.54 | 46.94 | 0.567 |
| | Mass Departures |
| 5 | 179.52 | 1 | 9.54 | 1 | 0.457 |
| 10 | 351.01 | 1.95 | 19.11 | 2.04 | 0.912 |
| 20 | 681.62 | 3.79 | 37.59 | 3.96 | 0.988 |
| 3 | 121.57 | 1 | 5.73 | 1 | 0.338 |
| 60 | 1886.01 | 15.5 | 102.19 | 17.87 | 0.418 |
| 150 | 4343.61 | 35.66 | 251.1 | 45.84 | NaN |
| Table 3: Swaplinks performance with flash-crowds and mass departures under
high churn. |
Figure 6 shows the results of the Swaplinks flash-crowd scenario under a
3:60:150 degree distribution under high-churn (a median node session time of 2
minutes).
The flash-crowd appears in the period 650-660 seconds after the system is
started, and two sets of burst-selections are performed starting at 723 seconds
and spanning 100 seconds.
Table 3 summarizes the flash-crowd results over the last
175 seconds of the experiment for both the moderate and extreme capacity
distributions. Figure 6 shows that while there is a temporary deterioration in all the metrics of interest for a short
duration of time immediately after the entry of the flash-crowd, the system quickly recovers to re-establish
desired behavior.
The Swaplinks graph in fact generally benefits from nodes entering the system,
since this pushes the average degree distribution across the graph towards the ideal
value; a comparison of
Table 3
with
Table 1
shows that the average values for the degree and relative selection frequencies
in fact improve as a result of the arrival of the flash-crowd!
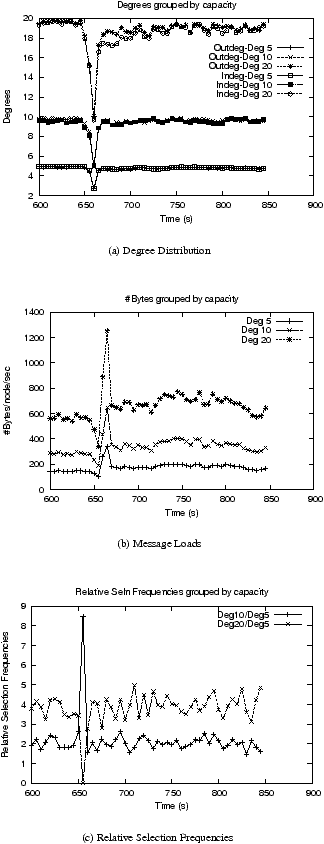
| Figure 7: Swaplinks: Mass departures with high churn and moderate capacity distribution |
Figure 7 and Table 3 show results of the Swaplinks mass
departure experiments.
The mass departures occur at 649 seconds after system start, and burst selections are performed at 719 seconds after system start.
From figure 7 (for high churn and moderate
capacity distributions), we
observe that the network suffers for a short
duration of time immediately after the huge perturbation, but things start to
improve thereafter. The message loads and the selection frequencies recover to
re-approach the desired 1:2:4 split of message loads and selection frequencies.
The extreme capacity results from Table 3 also look
encouraging: the degrees and the relative selection frequencies are
similar to the high (stable) churn, extreme-capacity results shown earlier in
Table 1.
Overall, these experiments demonstrate that Swaplinks is robust to various kinds
of network churn under widely different capacity distributions, and that it manages
to retain its fine-grained sensitivity to the desired heterogeneity under these
conditions.
| | Flash-crowd | Mass Departures |
| Target Split | 1 | 2 | 4 | 1 | 2 | 4 |
| Idspace Loads | 1 | 1.52 | 2.41 | 1 | 1.19 | 1.68 |
| Relative Selns | 1 | 1.55 | 2.47 | 1 | 1.14 | 1.75 |
| Seln p-values | 0.00 | 0.00 | 0.01 | 0.00 | 0.48 | 0.00 |
| Table 4: KRB Results for flash-crowds and mass departures for moderate capacity distributions and high churn |
Table 4 summarizes KRB results from the last 175
seconds of the flash-crowd
and the mass departure simulations for only the moderate capacity distribution under
high churn. The flash-crowds and mass departures occur at the same times as
those reported in the Swaplinks experiments.
The results indicate that the KRB performance suffers significantly as a result of the
extreme churn induced. The relative ID-spaces and selection frequencies differ
markedly from the target values, resulting in a failure to realize the
desired selection distribution. We noticed that while KRB had started to recover
from the flash-crowd to approach its stable ID-space distribution towards the
end of the simulation, in the mass departure simulation its stable ID-space distribution
deteriorated after the mass departures, leading to worse relative selection
values at the end of the simulation. 5
Since we have already seen that KRB fails to adapt to the extreme-capacity
setting under high churn, we do not subject it to the more demanding
circumstances of both extreme churn (mass departures and flash crowds) and extreme
heterogeneity.
6.3 Evaluation over PlanetLab
We evaluated Swaplinks over PlanetLab by deploying a
250-node network over 50 PlanetLab hosts distributed across the world. We scaled
down the number of selections performed in the burst mode here to about 2500.
| | High Churn | Low Churn |
|
Target Outdeg | 5 | 10 | 20 | 5 | 10 | 20 |
|
Avg Load(B/s) | 210.88 | 418.36 | 794.16 | 196.81 | 384.10 | 745.75 |
|
Load split | 1 | 1.97 | 3.76 | 1 | 1.95 | 3.76 |
|
TotalDeg | 9.54 | 19.15 | 37.46 | 10.04 | 19.79 | 39.48 |
|
Relative Selns | 1 | 2.07 | 3.99 | 1 | 2.01 | 3.94 |
|
Seln p-values | 0.000 | 0.000 | 0.001 | 0.000 | 0.023 | 0.002 |
|
| Table 5: PlanetLab results with moderate capacity distribution |
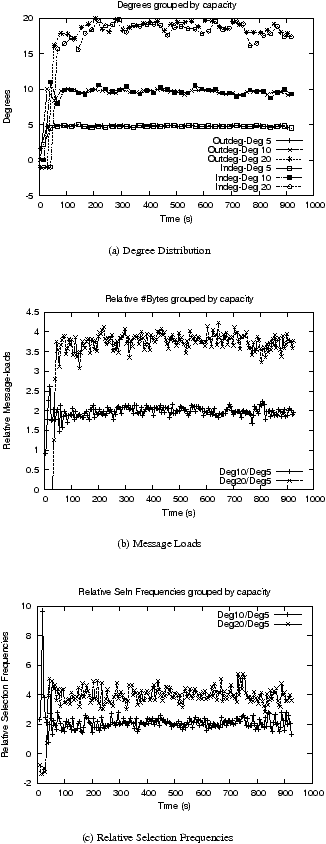
| Figure 8: PlanetLab 250 nodes with high churn and moderate capacity distribution |
Figure 8 shows the variation of average node degrees, message
loads and the relative selection frequencies with time in a high-churn moderate
capacity experiment
, and Table 5 summarizes both the
high-churn and low-churn experiments.
While the node-degree curve in the high churn case is not
completely stable, due to the high
churn, all the values nevertheless adhere reasonably closely to the
desired 5:10:20 ratio. But there is a gap between the ideal distribution of
#Nodes vs Selection Frequencies and the actual distribution here, leading to poor
p-values for the selection distribution. We observed that a few of the planetlab
nodes hosting our experiments appeared to freeze occasionally, causing the
Swaplinks instances hosted on these nodes to be eventually excluded from the neighbor-sets
of other Swaplinks instances. This also means that such nodes would not be
selected by any subsequently launched random selection walk, thus causing the
discrepancy between the actual and observed selection distributions.
We do not show results for the extreme capacity distribution here:
the fact that each high capacity class constitutes just 1% of the total node
population means that there would be too
few high capacity nodes in a 250-node experiment to draw reliable conclusions.
6.4 Smart-Pinging
The bulk of the message load seen by Swaplinks nodes is from
the heart-beat messages used to determine when a neighbor is down.
We would like to minimize this load, in part because in extreme
heterogeneity situations some nodes have many neighbors, but in
part because a given application might result in a computer belonging
to many P2P networks, and therefore have many neighbors.
Our basic approach to minimizing heart-beats is as follows:
Rather than have every neighbor determine for itself whether a node A
is down, one neighbor (at a time) determines if a node A is down.
If a neighbor determines that node A is down, it informs the other neighbors
of node A, using a flood, that node A is down. Specifically, the smart-pinging scheme we designed works as follows:
Node A tells each of its neighbors about some random set of its other neighbors, such
that each neighbor is known by at least some small number of other neighbors.
Node A sends each neighbor in turn a small series of (say five) heart-beat
messages, each spread two seconds apart.
For example, node A sends neighbor 1 five heartbeats, neighbor 2 five
heartbeats, and so on.
Each neighbor knows when to expect its series of heartbeats, based on
timing information conveyed during the previous series of heartbeats.
If a neighbor misses all of its heartbeats, it informs all the neighbors
of A it knows of that node A is down. These neighbors in turn inform the
neighbors they know, and the ensuing flood of packets quickly informs
all neighbors that node A is down.6 Smart-pinging reduces the amount of bandwidth consumed under no churn, at the
cost of a burst of messages that occurs when there is churn, and the possibility
of incorrect notifications of node departure.
While we need to explore these trade-offs in greater detail,
we have currently implemented a preliminary version of smart-pinging,
and observe that it does indeed
result in a saving on message load under low-churn scenarios.
In the current implementation, if node A has d out-neighbors, A
has each of its neighbors know of 2 log2(d) of its (A's) neighbors.
Table 6 summarizes the results over the second half of the
duration of the experiment.
This experiment was run
with just 8 periodic selectors (instead of 80 as in the
previous cases), to isolate the heart-beat load.
| Target Outdeg | 5 | 10 | 20 |
| Avg Load (B/s) | 38.23 | 57.97 | 89.21 |
| Relative Load | 1 | 1.50 | 2.30 |
| Avg Totaldeg | 9.99 | 19.90 | 40.01 |
| Relative Selns | 1 | 2.06 | 4.08 |
| Seln p-values | 0.831 | 0.904 | 0.877 |
| Table 6: Smart Pinging: moderate capacity, low churn |
7 Conclusions
Node heterogeneity, where different nodes have different capacities, is an important issue in current peer-to-peer systems.
In this paper, we provide the implementation and performance evaluation of the Swaplinks heterogeneous graph construction and peer selection mechanism.
We also compare its heterogeneous selection properties with that of KRB,
a structured P2P approach derived by adapting the Karger-Ruhl load-balancing
scheme to node ID spaces in the Bamboo DHT.
We find that while Swaplinks generally gives good performance along all
metrics of interest, KRB finds it hard, under relatively high churn rates, to
maintain the desired selection probabilities even for moderate distributions
in desired selection probabilities. Also, with KRB, it is non-trivial to zero
in on a good set of tuning parameters to use in a general setting. Overall, we
find that Swaplinks outperforms KRB in performing heterogeneity-sensitive
random peer selection.
In terms of enhancements to Swaplinks, we need to experiment further
with smart-pinging, for instance to insure that it doesn't suffer from
false negatives. In addition, we note that Swaplinks discovers truly
random neighbors. Some P2P applications, however, would like to also
discover neighbors that are nearby in terms of latency. While a P2P
application is free to do that on its own (i.e. by using Swaplinks to
discover random peers, and then measuring latency to them), we believe
that it would beneficial to explore efficient ways to do this, and
add the capability to the Swaplinks toolkit.
A limitation of Swaplinks is that it has no defense against
misbehaving nodes. For instance, if a node wished to obtain a huge
number of neighbors (for instance to DoS a file-sharing application),
Swaplinks has no mechanism to prevent this. While we are interested
in exploring such mechanisms,
Swaplinks is currently only appropriate for use with trusted P2P software.
We are currently exercising Swaplinks by using it as a basis for a number of
P2P applications:
The Swaplinks toolkit is being used as the basis for the Chunkyspread
P2P multicast system [7]. In addition, the Swaplinks algorithm
is being used in building a toolkit for NAT traversal in P2P
applications, and a P2P file backup system. We invite researchers to use our
Swaplinks toolkit in their unstructured P2P applications [16].
8 Acknowledgments
We would like to thank Grant Goodale and Victoria Krafft for help in adapting
the Bamboo simulator to KRB.
References
[1]
Paul Francis.
Yoid: Extending the internet multicast architecture.
In Unrefereed report, 2000.[2]
D. Kostic, A. Rodriguez, J. Albrecht, and A. Vahdat.
Bullet: High bandwidth data dissemination using an overlay mesh.
In Proc. ACM SOSP, 2003.[3]
Vinay Pai, Kapil Kumar, Karthik Tamilmani, Vinay Sambamurthy, and Alexander E.
Mohr.
Chainsaw: Eliminating trees from overlay multicast.
In Proc. IPTPS, 2005.[4]
Yatin Chawathe, Sylvia Ratnasamy, Lee Breslau, Nick Lanham, and Scott Shenker.
Making gnutella-like p2p systems scalable.
In Proc. ACM SIGCOMM, 2003.[5]
Frank Dabek, Russ Cox, Frans Kaashoek, and Robert Morris.
Vivaldi: A decentralized network coordinate system.
In Proc. ACM SIGCOMM, 2004.[6]
Li wei Lehman and Steven Lerman.
Palm: Predicting internet network distances using peer-to-peer
measurements.
In Technical Report, MIT, 2004.[7]
Vidhyashankar Venkataraman and Paul Francis.
Chunkyspread: Heterogeneous unstructured tree-based peer to peer
multicast.
In Proc. ICNP, 2006.[8]
Yang hua Chu, Aditya Ganjam, T. S. Eugene Ng, Sanjay G. Rao, Kunwadee
Sripanidkulchai, Jibin Zhan, and Hui Zhang.
Early deployment experience with an overlay based internet
broadcasting system.
In Proc. USENIX Annual Technical Conference, 2004.[9]
A. Bharambe, S. Rao, V. Padmanabhan, S. Seshan, and H. Zhang.
The impact of heterogeneous bandwidth constraints on dht-based
multicast protocols.
In Proc. IPTPS, 2005.[10]
M. Castro, P. Druschel, A. Kermarrec, A. Nandi, A. Rowstron, , and A. Singh.
Splitstream: High-bandwidth content distribution in cooperative
environments.
In Proc. ACM SOSP, 2003.[11]
Vivek Vishnumurthy and Paul Francis.
On heterogeneous overlay construction and random node selection in
unstructured p2p networks.
In Proc. IEEE Infocom, 2006.[12]
David R. Karger and Matthias Ruhl.
Simple efficient load balancing algorithms for peer-to-peer systems.
In Proc. IPTPS, 2004.[13]
S. Rhea, D. Geels, T. Roscoe, and J. Kubiatowicz.
Handling churn in a dht.
In Proc. USENIX Annual Technical Conference, 2004.[14]
I. Stoica, R. Morris, D. Karger, F. Kaashoek, and H. Balakrishnan.
Chord: A scalable peer-to-peer lookup service for internet
applications.
In Proc. ACM SIGCOMM, 2001.[15]
A. Rowstron and P. Druschel.
Pastry: Scalable, distributed object location and routing for
large-scale peer-to-peer systems.
In Proc. IFIP/ACM Middleware, 2001.[16]
https://www.cs.cornell.edu/%7evivi/research/swaplinks.html.[17]
Sylvia Ratnasamy, Paul Francis, Mark Handley, Richard Karp, and Scott Shenker.
A scalable content-addressable network.
In Proc. ACM SIGCOMM 2001, 2001.[18]
David Karger, Eric Lehman, Tom Leighton, Mathhew Levine, Daniel Lewin, and Rina
Panigrahy.
Consistent hashing and random trees: Distributed caching protocols
for relieving hot spots on the world wide web.
In Proc. ACM STOC, 1997.[19]
Frank Dabek, M. Frans Kaashoek, David Karger, Robert Morris, and Ion Stoica.
Wide-area cooperative storage with CFS.
In Proc. SOSP, 2001.[20]
Ananth Rao, Karthik Lakshminarayanan, Sonesh Surana, Richard M. Karp, and Ion
Stoica.
Load balancing in structured p2p systems.
In IPTPS, 2003.[21]
P. Brighten Godfrey and Ion Stoica.
Distributed construction of random expander networks.
In Proc. IEEE Infocom, 2005.[22]
Jonathan Ledlie and Margo Seltzer.
Distributed, secure load balancing with skew, heterogeneity, and
churn.
In Proc. IEEE Infocom, 2005.[23]
Jinyang Li, Jeremy Stribling, Robert Morris, and M. Frans Kaashoek.
Bandwidth-efficient management of DHT routing tables.
In Proc. NSDI, 2005.[24]
Miguel Castro, Manuel Costa, and Antony Rowstron.
Debunking some myths about structured and unstructured overlays.
In Proc. NSDI, 2005.[25]
David R. Karger and Matthias Ruhl.
New algorithms for load balancing in peer-to-peer systems.
In IRIS Student Workshop (ISW '03), 2003.[26]
Roie Melamed and Idit Keidar.
Araneola: A scalable reliable multicast system for dynamic
environments.
In Proc. NCA 2004, 2004.[27]
C. Law and K.-Y. Siu.
Distributed construction of random expander networks.
In Proc. IEEE Infocom, 2003.[28]
Ayalvadi J. Ganesh, Anne-Marie Kermarrec, and Laurent Massoulie.
Scamp: peer-to-peer lightweight membership service for large-scale
group communication.
In Proc. 3rd Intnl. Wshop Networked Group Communication (NGC
'01), pages 44–55, 2001.[29]
D. Kostic, A. Rodriguez, J. Albrecht, A. Bhirud, and A. Vahdat.
Using random subsets to build scalable network services.
In Proc. USITS, 2003.[30]
N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, and E. Teller.
Equations of state calculations by fast computing machines.
In Journal of Chemical Physics, 1953.[31]
I Csiszár.
Information theoretic methods in probability and statistics.
In IEEE Information Theory Society Newsletter 48, 1998.[32]
Saikat Guha and Paul Francis.
Towards a Secure Internet Architecture Through Signaling.
Technical Report cul.cis/TR2006-2037, Cornell University, 2006.[33]
Ellen W. Zegura, Kenneth L. Calvert, and Samrat Bhattacharjee.
How to model an internetwork.
In Proc. IEEE Infocom, 1996.[34]
Subhabrata Sen and Jia Wang.
Analyzing peer-to-peer traffic across large networks.
In Second Annual ACM Internet Measurement Workshop, 2002.[35]
S. Saroiu, P. Gummadi, and S. Gribble.
A measurement study of peer-to-peer file sharing systems.
In Proc. MMCN, 2002.[36]
K. Gummadi, R. Dunn, S. Saroiu, S. Gribble, H. Levy, and J. Zahorjan.
Measurement, modeling, and analysis of a peer-to-peer file-sharing
workload.
In Proc. ACM SOSP, 2003.[37]
Miguel Castro, Manuel Costa, and Antony Rowstron.
Should we build gnutella on a structured overlay?
In Proc. HotNets-II, 2003.
This document was translated from LATEX by
HEVEA.
|
