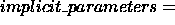
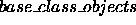

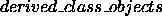




McGregor and Dyer[18] considered the inheritance relationship between two classes as a mapping that carries out certain transforms on attributes as they are inherited from one class to another. Each object-oriented language has its own set of transforms that may be applied.
This means that the attributes that are visible to the methods of the derived class are a subset of the attributes from the base class. The visibility component calculation therefore has to be modified to handle this.
In the case of C++, all of the protected and public attributes of the base class are visible to the derived class. This increases the set of data objects that are visible to the methods in the derived class. Other languages have different visibility and scoping rules, like the implicit private area in Smalltalk objects, and encapsulation mechanisms such as packages in Java. We therefore consider the set of implicit parameters in the derived class to include all the objects from the base class that are visible in the derived class.
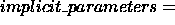
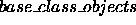

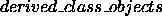
These modifications also make the metric sensitive to the level of inheritance in the class hierarchy. Since the implicit parameter calculation is influenced only by the visibility level (i.e private, public or protected) of the objects in the base class rather than the class of the object, the metric is monotonically increasing. To address this issue, we have assumed that the count of the implicit parameters of a class at any level in the inheritance graph includes the protected/public attributes of all the classes that lie above it in the inheritance tree. If a class multiply inherits from many classes, the count of the implicit parameters that inherit from this class, increases substantially. This demonstrates that misuse of multiple inheritance could lead to potential problems in maintainance and testing.
The above counting rules also make the metric compatible with the DIT metric proposed by Chidamber[5]. The deeper a class in the hierarchy, the greater is the number of data objects it is likely to inherit, making it more complex to test.


