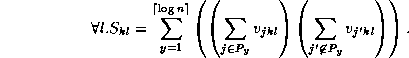

Thew auctioneers now compute
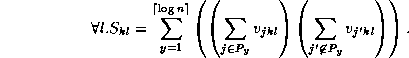
The inner summations may be performed without communication. Simple
dynamic programming can be used to perform these summations in
![]() additions (of points in the field
additions (of points in the field ![]() ). The
). The
![]() multiplications require a degree reduction
step on these
multiplications require a degree reduction
step on these ![]() products. The outer summations
may then be performed with
products. The outer summations
may then be performed with ![]() field
additions and no communication.
field
additions and no communication.
The outer summation runs over the indices for the partitions. The
inner summations run over all j in each half of a particular
partition. These summations act like a logical OR operation over one
side of the partition. In other words, if the partition side contains
one or more bids which are at least as high as the test value, then
the evaluation of this sum at 0 will be non-zero. For the polynomial
result of multiplying the two inner summations, the evaluation at 0
will be non-zero only when the there is at least one bid on each side
of the partition which is as high as the test bid. From this it is
clear that no summand in the outer summation will have a value at 0
which is non-zero unless there are at least two bids which are at
least as high as the test value. Conversely, we chose the partitions
such that some partition would separate any pair ![]() , so if there
are two bids which are greater than the test bid, then at least one
summand has a value at 0 which is non-zero. This means that (with high
probability, see section 4.8)
, so if there
are two bids which are greater than the test bid, then at least one
summand has a value at 0 which is non-zero. This means that (with high
probability, see section 4.8) ![]() will be non-zero
if and only if there are at least two bids at least as high as the
test bid, or, equivalently, that the selling price is at least as high
as the test bid.
will be non-zero
if and only if there are at least two bids at least as high as the
test bid, or, equivalently, that the selling price is at least as high
as the test bid.
By this stage, the auctioneers must have agreed on two further shared
polynomials for each value of l: one of degree t (call it
![]() ) which is selected uniformly randomly from
) which is selected uniformly randomly from ![]() and one
of degree 2t (call it
and one
of degree 2t (call it ![]() ) which is selected to be uniformly
random up to the constraint that its value at 0 is 0. The k
subscript is used to indicate that different polynomials should be
chosen for each round. Since they are dependent only on m, c, and
p, the
) which is selected to be uniformly
random up to the constraint that its value at 0 is 0. The k
subscript is used to indicate that different polynomials should be
chosen for each round. Since they are dependent only on m, c, and
p, the ![]() and
and ![]() may be generated in batches and used
over the course of many auctions.
may be generated in batches and used
over the course of many auctions.
The auctioneers compute ![]() .
This computation has no influence on the determination of the winner
or selling price. Rather, it is necessary to preserve secrecy of the
bids when
.
This computation has no influence on the determination of the winner
or selling price. Rather, it is necessary to preserve secrecy of the
bids when ![]() is revealed. The need for this step is not
entirely theoretical; if it is not performed, there is an
attack by a combination of an auctioneer and some bidders which could
potentially reveal certain information about competing bids. Revealing
is revealed. The need for this step is not
entirely theoretical; if it is not performed, there is an
attack by a combination of an auctioneer and some bidders which could
potentially reveal certain information about competing bids. Revealing
![]() indicates only whether
indicates only whether ![]() is zero or non-zero, which
is exactly the information we will use to decide the
is zero or non-zero, which
is exactly the information we will use to decide the ![]() digit of
the selling price.
digit of
the selling price.
Now, the secrets of these ![]() are computed by the auctioneers
(i.e., the values
are computed by the auctioneers
(i.e., the values ![]() ). Let
). Let ![]() be the the
largest value of l for which
be the the
largest value of l for which ![]() (
( ![]() if
if ![]() for all l). The
for all l). The ![]() digit of the bid is now set equal to
digit of the bid is now set equal to ![]() (i.e.
(i.e. ![]() ).
).