


Next: Secret computation
Up: Introduction
Previous: Introduction
How do existing auction types stack up against our desiderata?
Consider these three broad categories of auctions that have been proposed:
- Increasing-price auction (English auction). In this type
of auction, a good or commodity is offered at increasing prices. It
may initially be offered at K tokens; at successive points of time
i it is bid at
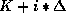 tokens (
tokens ( 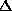 may be a function
of previous bids and other factors). At each unit of time, one or
more parties can bid for the item. At the end of the auction, the
highest bidder takes the item; he pays the price he bid. This is
the sort of auction found at Sotheby's and Christie's. This type of
auction has many disadvantages: the time necessary to conduct the
auction is potentially proportional to the price at which the item
is sold; the communication costs may grow super-linearly in the
ultimate price at which the item is sold (since at lower prices,
multiple bidders may simultaneously bid for an item); moreover, this
type of auction leaks an enormous amount of information--a careful
observer will be able to deduce information about the price that
each party is willing to pay for the auctioned good. However, the
auction does have a very desirable feature: in economic terms, it
allocates the good to the bidder with the highest valuation, since
the bidder with the highest valuation will be willing to outbid all
other bidders.
may be a function
of previous bids and other factors). At each unit of time, one or
more parties can bid for the item. At the end of the auction, the
highest bidder takes the item; he pays the price he bid. This is
the sort of auction found at Sotheby's and Christie's. This type of
auction has many disadvantages: the time necessary to conduct the
auction is potentially proportional to the price at which the item
is sold; the communication costs may grow super-linearly in the
ultimate price at which the item is sold (since at lower prices,
multiple bidders may simultaneously bid for an item); moreover, this
type of auction leaks an enormous amount of information--a careful
observer will be able to deduce information about the price that
each party is willing to pay for the auctioned good. However, the
auction does have a very desirable feature: in economic terms, it
allocates the good to the bidder with the highest valuation, since
the bidder with the highest valuation will be willing to outbid all
other bidders.
- Sealed-bid auctions. In this type of auction, each party
sends a sealed bid to an auctioneer who opens all bids. The
auctioneer determines the highest bid and sells the item to that
bidder for the bidding price. This type of auction can execute in a
single round of communication between the bidders and the
auctioneers. However, it has disadvantages. First, the auctioneer
will know the exact price that each party is willing to pay.
Second, it does not support optimal distribution of goods.
In a sealed bid auction, participants will have beliefs about what
others will bid. If a participant believes that she will have the
highest bid, and the second highest bid will be substantially
beneath that, then she has an incentive to lower her bid. For
example, if she values an item at $1,000, but believes that the
second highest bidder values the item at $500, then she is likely
to place a bid slightly higher than $500. If she is wrong about
the distribution of other bids, then the final item will not go to
the party that values it most, and the seller will have given up the
item a price lower than he would have achieved with an English
auction. [9, 11, 13, 14].
- Decreasing-price auction (Dutch auction). This type of
auction is similar to the English auction in that the bidding price
varies over time; however, in this case, the price decreases and at
time i is
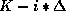 . The first bidder will take the item.
This type of auction has the advantage of preserving maximum privacy
-- no information is revealed except the winning bid and bidder;
however like the increasing-price auction, it may be time consuming,
and like the sealed-bid auction, it is not economically
efficient [9, 11, 13, 14].
. The first bidder will take the item.
This type of auction has the advantage of preserving maximum privacy
-- no information is revealed except the winning bid and bidder;
however like the increasing-price auction, it may be time consuming,
and like the sealed-bid auction, it is not economically
efficient [9, 11, 13, 14].
In Nobel-prize winning work, the economist Vickrey designed a type of
auction that combined the best features of an increasing-price auction
and a sealed-bid auction [13]. Vickrey's technique, called
a second-price auction, works like a sealed-bid auction, in that
all bids are sealed and sent to an auctioneer. Like a sealed bid
auction, the highest bidder wins. But the price the winner pays is
the price that the second highest bidder has bid. For example,
suppose that we bid 100 tokens and the second highest bid is 10
tokens. Then we will win the bid, but we will only have to pay 10
tokens to secure the good. This auction runs in constant time, and
maximizes consumer surplus, but it is still highly centralized and
does not protect the privacy of the bids.
The main contribution of this paper is to give a private-bid version
of a second-price auction. This auction
- will run in a single round of bid submissions (like a sealed-bid
auction),
- is efficient enough for practical implementation,
- will maximize consumer surplus and will give incentives for
participants to submit bids at their true valuations (like an
English auction), and
- will preserve bid privacy (like a Dutch auction).
This is quite an unusual result. In the end, only the second highest bid is
revealed -- the auctioneers and participants (except for the winner) will be
completely unaware of the numerical value of the highest bid (or any
other bid besides the second highest).


Next: Secret computation
Up: Introduction
Previous: Introduction
Doug Tygar
Wed Jul 22 10:16:16 EDT 1998
