



Next: A sample application and
Up: Defining a Safety Policy
Previous: Defining a Safety Policy
Because the experiments in this paper use the DEC Alpha assembly language, our
abstract machine is essentially a high-level formal description of the Alpha
architecture [19]. To see how this is done, consider the subset of
the Alpha instruction set shown in lang. (Actually, we use a
larger subset of the DEC Alpha assembly language in our experiments, but this
smaller subset will suffice for presentation purposes.) In this table, n
denotes an integer constant and  refers to machine register i. All
instructions operate on 64-bit values. For simplicity we allow the use of only
11 temporary and caller-save machine registers (which, for the purpose of this
presentation, we rename
refers to machine register i. All
instructions operate on 64-bit values. For simplicity we allow the use of only
11 temporary and caller-save machine registers (which, for the purpose of this
presentation, we rename 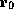 through
through 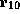 ). The consequence of this
is that programs cannot write into reserved and callee-save registers
(according to the standard C calling convention for the DEC Alpha
architecture), and are thus trivially safe with respect to these registers.
). The consequence of this
is that programs cannot write into reserved and callee-save registers
(according to the standard C calling convention for the DEC Alpha
architecture), and are thus trivially safe with respect to these registers.
To define how programs are executed, we define an abstract machine as a
state-transition function, the essential core of which is shown in
abs-mach. In this specification, the DEC Alpha program is a
vector of instructions,  , and the current instruction is
, and the current instruction is  ,
where
,
where  is the program counter. The variable
is the program counter. The variable  denotes the state of
the machine registers and memory. The state-transition function maps a machine
state
denotes the state of
the machine registers and memory. The state-transition function maps a machine
state 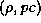 into a new state
into a new state  by executing the current
instruction
by executing the current
instruction 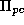 .
.
The notation 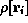 (often abbreviated as
(often abbreviated as  ) refers to the value
of register
) refers to the value
of register 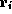 in state
in state  .
. The expression
The expression 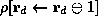 denotes
the new state obtained from state
denotes
the new state obtained from state  by incrementing the value of register
by incrementing the value of register
 . So, for example, the Alpha ``
. So, for example, the Alpha ``  ''
instruction is defined by abs-mach to have the following semantics:
[
([d s op], + 1)
]
where
''
instruction is defined by abs-mach to have the following semantics:
[
([d s op], + 1)
]
where  is the current register and memory state. This
specification states that the ADDQ instruction updates register
is the current register and memory state. This
specification states that the ADDQ instruction updates register 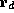 with the sum of
with the sum of 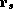 and op, and also increments the program counter.
We use the ``circled'' operation
and op, and also increments the program counter.
We use the ``circled'' operation  to denote two's-complement
addition on 64 bits. This operation is defined in terms of the usual integer
arithmetic operations as
to denote two's-complement
addition on 64 bits. This operation is defined in terms of the usual integer
arithmetic operations as


: The Abstract Machine.
To model the state of memory, we use a pseudo register, called  , that
gives the content of each memory location. We write
, that
gives the content of each memory location. We write  for the
contents of memory address a, and
for the
contents of memory address a, and  for the
new memory state resulted from writing register
for the
new memory state resulted from writing register  to address a. Memory
operations work on 64-bits and the addresses involved must be aligned on an
8-byte boundary.
to address a. Memory
operations work on 64-bits and the addresses involved must be aligned on an
8-byte boundary.
In the definition of the load and store instructions, there is a crucial
difference between the DEC Alpha processor and our abstract machine. The
difference is that our abstract machine performs the safety checks that are
shown in boxes in abs-mach. For example, consider the definition
of the `` 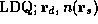 '' instruction:
[
([d s n], + 1),; if;
'' instruction:
[
([d s n], + 1),; if;
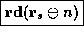 ]
The predicate
]
The predicate 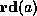 is true when it is safe to read the word at memory
address a, which for the DEC Alpha implies that a is aligned on an 8-byte
boundary. Similarly, the predicate
is true when it is safe to read the word at memory
address a, which for the DEC Alpha implies that a is aligned on an 8-byte
boundary. Similarly, the predicate 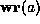 is true when the address a
denotes an aligned location that can be safely read or written. In essence,
these checks define what is meant by safety, and more specifically for this
example, memory safety. For the purpose of this paper, the predicates
is true when the address a
denotes an aligned location that can be safely read or written. In essence,
these checks define what is meant by safety, and more specifically for this
example, memory safety. For the purpose of this paper, the predicates
 and
and  are defined by the safety policy through the
precondition, as shown in the next subsection.
are defined by the safety policy through the
precondition, as shown in the next subsection.
Mathematically, the abstract machine does not return errors when a  or
or  check fails. Instead, the execution blocks because there are no
transition rules covering the error cases. In this setting, a program is safe
if and only if it runs without blocking on the abstract machine. Of course, the
presence of these safety checks means that the abstract machine is not a
faithful abstraction of the DEC Alpha processor. However, the purpose of
certification is to prove that all safety checks always succeed. If we have a
valid safety proof for a program, we know that we can safely execute it on a
real DEC Alpha and get the same behavior as on our abstract machine, even
though the Alpha does not implement the safety checks.
check fails. Instead, the execution blocks because there are no
transition rules covering the error cases. In this setting, a program is safe
if and only if it runs without blocking on the abstract machine. Of course, the
presence of these safety checks means that the abstract machine is not a
faithful abstraction of the DEC Alpha processor. However, the purpose of
certification is to prove that all safety checks always succeed. If we have a
valid safety proof for a program, we know that we can safely execute it on a
real DEC Alpha and get the same behavior as on our abstract machine, even
though the Alpha does not implement the safety checks.
There are other notable differences between our abstract machine and a real DEC
Alpha. For example, to simplify the presentation in this paper, we have
restricted all branches to be only forward. Allowing backward branches and
loops introduces a number of complications, but is handled in a conceptually
straightforward manner through the addition of explicit loop invariants. As it
turns out, the packet filter examples we use in our experiments do not have any
loops, and so it is not inconvenient to eliminate them here. In a later section
we will briefly describe our experiments with looping programs, including a
safe IP-header checksum routine.

: The Verification-Condition Generator.
Another interesting aspect of the abstract machine is the level of abstraction
of our specification. We might try to be ambitious and make a complete
specification of the DEC Alpha processor. However, this would be extremely
complex and probably difficult to trust. And, as a practical matter, for
specific tasks such as the ones we are considering, many details and features
of the Alpha are irrelevant. This justifies working at a higher level of
abstraction above the details of the pipeline, cache, timing, and interrupt
behavior.
We can also consider encoding other kinds of safety checks into our abstract
machine. For the sake of simplicity, we have specified only a notion of
fine-grained memory safety. With some ingenuity, an abstract machine designer
can define safety policies involving other kinds of safety, like control over
resource usage or preservation of data-abstraction boundaries. Once a safety
policy is defined, application writers are free to use it to create
binaries that guarantee safety.



Next: A sample application and
Up: Defining a Safety Policy
Previous: Defining a Safety Policy
Peter Lee
Tue Sep 17 15:37:44 EDT 1996
 refers to machine register i. All
instructions operate on 64-bit values. For simplicity we allow the use of only
11 temporary and caller-save machine registers (which, for the purpose of this
presentation, we rename
refers to machine register i. All
instructions operate on 64-bit values. For simplicity we allow the use of only
11 temporary and caller-save machine registers (which, for the purpose of this
presentation, we rename 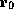 through
through 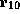 ). The consequence of this
is that programs cannot write into reserved and callee-save registers
(according to the standard C calling convention for the DEC Alpha
architecture), and are thus trivially safe with respect to these registers.
). The consequence of this
is that programs cannot write into reserved and callee-save registers
(according to the standard C calling convention for the DEC Alpha
architecture), and are thus trivially safe with respect to these registers.

 , and the current instruction is
, and the current instruction is  ,
where
,
where  is the program counter. The variable
is the program counter. The variable  denotes the state of
the machine registers and memory. The state-transition function maps a machine
state
denotes the state of
the machine registers and memory. The state-transition function maps a machine
state 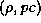 into a new state
into a new state  by executing the current
instruction
by executing the current
instruction 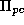 .
.
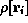 (often abbreviated as
(often abbreviated as  ) refers to the value
of register
) refers to the value
of register 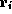 in state
in state  .
.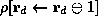 denotes
the new state obtained from state
denotes
the new state obtained from state  by incrementing the value of register
by incrementing the value of register
 . So, for example, the Alpha ``
. So, for example, the Alpha ``  ''
instruction is defined by abs-mach to have the following semantics:
[
([d s op], + 1)
]
where
''
instruction is defined by abs-mach to have the following semantics:
[
([d s op], + 1)
]
where  is the current register and memory state. This
specification states that the ADDQ instruction updates register
is the current register and memory state. This
specification states that the ADDQ instruction updates register 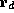 with the sum of
with the sum of 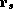 and op, and also increments the program counter.
We use the ``circled'' operation
and op, and also increments the program counter.
We use the ``circled'' operation  to denote two's-complement
addition on 64 bits. This operation is defined in terms of the usual integer
arithmetic operations as
to denote two's-complement
addition on 64 bits. This operation is defined in terms of the usual integer
arithmetic operations as

 , that
gives the content of each memory location. We write
, that
gives the content of each memory location. We write  for the
contents of memory address a, and
for the
contents of memory address a, and  for the
new memory state resulted from writing register
for the
new memory state resulted from writing register  to address a. Memory
operations work on 64-bits and the addresses involved must be aligned on an
8-byte boundary.
to address a. Memory
operations work on 64-bits and the addresses involved must be aligned on an
8-byte boundary.
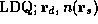 '' instruction:
[
([d s n], + 1),; if;
'' instruction:
[
([d s n], + 1),; if;
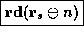 ]
The predicate
]
The predicate 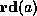 is true when it is safe to read the word at memory
address a, which for the DEC Alpha implies that a is aligned on an 8-byte
boundary. Similarly, the predicate
is true when it is safe to read the word at memory
address a, which for the DEC Alpha implies that a is aligned on an 8-byte
boundary. Similarly, the predicate 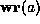 is true when the address a
denotes an aligned location that can be safely read or written. In essence,
these checks define what is meant by safety, and more specifically for this
example, memory safety. For the purpose of this paper, the predicates
is true when the address a
denotes an aligned location that can be safely read or written. In essence,
these checks define what is meant by safety, and more specifically for this
example, memory safety. For the purpose of this paper, the predicates
 and
and  are defined by the safety policy through the
precondition, as shown in the next subsection.
are defined by the safety policy through the
precondition, as shown in the next subsection.
 or
or  check fails. Instead, the execution blocks because there are no
transition rules covering the error cases. In this setting, a program is safe
if and only if it runs without blocking on the abstract machine. Of course, the
presence of these safety checks means that the abstract machine is not a
faithful abstraction of the DEC Alpha processor. However, the purpose of
certification is to prove that all safety checks always succeed. If we have a
valid safety proof for a program, we know that we can safely execute it on a
real DEC Alpha and get the same behavior as on our abstract machine, even
though the Alpha does not implement the safety checks.
check fails. Instead, the execution blocks because there are no
transition rules covering the error cases. In this setting, a program is safe
if and only if it runs without blocking on the abstract machine. Of course, the
presence of these safety checks means that the abstract machine is not a
faithful abstraction of the DEC Alpha processor. However, the purpose of
certification is to prove that all safety checks always succeed. If we have a
valid safety proof for a program, we know that we can safely execute it on a
real DEC Alpha and get the same behavior as on our abstract machine, even
though the Alpha does not implement the safety checks.
