



Next: The guarantee of safety
Up: Certifying the Safety of
Previous: Computing the safety predicate
We have intentionally written the program in ex-code in a slightly
complicated way, to show that low-level optimizations do not pose significant
problems in generating and validating safety proofs. Three of the
interesting properties of this program are (1) the instructions are somewhat
scheduled, including speculative execution of the load in line 2 and of the
addition in line 4, to accommodate the DEC Alpha pipeline
latency , (2) register
, (2) register 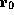 is reused in line 2
to hold the data word instead of the tag address, and (3) even though the
precondition is expressed as a function of the value in register
is reused in line 2
to hold the data word instead of the tag address, and (3) even though the
precondition is expressed as a function of the value in register 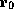 , some
of the actual memory accesses are done through register
, some
of the actual memory accesses are done through register 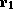 . In general,
we expect scheduling and register allocation to have no effect on the safety
predicate and its proof.
. In general,
we expect scheduling and register allocation to have no effect on the safety
predicate and its proof.

: A Fragment of the formal safety proof of 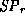 .
.
It is a simple exercise for the reader familiar with assembly-language
programming to verify that this code is indeed correct with respect to the
safety policy. The problem, of course, is how to convince even the most
suspicious kernel that this code is absolutely safe. To do this, we must prove
the safety predicate according to the rules of first-order predicate calculus
extended with two's-complement integer arithmetic. We refer to this set of
proof rules as  and we write
and we write 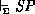 when the safety predicate
when the safety predicate
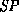 can be proved according to the rules in the set
can be proved according to the rules in the set 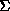 . Most of the
rules in
. Most of the
rules in 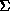 are simple. Below we show two of the rules we use, the first
being a classical implication-elimination rule from the predicate calculus, and
the second a rule about arithmetic:
are simple. Below we show two of the rules we use, the first
being a classical implication-elimination rule from the predicate calculus, and
the second a rule about arithmetic:
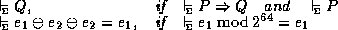
The second rule is perhaps a bit surprising because  is unconditionally true in integer arithmetic. However, for the machine
implementation of arithmetic, this statement is true only if the original
value of
is unconditionally true in integer arithmetic. However, for the machine
implementation of arithmetic, this statement is true only if the original
value of 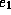 is a valid register value.
is a valid register value.
A large fragment of the proof of the safety predicate for our example program
is shown in a proof-tree form in ex-proof. This proof was
generated automatically by our system, which incorporates a simple theorem
prover. We use vertical dots to stand for extractions of a conjunct from the
precondition. You can read the proof tree from top to bottom, interpreting
every node as a valid inference of the predicate below the line using the
assumptions above the line. For example, in the upper-right corner of the
figure the predicate 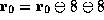 is proved using the arithmetic rule we
discussed with the assumption
is proved using the arithmetic rule we
discussed with the assumption 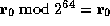 extracted from the
precondition. Then
extracted from the
precondition. Then 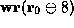 is proved using the implication-elimination
rule and the hypothesis u of the predicate
is proved using the implication-elimination
rule and the hypothesis u of the predicate 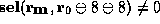 . This
hypothesis is introduced at a lower level in the proof tree, at the node
labeled u, for the purpose of proving the predicate
. This
hypothesis is introduced at a lower level in the proof tree, at the node
labeled u, for the purpose of proving the predicate 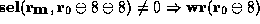 .
.



Next: The guarantee of safety
Up: Certifying the Safety of
Previous: Computing the safety predicate
Peter Lee
Tue Sep 17 15:37:44 EDT 1996
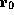 is reused in line 2
to hold the data word instead of the tag address, and (3) even though the
precondition is expressed as a function of the value in register
is reused in line 2
to hold the data word instead of the tag address, and (3) even though the
precondition is expressed as a function of the value in register 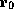 , some
of the actual memory accesses are done through register
, some
of the actual memory accesses are done through register 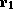 . In general,
we expect scheduling and register allocation to have no effect on the safety
predicate and its proof.
. In general,
we expect scheduling and register allocation to have no effect on the safety
predicate and its proof.


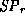 .
. and we write
and we write 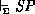 when the safety predicate
when the safety predicate
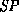 can be proved according to the rules in the set
can be proved according to the rules in the set 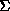 . Most of the
rules in
. Most of the
rules in 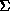 are simple. Below we show two of the rules we use, the first
being a classical implication-elimination rule from the predicate calculus, and
the second a rule about arithmetic:
are simple. Below we show two of the rules we use, the first
being a classical implication-elimination rule from the predicate calculus, and
the second a rule about arithmetic: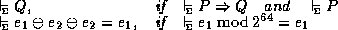
 is unconditionally true in integer arithmetic. However, for the machine
implementation of arithmetic, this statement is true only if the original
value of
is unconditionally true in integer arithmetic. However, for the machine
implementation of arithmetic, this statement is true only if the original
value of 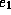 is a valid register value.
is a valid register value.
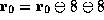 is proved using the arithmetic rule we
discussed with the assumption
is proved using the arithmetic rule we
discussed with the assumption 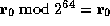 extracted from the
precondition. Then
extracted from the
precondition. Then 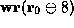 is proved using the implication-elimination
rule and the hypothesis u of the predicate
is proved using the implication-elimination
rule and the hypothesis u of the predicate 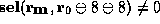 . This
hypothesis is introduced at a lower level in the proof tree, at the node
labeled u, for the purpose of proving the predicate
. This
hypothesis is introduced at a lower level in the proof tree, at the node
labeled u, for the purpose of proving the predicate 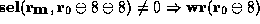 .
.