|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Security 2001 Paper
[Security '01 Tech Program Index]
Secure Distribution of Events in Content-Based Publish Subscribe SystemsElectrical Engineering and Computer Science Department University of Michigan Ann Arbor, MI 48109-2122 {lukasz,aprakash}@eecs.umich.edu AbstractContent-based publish-subscribe systems are an emerging paradigm for building a range of distributed applications. A specific problem in content-based systems is the secure distribution of events to clients subscribing to those events. In content-based systems, every event can potentially have a different set of interested subscribers. To provide confidentiality guarantee, we would like to encrypt messages so that only interested subscribers can read the message. In the worst case, for n clients, there can be 2n subgroups, and each event can go to a potentially different subgroup. A major problem is managing subgroup keys so that the number of encryptions required per event can be kept low. We first show the difficulties in applying existing group key management techniques to addressing the problem. We then propose and compare a number of approaches to reduce the number of encryptions and to increase message throughput. We present analytical analysis of described algorithms as well as simulation results.1 IntroductionMany of today's Internet applications require high scalability as well as strict security guarantees. This new breed of applications includes large wireless delivery services with thousands to millions of clients, inter-enterprise supply-chain management applications, financial applications, workflow applications, and network management.Messaging technology has been introduced to create much more flexible and scalable distributed systems. An emerging paradigm of messaging technology is publish-subscribe [B93]. In such systems, customers (or subscribers) specify the type of content they want to receive via subscriptions. Publishers publish messages (events), and the publish- subscribe system delivers them only to the interested subscribers. Publishers are often decoupled from subscribers, creating more scalable solutions. Figure 1 shows a typical publish-subscribe system. Events may be delivered via intermediate brokers, who determine the set of subscribers that an event should be delivered to. Decoupling of publishers and subscribers works well for increasing scalability but, as we will see, makes it difficult to develop secure solutions. The earliest publish-subscribe systems used subject-based subscription [B93, TIBCO]. In such systems, every message is labeled by the publisher as belonging to one of a fixed set of subjects (also known as groups, channels, or topics). Subscribers subscribe to all the messages within a particular subject or set of subjects. Strength of this approach is the potential to easily leverage group-based multicast techniques to provide scalability and performance, by assigning each subject to a multicast group. In fact, group communication can be considered to be a special case of subject-based subscription where the subject is the name of the group. A significant restriction with subject-based publish-subscribe is that the selectivity of subscriptions is limited to the predefined subjects. An emerging alternative to subject-based systems is content-based messaging systems [BCM99, C98, CDF, GKP99, KR95, MS97, SA97]. These systems support an event schema defining the type of information contained in each event (message). For example, applications interested in stock trades may use the event schema [issue: string, price: dollar, volume: integer]. A content-based subscription is a predicate against the event schema, such as (issue = "IBM" & price < 120 & volume > 1000). Only events that satisfy (match) the subscription predicate are delivered to the subscriber. With content-based subscription, subscribers have the added flexibility of choosing filtering criteria along multiple dimensions, without requiring pre- definition of subjects. In the stock trading example, a subject-based subscriber could be forced to select trades by issue name because those are the only subjects available. In contrast, a content-based subscriber is free to use any orthogonal criterion, such as volume, or indeed a predicate on any collection of criteria, such as issue, price, and volume. 
Fig. 1: An example of a publish-subscribe system. The applications listed above require different security guarantees. For example, an application distributing premium stock reports may require confidentiality to make sure that only authorized (paying) subscribers can access the data. Integrity may be required to ensure that reports have not been modified in transit from publishers to subscribers and sender authenticity to make sure that fake reports are not sent by third parties. The lack of those security guarantees in content-based systems has prevented their wider use even in applications that could greatly benefit from content-based subscriptions. The fact that in content-based systems every event can potentially go to a different subset of subscribers makes efficient implementation of confidentiality guarantees difficult. There are 2N possible subsets, where N is the number of subscribers. With thousands (tens of thousands or hundreds of thousands) of subscribers it is infeasible to setup static security groups for every possible subset. Even the use of a limited number of intermediate trusted servers/brokers to reduce the complexity can leave each broker with hundreds or thousands of subscribers, making the number of possible groups too large. This paper presents and compares several algorithms for secure delivery of events from a broker to its subscribers. Section 2 states the problem in detail. Section 3 presents related work. Section 4 explores a number of approaches based on the idea of using and caching multiple subgroup keys to address the secure end-point delivery problem. We described the use of these schemes and also present theoretical analysis of many of these approaches. Section 5 describes our simulation setup, experiment results and analysis of those results. Section 6 discusses the results and presents some theoretical bounds on the problem. Finally, Section 7 presents conclusions and directions for future work. 2 Problem DescriptionA messaging system routes events from a publisher to end-point brokers. The brokers then distribute those events to their subscribers. In content- based systems, each message could potentially go to a different set of subscribers (see Fig. 2). The picture shows two events (E1 and E2) delivered by the delivery system to the broker. Each event is then sent to a different subset of subscribers connected to the broker.We want to add certain security guarantees to content- based systems. The security requirement that we focus on in this paper is confidentiality. The system must guarantee that only authorized subscribers can read an event. Data must be protected from other (not authorized) subscribers as well as other malicious users on the network. 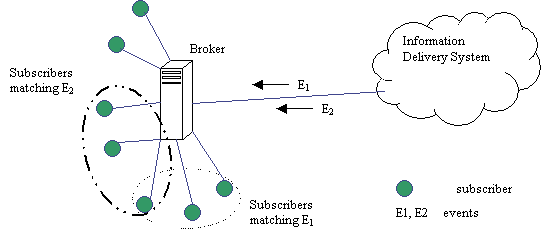
Fig. 2: Secure end-point delivery problem. This paper describes issues and solutions for only a subset of the complex security problem in an entire publish-subscribe system. To provide event confidentiality, we assume that events are protected on their way from a publisher, through the delivery system, to the end-point brokers. In this paper, we focus on the data security on the last leg from end-point brokers to subscribers in an efficient way when each broker may have a large number of clients. In this paper, we assume that all brokers are trusted and that all subscribers and publishers are properly authenticated to the system. All subscribers and publishers also have an individual symmetric pair-key shared only with their broker (generated during the authentication process). The issues of security in transit between publishers and end-point brokers as well as the issue of broker trust are the subjects of our future work. The publish-subscribe system allows dynamic access control to the events. This means that a predicate can be used at event publish time to check the set of subscribers who are authorized to receive the event. It is possible for a subscriber to be interested in an event (have a subscription for a particular event) but not be authorized to read that event (because of restrictions from a publisher). To simplify discussion, we assume that all interested subscribers are also authorized subscribers, i.e., each subscriber is authorized to read all events it subscribes to. Dynamic access control makes it infeasible to set up static security groups as each event can potentially have a different set of authorized subscribers (as well as a different set of interested subscribers). Given the above restrictions and assumptions, providing confidentiality in content-based systems in an efficient way is non-trivial. Since every event can potentially go to a different subset of subscribers, it is infeasible (for large numbers of clients) to set-up static security groups. The simplest solution would be to encrypt each event separately for every subscriber receiving the event (using individual subscriber keys). For large systems where each broker has thousands of subscribers, this could mean hundreds or thousands of encryptions per event. An additional performance hit involves changing keys for each of the encryptions, which drastically slows down encryption algorithms like DES [Pub97]. We tested this by encrypting a random 64-bit piece of data with DES. We compared throughput when continuously encrypting with one key and when using 500 different keys on a Pentium III 550 Mhz machine running Red Hat Linux. The results showed that changing keys for each subscription results in throughput as low as 10% of the total throughput when using only one key. In short, the problem presented here is to preserve confidentiality using small number of encryptions while distributing events from end-point broker to its subscribers. Due to lack of good workloads in this area, we consider two extreme scenarios --- (1) where events go to random subgroups of subscribers and (2) where there are some popular subgroups and some unpopular subgroups. The simplest solution is to encrypt each event separately for every subscriber receiving the event. This solution does not scale to large, high volume systems due to the throughput reduction of encryption algorithms like DES. This paper explores a number of dynamic caching approaches to reduce the number of encryptions and to increase message throughput. 3 Related WorkUntil this point, the problem of efficiently delivering events in a confidential manner to only interested subscribers has not been addressed in content-based systems. However, a related and active area of research is secure group communication. Specifically, group key management services are closely related to the problem described above. Secure group communication systems are usually meant to provide secure channel for the exchange of data between group members. Secure groups are often identified by a session key, known to all group members, which is used to encrypt all data sent to the group. Key management services are used to facilitate member joins and leaves (including expulsions) as well as periodic re-keying to ensure validity of the session key.A related area of work is research on broadcast encryption. It was first introduced by Fiat and Naor [FN93] in the context of pay-TV. The authors presented methods for securely broadcasting information such that only a selected subset of users can decrypt the information while coalitions of up to k unprivileged users learn nothing. Unfortunately, schemes presented in [FN93] as well as in extensions found in [BC94, BFMS98, SvT98] require a large numbers of keys to be stored at the receivers or large broadcast messages. Another problem in the context of secure content-based systems is that coalition of more than k unprivileged users can decrypt the information. Luby and Staddon [LS98] studied the trade-off between the number of keys stored in the receivers and the transmission length in large and small target receiver sets. They prove a lower bound that shows that either the transmission must be very long or a prohibitive number of keys must be stored in the receivers. An extension proposed in [ASW00] decreases the number of keys required and the length of transmissions by relaxing the target set. It allows a small fraction of users outside the target set to be able to decrypt the information. Such scheme may work well for pay-TV and similar applications but is unacceptable when confidentiality of broadcast information must be preserved. The problem of secure event delivery from end-point brokers to subscribers can be cast as group communication with very dynamic membership. Since in content-based systems each event goes to a potentially different and arbitrary subset of subscribers, it is likely that two events arriving one after another go to completely different subsets of subscribers. If a group communication system were used to distribute events from a broker to subscribers, a group would have to be reconstructed (possibly entirely) for every event arriving at the broker. We describe a number of group key management approaches and show that none of the existing algorithms was designed to support dynamic membership changes that occur in content-based systems. The key management techniques for group communication are likely to have a large overhead when used in content-based system context. A simple group key distribution method would be to create a pair-key between each subscriber and its broker. Whenever there is a membership change, the new session key is distributed to each member using its pair key. If an event requires a new subgroup of size N, this requires N encryptions to send a new session key. Since membership in content-based systems can potentially change for every event, this cost can be high for large groups. One of the first attempts at standardizing secure multicast, GKMP [HM97a][HM97b] defines a protocol under which group session keys can be efficiently distributed. In GKMP, after being accepted into the group, newly joined members receive a Key Encrypting Key (KEK) under which all subsequent session keys are delivered. A limitation of this approach is that that there is no backward or forward secrecy. Anyone with the possession of the KEK can potentially access all the past and future session keys. The only way in GKMP to provide backward and forward secrecy is to reform the group with a new KEK. Obviously, the GKMP protocol does not support confidentiality requirements of content-based systems where events need to be protected from all but interested subscribers for that specific event. Mittra's Iolus system [M97] attempts to overcome the problems in scalability of key distribution by introducing locally maintained subgroups. Each subgroup maintains its own session key, which is modified on membership events. Subgroups are arranged in a tree hierarchy. This solution is more scalable than the simple group key distribution method for membership changes. And, in fact, our approach of assigning subscribers to brokers is similar to the approach of subgrouping in Iolus. However, in the worst case, note that the session keys for all the subgroups may need to be changed for each event. And changing the key in a subgroup could potentially require linear number of encryptions in the number of subscribers within each subgroup. The cost of changing keys in Iolus within subgroups can be reduced by making smaller subgroups. In the extreme case, for example, a small fixed number, K, of subscribers can be assigned to each subgroup, irrespective of the total number of subscribers, N. In that case, however, one ends up with a large number of intermediate servers (N/K) who must be trusted with the content of all the events sent via the system. We would like to explore solutions that reduce the number of servers we trust with event contents to as low values as feasible. Approaches based on logical key hierarchies [WHA98][WGL98][YL00] provide an efficient approach to achieving scalable, secure key distribution on membership changes in group communication systems. A logical key hierarchy (LKH) is singly rooted d-ary tree of cryptographic keys (where d is usually 2, but can be arbitrary). A trusted session leader assigns the interior node keys, and each leaf node key is a secret key shared between the session leader and a single member. Once the group has been established, each member knows all the keys along the path from their leaf node key and the root. As changes in membership occur, re-keying is performed by replacing only those keys known (required) by the leaving (joining) member. It can be shown that the total cost of re-keying in key hierarchies in response to a single join or leave scales logarithmically with group size [WHA98][WGL98]. If the change in membership from the initial tree is O(N), as is the case with a random group change, it may require up to O(N log(N)) number of encryptions if members are removed (or added) individually. We consider that too high. If the tree is entirely reconstituted for each event being sent to a subgroup of size k, the number of encryptions required per event is at least k, which can still be large. Another approach based on LKH uses the intermediate keys of the full tree. Instead of rebuilding the tree to represent the appropriate subgroup for each event, the tree can be searched to find the smallest subset of intermediate keys that cover all subscribers interested in the particular event. The search process is O(N) but the number of encryptions can be much smaller than in the tree rebuilding case. We compare our algorithms to this scheme in Section 5. The VersaKey system [WCS99] extends the LKH algorithm by converting the key hierarchy into a table of keys, based on binary digits in the identifiers of the members. In this scheme, in the case of joins, no key distribution to current members is necessary. However, the VersaKey approach is vulnerable to collusion of ejected members. For example, two colluding members with complimentary identifiers cannot be ejected without simultaneously replacing the entire table. It is likely therefore that the table would need to be replaced for a large percentage of events going through the end-point broker. A number of key agreement protocols (as opposed to key distribution approaches outlined above) have been suggested in which group keys are created from contributions of inputs (or key shares) of desired members [ITW82, SSD88, BD94, BW98, STW00, KPT00]. The general approach taken in these protocols is to extend the 2-party Diffie-Helman exchange protocol to N parties. Due to the contributory nature and perfect key independence, most of these protocols require exponentiations linear in the number of members [Steiner 2000] for most group updates. Kim et al unify the notion from key hierarchies and Diffie- Helman key exchange to achieve a cost of O(log(N)) exponentiations for individual joins; however, the number of exponentiations for k joins or leaves will still be usually at least linear in k (unless the nodes that are leaving happen to be all clustered in the same parts of the key tree). Since exponentiation is expensive, these protocols are primarily suitable for establishing small groups at present and not suitable when group membership can change drastically from event to event. We thus exclude them for further consideration in this paper, and instead focus on approaches based on key distribution protocols. Since the secure end-point delivery problem is only a part of a larger publish-subscribe system, we briefly describe related publish subscribe systems as well. Relatively few event distribution systems [W98] allow subscriptions to be expressed as predicates over the entire message content. A few noteworthy examples of this emerging category are SIENA [C98], READY [GKP99], Elvin [SA97], JEDI [CDF], Yeast [KR95], GEM [MS97], and Gryphon [BCM99]. All of these systems support rich subscription predicates, and thus face problems of scalability in their event distribution algorithms. None of the above systems offers any security features. Other, traditionally subject-based, publish- subscribe systems are also moving towards richer subscription languages. The Java Message Service (JMS) [SUN] enables the use of message selectors, which are predicates over a set of message properties. The OMG Notification Service [OMG] describes structured events with a "filterable body" portion. The TIB/Rendezvous system [TIBCO] available from the TIBCO Corporation has a hierarchy of subjects and permits subscription patterns over the resulting segmented subject field, also approximating some of the richness available with content-based subscription. A new version of the Elvin system, Elvin 4 [SAB00], introduces a notion of keys for security [ABH00]; the details available are sketchy but it appears that the correct use and distribution of keys is up to the clients and servers, rather than being automatically managed by the underlying infrastructure based on subscriptions and event contents. 4 Group Key CachingOur main goal is to reduce the number of encryptions required to ensure confidentiality when sending events from end-point brokers to subscribers. This reduction in number of encryptions in turn increases event throughput necessary for large and scalable systems. Due to the complexity of the problem – there are 2N possible subgroups (where N is the number of subscribers) and every event can potentially go to a different subgroup – this paper explores only dynamic caching algorithms.Our algorithms are compared to the naïve solution (described below) and the number of encryptions required by the naïve solution is our upper bound. Our algorithms must use less encryptions than the naïve algorithm without introducing other performance overheads. The naïve approach is described in figure 3:  For every event arriving at an end-point broker and matching to K subscribers, the naïve approach needs K encryptions. For a broker with N subscribers, and a random distribution of groups (sets of subscribers interested in an event), an average event goes to N/2 subscribers. This means that with 1000 subscribers per broker, a broker must on average perform 500 encryptions per event. Our approaches aim to improve on that number. All of our dynamic caching algorithms require the broker and subscriber to keep a certain size cache. In general, the cache stores keys for most popular groups. Cache entries have the following format: < G, KG > G is a bit vector identifying which subscribers belong to the group and KG is the key associated with the group. KG is used to encrypt events going to this particular set of subscribers. We assume that all subscribers have enough resources to cache all necessary keys. Subscriber S1 must cache every entry < GX, KX > cached at the broker such that S1 belongs to G. In practice, subscribers with limited resources may have smaller caches. This means that such subscriber may not have all the appropriate keys cached at the broker. A secure protocol for key request/exchange has to be developed to in order for our caching algorithms to support subscribers with limited resources. Currently, we assume every subscriber has all the cache entries {< G, K > | S belongs to G} cached at the broker. The next few sections describe each of our algorithms in detail. We present theoretical analysis and simulation results comparing each of our approaches and the naïve solution. We also present simulation results for LKH-based solution for comparison. We derive approximate expressions for the average number of encryptions for two different distributions of groups: Random – each arriving event goes to a random subset of subscribers. Every one of the possible 2N groups has the same probability of occurrence. Popular Set – there is a set of groups that happen more often
than others. An event has a higher probability of matching a group from
the popular group set S. The distribution has the following parameters:
|S|: the size of set S (number of groups in the popular set) p: probability that an event matches a group from S Every event matches a random group from S with probability p. Every event matches a totally random group with probability (p – 1).
We introduce a measure of average number of encryptions per message E. Due to uniform distribution of subscribers in a group, the average number of subscribers in a group is N/2, so:
4.1 Simple CachingThe simplest solution to reducing the number of encryptions in the system is to use a plain caching scheme. This approach assumes that, based on customer subscriptions, many events will go to the same subset of subscribers. Creating and caching a separate key for those groups would take advantage of repeating groups and it would reduce the number of encryptions performed at the broker. The major parameters affecting the performance of this approach are the number of clients, cache size, and the distribution of groups. The basic algorithm works as follows:
2.1 if an entry < G, KG > is found in cache and send it to the set of subscribers G Random distribution: we know that if there is a cache hit (incoming event matches a group stored in cache), the event only needs to be encrypted once with the stored key. If there is a cache miss, then the number of encryptions is the same as in the naïve case. The probability of a cache hit is: Where C is the cache size and N is the number of subscribers. The probability of a cache miss is: From equations 2a and 2b we can get the expression for the average number of encryptions per message: We can see that as the number of subscribers gets larger, the simple cache will perform only slightly better than the naïve approach. For 100 subscribers and a cache of size 10,000, this approach averages 50 encryptions per message (just like the naïve solution). Popular-set distribution: there are 2 cases: whether the group comes from the popular set or not (since the smart cache only caches groups from the popular set). If the group does not come from the popular set (with probability (1-p)) then the average number of encryptions is: If the group comes from the popular set, then the number of encryptions depends on whether there was a cache hit or not. Similarly to the simple cache with random groups, the average number of encryptions for groups coming from the popular set is: Combining equations 4a and 4b, we get the expression for average number of encryptions with simple cache and popular set distribution: For the same parameters as in the random distribution case and the popular set of size 10,000 and probability p = .9, simple cache requires only 6 encryptions on average.
4.2 Build-up CacheThis algorithm extends the simple caching approach. The base of this solution is an observation that many groups are subsets of other, larger groups. In other words, larger groups can often be constructed by combining smaller groups. The algorithm takes advantage of this observation by performing partial cache matching. It searches for subsets of a given group G trying to reconstruct G using a number of smaller groups already in the cache. Figure 4 shows the basic idea behind the algorithm. Optimally, the algorithm would try to find a minimum number of groups from cache that completely cover group G. This would make the algorithm intractable. We use a heuristic that reduces the complexity of the search process to O(C), where C is the size of the cache. We search the cache from largest to smallest entries based on the assumption that finding a larger matching group will lead to a better overall match. The details are as follows:
2.1. if a full match is found (entry < G, KG > is found in cache) 4.3 Clustered CacheA known technique for reducing complexity of certain problems is clustering [reference]. There are 2N possible groups and the above approaches may require very large cache sizes when the number of subscribers grows into thousands. This section describes a new clustered cache technique, which needs much smaller number of encryptions than the first two algorithms.For a server with N clients, we divide the set of clients into K clusters.
The server has to keep K separate cluster caches, but those caches
can be much smaller than the caches from section 4.1 and 4.2. Each cluster
cache holds entries of the same format as the simple and buildup caches
(< G, KG >), but G only consists of subscribers belonging
to the particular cluster. The algorithm works in the following way:
3.1. search cluster cache for the appropriate group (one of G1 through GK) An interesting issue in this algorithm is the choice of clusters. A simple solution is to assign subscribers to clusters randomly (or according to subscriber ids: first X subscribers to cluster 1, next X to cluster 2, etc.). Another approach would be to assign clusters based on subscription similarity. Subscribers with similar subscriptions would be assigned to the same cluster. We calculate the average number of encryptions per each cluster and multiply it by the number of clusters to get the total. A cluster of size NK, with individual cache of size Ck is very much like the simple cache from previous section. We present approximate formulas for random distribution only. Derived from equation 2, the average number of encryptions per cluster is: The average number of encryptions for clustered cache is Ek * K, so:
Next section describes an algorithm combining clustered and simple caches
that combines the advantages of both approaches.
4.4 Clustered-Popular CacheThe clustered cache works well in a generic case of random groups. It doesn't take advantage of the fact that some groups occur more frequently, as in the popular-set distribution. The clustered-popular algorithm was designed to enhance clustered cache with support for frequently occurring (popular) groups. The basic idea is to combine clustered cache with simple cache in one. For each event, both caches are checked. If there is no hit in the simple part of the cache, the clustered approach is used to reduce the number of encryptions. The algorithm works as follows:
2.1. if an entry < G, KG > is found in cache
Random distribution: if there is hit in the simple part of the cache, we need only 1 encryption. Otherwise, the number of encryptions is the same as in the clustered cache. Here, C is the size of the simple part of the cache and CK is the size of clusters in the clustered part of the cache. We assume the following two conditions: With those conditions, the approximate formulas for the average number of encryptions are shown in figure 5, equation 5. Popular distribution: We know that if the group does not come from the popular set (probability (1 – p)), there is no hit in the simple part of the cache (smart cache and we assume that C < |S|). In this case, the average number of encryptions is based only on the clustered part of the cache (figure 5, equation 6a). If the group comes from the popular set then there is a hit in the simple cache with probability In case of simple cache miss, clustered cache is checked with probability The average number of encryptions when a group comes form the popular set S is shown in figure 5, equation 6d. Combination of equations 6a and 6d gives us a formula for the average number of encryptions for the clustered-popular cache and popular-set group distribution (figure 5, equation 6). Table 1 shows average numbers of encryptions calculated using formulas derived above for two different sets of parameters. The clustered-popular approach always uses half of the cache for the simple part and second half for the clustered part. The small set has the following parameters: there are 100 clients and cache size is 10,000 entries. The clustered approach uses 10 clusters of 10 subscribers each with cluster cache size of 1000. The clustered-popular cache uses 11 clusters of about 9 subscribers each. The popular set distribution uses a set of 10,000 groups and probability p = .9. The large set has the following parameters: there are 1,000 clients and cache size is 100,000 entries. The clustered cache uses 100 clusters of 10 subscribers. The clustered-popular cache uses 114 clusters of 8 or 9 subscribers each. The popular set has 100,000 groups and probability p = .8.
Clustered-popular cache performs best in the large set and the popular-set group distribution. Next section shows that the clustered-popular approach outperforms other algorithms as the size of the cache increases. The actual numbers for both clustered algorithms should be lower than the theoretical values. This is because we did not account for the fact that for some events, not all clusters will have interested subscribers. This was done to simplify derivation. Also, the values for simple cache should be higher because of our assumption of smart cache. We were not able to approach the smart cache because of the size of our sample in the simulations. 5 SimulationsWe ran a number of simulations to confirm our theoretical results as well as to compare the simple, clustered, and clustered-popular approaches to the build-up cache as well as to an LKH-based approach presented for comparison. The LKH based approach works by creating a hierarchical tree of keys. When an event arrives at broker and is matched to a group of subscribers G, the tree is searched, bottom-up, for keys that are common to as many as possible subscribers from G but are not know to subscribers not in G. The LKH-based scheme corresponds to a fixed cache size – the key tree only changes with changes in the number of subscribers. We ran a number of simulations testing different parameter settings. Each simulation consisted of 15,000 events. All caches were warm. We show results for both, random and popular-set, group distributions. The number of clusters used by the cluster-based algorithms depends on the number of clients. When solving equation 4 for the number of clusters K, we get the optimal number of clusters when (NK is the number
of clients per clusters and CK is the cluster cache size). We
chose the largest K which gave (NK is the number
of clients per clusters and CK is the cluster cache size). We
chose the largest K which gave 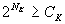 . We used
the same method to determine number of clusters for the clustered popular
approach. . We used
the same method to determine number of clusters for the clustered popular
approach.
Figure 6 shows results for cache size 10,000, and figure 7 shows results for cache size 20,000. Figure 7 shows results for only the clustered, clustered- popular, and LKH-based approaches.
The clustered-popular is the only algorithm that performs differently with popular-set group distribution. We can see that clustered, clustered- popular, and LKH-based algorithms outperform the simple and build-up caches for random groups. In the case of popular-set distribution, all perform similarly with LKH-based approach being the worst. When the cache size is increased to 20,000, the clustered approaches clearly outperform the LKH-based algorithm. Figure 8 shows the effect of increasing cache size on the number of encryptions required by each algorithm for different group distributions. The results (except for the LKH-based approach, which is based on simulation results) in this figure are based on the approximate formulas derived in section 4. As we can see, clustered and clustered-popular approaches are similar with random group distribution, but the clustered-popular algorithm clearly outperforms all other solutions when the popular-set distribution is used. In order to make judgments about usefulness of any of these algorithms, we need to relate number of encryptions to a performance measure like throughput.
We claimed that algorithms that reduce the number of encryptions required are desirable because large number of encryptions per message reduces message throughput at the broker. We measured throughput of the DES algorithm depending on the number of encryptions per message to show that this is the case. We ran a number of experiments encrypting an 8-byte piece of data. We varied the number of different keys used. We used the DES algorithm on a 550Mhz Pentium III running RedHat Linux operating system.
The results of our experiment are showed in fig. 9. The adverse effect of number of encryptions on throughput is clearly visible. Based on our results, we see that clustered-popular has higher throughput than LKH-based approach by approximately 100% in the case of popular-set distribution and by about 33% in the case of random group distribution. Clustered-popular is also about 50% better than clustered algorithm for popular-set distribution, it, however, underperforms clustered algorithm by about 10-20% in the case of random distribution. The LKH-based approach also has approximately 40% lower throughput than the clustered algorithms. 6 DiscussionWe can draw the following conclusions from the above results:
The reduction over simple caching and LKH that we considered appears to be asymptotically a constant factor for the same size cache. A question that arises is whether it is possible to do reduce the number of encryptions to O(log N) per event in the worst case, by either using multiple static LKH trees or by using a large cache. The answer appears to be no as the following analysis shows unless the cache size is exponential in the number of clients. Since the internal nodes of an LKH tree can also be considered to be cache entries, the result also says that an exponential number of LKH trees are required to reduce the worst-case bound on the number of encryptions to be O(log(N)) per event. In the analysis below, we only consider the situation where generating a group key for a new event uses an optimal combination of existing keys in the cache. Suppose the cache size is S. If we are allowed to pick at most p entries from the cache to form any subgroup, the maximum number of subgroups that can be formed from this cache is bounded by: But, there are 2N subgroups that need to be formed, given N clients. Therefore, if each potential subgroup needs to be formed using at most p cache entries, the following must hold: Therefore, Or The above result tells us that if p is any sublinear function of N (e.g., O(ln N) or O(sqrt(N))), the size of the cache must grow exponentially in N to guarantee that each event can be sent securely using at most p encryptions. So, it appears that the worst-case number of encryptions for an event will need to be linear in N for reasonably sized caches, but one can try to improve the constant of proportionality, as we have tried to do in this paper. Note that this result applies only if a new event needs to be encrypted individually using existing (potentially multiple) group keys. An open question is whether one can do better if one allows an event to be encrypted multiple times; e.g., send a message encrypted under both keys k1 and k2, to send the message to only those members who possess both k1 and k2. Another open question is whether sublinear amortized bounds can be achieved without exponential- size caches. We leave the analysis of these questions to future work. 7 Conclusion and Future WorkThere is a growing need for security solutions for content-based systems. This paper identifies the "secure end-point delivery" problem and explores a number of possible solutions. We are concerned with providing confidentiality when sending events from brokers to subscribers. The problem is that in content-based systems, every event can potentially have a different set of interested subscribers. There are 2N possible subsets, where N is the number of subscribers. With thousands of subscribers it is infeasible to setup static security groups for every possible subset.A number of key management systems for group communication solve a similar problem but none of them was designed to handle the dynamic nature of content-based event delivery. We explored a number of dynamic caching approaches. A simple solution is to encrypt each event separately for each interested subscriber; however this requires a large number of encryptions for large sets of subscribers. Our main goal is to reduce the number of encryptions required to preserve confidentiality while sending events only to interested subscribers. The number of encryptions is important because it translates directly into message throughput (see figure 9). All of our approaches use a dynamic caching scheme, where the broker and subscribers must cache subgroup keys. Each cache entry has a format < G, K >, where G identifies the set of subscribers belonging to a subgroup and K is a key associated with the subgroup. All secure communication intended for all subscribers in G can be encrypted using key K. Through theoretical analysis and simulation results, we show that our clustered and clustered-popular approaches perform better as cache size increases. Both cluster-based algorithms outperform LKH-based solution for most cases. Clustered-popular algorithm performs especially well in the case of the popular-set group distribution. We also show that it is impossible to achieve sublinear encryptions growth for a large class of algorithms, even with using multiple LKH trees, without an exponential number of LKH trees or exponential-sized caches in the number of subscribers per broker. Our results show that cluster-based algorithms can be a practical solution
to the end-point delivery problem. They do not impose heavy overhead as
hash tables can be used for cache lookup. The cache size requirement on
the subscriber side is also lower than the simple cache or build-up cache
algorithms. In the case of the clustered cache, each subscriber only needs
Ck cache entries, where We plan to investigate the effect of providing integrity and sender authentication on message throughput in the future. Efficient sender authentication in the context of content-based systems is a non-trivial problem. Throughout the paper we make an assumption that brokers are trusted. Every broker in the system has the ability to read every event. We are investigating the impact of non-universal broker trust on the design of algorithms. References[ABH00] D. Arnold, J. Boot, M. Henderson, T. Phelps, and B. Segall. Elvin – Content- Addressed Messaging Client Protocol. Internet Draft, Network Working Group, 2000. Available from http://elvin.dstc.edu.au/download/internet-draft.txt.[ASW00] M. Abdalla, Y. Shavitt, and A. Wool. Key Management for Restricted Multicast Using Broadcast Encryption. IEEE/ACM Transactions on Networking, 8(4), pp 443- 454, August 2000. [B93] K. Birman. The Process Group Approach to Reliable Distributed Computing. Communications of the ACM, 36(12):37 53, December 1993. [B96] A. Ballardie. Scalable Multicast Key Distribution. Internet Engineering Task Force, May 1996. RFC 1949. [BC94] C. Blundo and A. Cresti. Space requirements for broadcast encryption. In Advances in Cryptology – EUROCRYPT'94, LNCS 950, pp 287-298. Springer-Verlag, 1994. [BCM99] Guruduth Banavar, Tushar Chandra, Bodhi Mukherjee, Jay Nagarajarao, Robert E. Strom, and Daniel C. Sturman. An Efficient Multicast Protocol for Content- Based Publish-Subscribe Systems. In International Conference on Distributed Computing Systems (ICDCS '99), June 1999. [BD94] M. Burmester and Y. Desmedt. A secure and efficient conference key distribution system. In Advances in Cryptology – EUROCRYPT '94, 1995. [BFMS98] C. Blundo, L. A. Frota Mattos, and D. R. Stinson. Generalized Beimel-Chor schemes for broadcast encryption and interactive key distribution. In Theoretical Computer Science, 200(1-2), pp 313-334, 1998. [BW98] K. Becker and U. Wille. Communication complexity of group key distribution. In 5th ACM Conference on Computer and Communications Security, San Francisco, CA, November 1998. [C98] Antonio Carzaniga. Architectures for an Event Notification Service Scalable to Wide-Area Networks. PhD thesis, Politecnico di Milano, December 1998. Available: http://www.cs.colorado.edu/ ~carzanig/papers. [CDF] G. Cugola, E. DiNitto, and A. Fuggetta. The JEDI event-based infrastructure and its application to the development of the OPSS WFMS. Submitted to Transactions on Software Engineering [CDZ97] K. Calvert, M. Doar, and E. Zegura. Modeling Internet Topology. IEEE Communications Magazine, June, 1997. [D89] S. Deering. Host Extensions for IP Multicasting. IETF RFC 1112, August 1989. [GKP99] R. Gruber, B. Krishnamurthy, and E. Panagos. An Architecture of the READY Event Notification System. In Proceedings of the Middleware Workshop at the International Conference on Distributed Computing Systems 1999, Austin, TX, June 1999. [HH99] Hugh Harney and Eric Harder. Group Secure Association Key Management Protocol (Draft). Internet Engineering Task Force, April 1999. draft-harney-sparta- gsakmp-sec-00.txt. [HM97a] H. Harney and C. Muckenhirn. Group Key Management Protocol (GKMP) Architecture. Internet Engineering Task Force, July 1997. RFC 2094. [HM97b] H. Harney and C. Muckenhirn. Group Key Management Protocol (GKMP) Specification. Internet Engineering Task Force, July 1997. RFC 2093. [ITW82] I. Ingemarsson, D. Tang, and C. Wong. A conference key distribution system. IEEE Transactions on Information Theory, vol. 28, no. 5, pp. 714-720, September 1982. [IONA] IONA Corporation. OrbixTalk Fact Sheet. http://www.iona.com/products/messaging/t alk/index.html. [KPT00] Y. Kim, A. Perrig, and G. Tsudik. Simple and Fault-Tolerant Key Agreement for Dynamic Collaborative Groups. In Proceedings of 7th ACM Conference on Computer and Communication Security CCS 2000. [KR95] B. Krishnamurthy and D. Rosenblum. Yeast: A general purpose event-action system. IEEE Transactions on Software Engineering, 21(10), October 1995. [LS98] M. Luby and J. Staddon. Combinatorial bounds for broadcast encryption. In Advances in Cryptology – EUROCRYPT'98, LNCS 1403, pp 512-526, Espoo, Finland, 1998. [M97] S. Mittra. Iolus: A Framework for Scalable Secure Multicasting. In Proceedings of ACM SIGCOMM '97, pages 277 - 278. ACM, September 1997. [MPH99] P. McDaniel, A. Prakash, and P. Honeyman. Antigone: A Flexible Framework for Secure Group Communication. In Proceedings of the 8th USENIX Security Symposium, August 1999. [MS97] M. Mansouri-Samani and M. Sloman. A Generalised Event Monitoring Language for Distributed Systems. EE/IOP/BCS Distributed Systems Engineering Journal, 4(2), June 1997. [MS98] David A. McGrew and Alan T. Sherman. Key Establishment in Large Dynamic Groups Using One-Way Function Trees. TIS Report No. 0755, TIS Labs at Network Associates, Inc., Glenwood, MD, May 1998. [OAA00] L. Opyrchal, M. Astley, J. Auerbach, G. Banavar, R. Strom, and D. Sturman. Exploiting IP Multicast in Content-Based Publish-Subscribe Systems. In Proceedings of Middleware 2000, New York, April 2000. [OMG] Object Management Group. Notification Service. http://www.omg.org/cgi-bin/ doc?telecom/98-06-15 [P99] Adrian Perrig. Efficient Collaborative Key Management Protocols for Secure Autonomous Group Communication. In International Workshop on Cryptographic Techniques and E-Commerce (CrypTEC '99), 1999. [Pub77] Federal Information Processing Standards Publication. Data Encryption Standard, 1997. National Bureau of Standards. [R94] M. Reiter. Secure Agreement Protocols: Reliable and Atomic Group Multicast in Rampart. In Proceedings of 2nd ACM Conference on Computer and Communications Security, pages 68 - 80. ACM, November 1994. [SA97] Bill Segall and David Arnold. Elvin has left the building: A publish/subscribe notification service with quenching. In Proceedings of AUUG97, Brisbane, Australia, September 1997. [SAB00] B. Segall, D. Arnold, J. Boot, M. Henderson, and T. Phelps. Content Based Routing with Elvin4. To appear in Proceedings AUUG2K, Canberra, Australia, June 2000. [SSD88] D. Steer, L. Strawczynski, W. Diffie, and M. Wiener. A secure audio teleconference system. In Advances in Cryptology – CRYPTO '88, Santa Barbara, CA, August 1998. [SvT98] D. R. Stinson and T. van Trung. Some new results on key distribution patterns and broadcast encryption. Designs, Codes and Cryptography, 14(3), pp261-279, 1998. [STW00] M. Steiner, G. Tsudik, and M. Waidner. Key Agreement in Dynamic Peer Groups. IEEE Transactions on Parallel and Distributed Systems, 2000. [SUN] Sun Microsystems. Java Message Service. http://java.sun.com/products/jms. [TIBCO] TIBCO. TIB/Rendezvous White Paper. http://www.rv.tibco.com/whitepaper.html. [VBM96] R. Van Renesse, K. Birman, and S. Maffeis. Horus: A Flexible Group Communication System. Communications of the ACM, 39(4):76 - 83, April 1996. [WGL98] C. K. Wong, M. Gouda, and S. S. Lam. Secure Group Communication Using Key Graphs. In Proceedings of ACM SIGCOMM '98, pages 68 - 79. ACM, September 1998. [WHA98] Debby M. Wallner, Eric J. Harder, and Ryan C. Agee. Key Management for Multicast: Issues and Architectures (Draft). Internet Engineering Task Force, September 1998. draft-wallner-key-arch- 01.txt. [WISEN98] Workshop on Internet Scale Event Notification. See http://www.ics.uci.edu/ IRUS/wisen/wisen98 for details. [WCS99] M. Waldvogel, G. Caronni, D. Sun, N. Weiler, and B. Plattner. The VersaKey Framework: Versatile Group Key Management. IEEE Journal on Selected Areas in Communications, 17(9), September 1999. [YL00] Y. Yang and S. Lam. A Secure Key Management Protocol Communication Lower Bound. Technical Report TR2000- 24, The University of Texas at Austin, Austin, TX, September 2000. [ZCB96] E. Zegura, K. Calvert, and S. Bhattacharjee. How to Model an Internetwork. In Proceedings of IEEE Infocom `96, San Francisco, CA, April 1996. This work is supported in part by the IBM Research Partnership Award and by the Defense Advanced Research Projects Agency (DARPA) and Air Force Research Laboratory, Air Force Materiel Command, USAF, under agreement number F30602-00-2-0508. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright annotation thereon. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of DARPA, the Air Force Research Laboratory, or the U.S. Government. |
|
This paper was originally published in the
Proceedings of the 10th USENIX Security Symposium,
August 13–17, 2001, Washington, D.C., USA
Last changed: 2 Jan. 2002 ml |
|