|
USENIX Technical Program - Paper - Smartcard 99
[Technical Program]
Efficient Block Ciphers for Smartcards
Joan Daemen
Proton World Int'l
Zweefvliegtuigstraat 10
B-1130 Brussel, Belgium
daemen.j@protonworld.com
Vincent Rijmen1
K.U.Leuven, Dept. ESAT
Kard. Mercierlaan 94
B-3001 Heverlee, Belgium
vincent.rijmen@esat.kuleuven.ac.be
Abstract
We present a family of block ciphers that can be implemented very efficiently
on cheap Smartcard processors. The ciphers use a very small amount of RAM and
a reasonable amount of ROM. Both cipher execution and key setup/key change are
very fast. The ciphers resist theoretical and practical cryptanalytic attacks
and in their design timing and power analysis attacks have been taken into
account.
1 Introduction
In many applications Smartcards are used as portable secure devices. For their security the applications make use of MAC generation/verification and encryption/decryption using a block cipher. We present a family of block ciphers that are suited for this purpose. Additionally, all these ciphers can be used as efficient one-way function and the variants with block size of 196 bits or higher are efficient compression function to form an iterated cryptographic hash function. The family is named after its first member that was designed and published: Square [1].
Currently, the Square family consists of three ciphers: Square, with a block length and a key length of 128 bits; BKSQ with a block length of 96 bits and a variable key length (96, 144 or 192
bits); and Rijndael with a variable block length and key length (both can be independently
specified at 128, 192 or 256 bits). The three ciphers are designed to be secure against all known cryptographic attacks. For a treatment of cryptographic security and the design rationale we refer to [1,2,3]. This paper treats implementation aspects and in particular those specific for Smartcards.
In Section 2 we present the common cipher structure of the
Square family. Section 3 discusses the implementation of the
ciphers on typical Smartcard processors. Section 4 treats the features
of the presented ciphers to thwart attacks that exploit typical weaknesses of
cipher implementations on Smartcards. Section 5 lists concrete
performance figures.
2 Cipher structure
A Square cipher is an iterated block cipher: it consists of the repeated application of a round transformation that is parameterized by a round key. The round keys are derived from the cipher key by means of a key schedule. The block length is indicated by n, the cipher key length by m and the number of rounds by r.
2.1 The round transformation
The round transformation is composed of four invertible uniform transformations, called steps. These steps can be described most easily by thinking of the input as a rectangular byte array. The dimensions of this byte array vary for the different members of the family, and depend on the block size.
The four steps are described as follows (cf. Figure 1).
- The diffusion step:
- Every byte is replaced by a linear combination of
the bytes within the same column. The bytes are considered as elements in
the field GF(28).
- The dispersion step:
- A permutation of the bytes over different columns.
This is done by shifting the rows of the byte array over different amounts,
or by a transposition of the byte array (for Square).
- The nonlinear step:
- A substitution of the bytes by means of a nonlinear
lookup table.
- The round key addition:
- The bytes are EXORed with an n-bit round key.
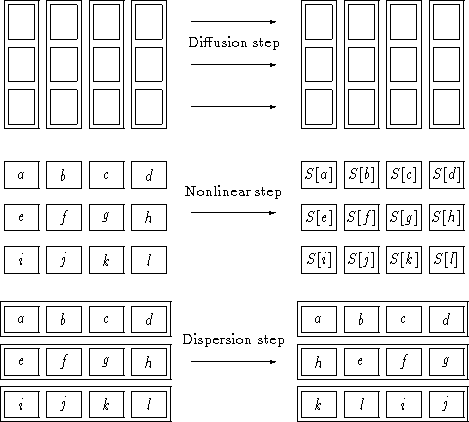 Figure 1: Graphical illustration of some basic operations of the Square ciphers.
Figure 1: Graphical illustration of some basic operations of the Square ciphers.
The choice for the operations in the different steps has been influenced by
our wish to make the cipher efficiently implementable on Smartcards.
The key addition, the dispersion and the nonlinear step all can be implemented
using operations on individual bytes, the natural ``unit'' on an 8-bit
processor. In the diffusion step, inter-byte diffusion has to be realised.
On a 32-bit processor, this can be done by using operations like 32-bit rotations,
multiplications, ..., but the use of these operations complicates
Smartcard implementations.
In the Square family, the diffusion step can be described as a matrix multiplication (cf. Section 3).
The coefficients of the multiplication matrix have been selected carefully to provide
diffusion that is optimal in a very definite, mathematical sense, while at the same
time allowing very efficient implementation on standard Smartcard processors.
2.2 The key schedule
The round keys have length n and r+1 round keys are required:
one for every round and a final key addition. The key schedule can be thought
to occur in two phases.
- Generation of the expanded key:
- The expanded key is initialized by taking
the m-bit cipher key. It is expanded by iteratively attaching m-bit blocks that
are computed from the previously attached block by means of an LFSR-like computation.
This is repeated until the expanded key has length n(r+1).
- Extraction of round keys:
- Round key i is taken from the expanded key by
taking the i-th n-bit block.
The LFSR computations in the key expansion ensure that any pair of different cipher keys
result in a pair of expanded keys with a large Hamming difference. The addition of
round constants removes symmetry between the rounds. This is necessary in order to
provide resistance against related-key attacks and attacks where the cipher key is
known, e.g., if the cipher is used as the compression function of a hash function.
3 Specific Smartcard implementation aspects
In this section we discuss the implementation of the cipher on 8-bit processors
with a limited amount of RAM and ROM available, i.e., typical Smartcard processors.
3.1 The round transformation
The round transformation
can be implemented by serially performing the different steps.
The nonlinear step consists of a table lookup operation that is the same
for all input bytes. The 256-byte lookup table is hard-coded in the cipher
program and the table lookup can be implemented with a simple load accumulator
instruction in indexed mode. The round key addition is implemented with the
EXOR instruction. The byte dispersion step does not take dedicated instructions
but is embodied in the way input bytes are loaded and stored in the
preceding/succeeding steps. These three steps can be implemented in the
following way: the byte is loaded into the index register, an indexed load
accumulator instruction is performed, the round key byte is EXORed
and the accumulator is stored to the (hard coded) location.
Implementing the diffusion step is less straightforward. It takes the
computation of additions and multiplication in the field GF(28).
Addition over this field corresponds to the readily available EXOR instruction.
The multiplication factors are the elements of GF(28) represented by byte
values 1, 2 and 3. The multiplication by these factors can be done as follows:
- 1 is the identity in GF(28) and multiplication by it does not
require any computation at all.
- Multiplication by 2 in the finite field could be implemented as a left shift,
followed by a reduction. However, the execution time and/or the power consumption
pattern of a reduction depend on the value of the operand. If the MSB of the operand
is 1, the reduction takes place, if 0, the reduction can be skipped. This can be done in
constant time by executing dummy instructions (e.g., NOP) in the case the reduction is skipped.
However, this gives rise to two different sequences of operations. The operation can be
implemented with a fixed series of instructions by implementing the multiplication by 2 as a
table lookup with a dedicated lookup table 2mult[·], that is defined as
The fact that the execution time is independent of the argument makes this table lookup implementation timing attack resistant. We explain in Section 4
how it can be protected against power analysis.
- Multiplication by 3 can be obtained by performing multiplication with 2
and adding (EXORing) the argument itself:
3 ·a = (2 Å1) ·a = 2mult[a] Åa.
In Rijndael and Square the columns consist of 4 bytes each and the diffusion
step applied to a column can be described by a matrix multiplication,
that is given by:
|
|
é
ê
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
ú
û
|
= |
é
ê
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
ú
û
|
· |
é
ê
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
ú
û
|
. |
|
This can be efficiently implemented as:
|
| |
|
|
| |
|
|
2mult[in0 Åin1] ; out0 Å = p Åin0 ; |
| |
|
|
2mult[in1 Åin2] ; out1 Å = p Åin1 ; |
| |
|
|
2mult[in2 Åin3] ; out2 Å = p Åin2 ; |
| |
|
| 2mult[in3 Åin0] ; out3 Å = p Åin3 ; |
|
| |
|
This implementation takes only 15 EXORs and 4 table lookups per column.
It requires temporary storage for 2 bytes: the variables p and in0
(if the output buffer is equal to the input buffer).
In BKSQ the columns consist of 3 bytes and the diffusion step is given by
|
|
é
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
û
|
= |
é
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
û
|
· |
é
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
û
|
. |
|
This can be implemented with only 5 EXORs and a single table lookup per column and
only one byte of temporary storage is needed.
3.2 The inverse round transformation
The Square ciphers do not have the Feistel structure, like e.g. the DES.
Whereas for Feistel ciphers the operation of the cipher can be inverted by simply
reordering the round keys, this is not possible for the Square ciphers.
Therefore, if the inverse operation of the cipher has to be implemented, it
is necessary to implement the inverse round operation separately.
The inverse of the round key addition is the same as the round key addition: EXOR
with the round key. The inverse of the nonlinear step is implemented like the
linear step, but uses a different lookup table. The byte dispersion step is
again embodied in the way input bytes are loaded and stored in the other steps.
The inverse of the diffusion step consists of a multiplication with the
inverse matrix. For Rijndael and Square, the inverse of the diffusion step is
given by:
|
|
é
ê
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
ú
û
|
= |
é
ê
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
ú
û
|
· |
é
ê
ê
ê
ê
ê
ë
|
|
| |
ù
ú
ú
ú
ú
ú
û
|
. |
|
Here B, D and E denote hexadecimal values. It is easy to see
that this multiplication will require more operations than the original diffusion
step, namely 21 EXORS and 8 table lookups
using only the previously defined table 2mult[·].
If additional tables are used, the performance loss can be reduced.
The storage requirements do not increase.
Note that most applications do not require the inverse operation of the
cipher to be executed on the Smartcard. First of all, most of the applications use
the cipher for the generation and verification of MACs and as a one-way function
in the generation of session keys. In the cases where encipherment is actually used,
the CFB or OFB mode can be used, where the inverse cipher is not used.
3.3 The key schedule
In a Smartcard implementation, computing the expanded key in a single shot
and storing it for use during the actual encryption, would
require too much RAM. Therefore, the key expansion has been defined in such a way
that it can be implemented in a cyclic buffer with a size
no larger than the size of the cipher key.
The expansion operation has been kept very simple and efficient to
make fast just-in-time key generation possible.
In the case that the cipher key length is equal to the block length,
the round key is simply
updated in between rounds. In the other cases, a small amount of additional
sequence control is required.
All operations in the key update can be efficiently implemented using EXORs
and table lookups.
3.4 32-bit processors
On a 32-bit processor, an efficient implementation of the round
transformation will use four large tables (1k each) that combine the effect of
the nonlinear and the dispersion step.
The tables will fit nicely in the cache of most modern 32-bit processors.
The performance is independent of the value of the multiplication factors
in the dispersion step. The inverse operation of the cipher has the
same performance as the forward operation, but uses a different set of
tables.
4 Smartcard-specific attacks
Recently, several attacks have been demonstrated that exploit weaknesses of
cipher implementations, rather than the inherent mathematical properties of
the actual cipher [4]. These attacks exploit information such as
timing and power consumption to obtain information on the cipher key or
plaintext. In this section we will explain that the ciphers of the Square
family lend themselves to implementations that provide resistance against
this type of attack typical for Smartcards.
If programmed as explained in the previous section, the cipher execution
consists of a series of instructions that is completely fixed: there are
no conditional branches whose execution depends on the cipher key and input.
This thwarts the following attacks:
- Timing attack:
- This attack extracts key/plaintext information from the
CPU time consumed by the cipher. For the Square ciphers the CPU time is
independent of the cipher key and plaintext.
- Simple power analysis:
- This attack extracts key/plaintext information
by observing the power consumption during the cipher computation. Different CPU
instructions have different power consumption and this attack allows to determine
whether one or another conditional branch is taken in a computation. For the
Square ciphers the series of instructions is fixed.
A more powerful attack is differential power analysis. This attack exploits the
fact the power consumed by the CPU not only depends on the instruction that is
executed, but also on the values of the operands. It combines the application
of cryptanalytic techniques, statistics and power analysis.
Basically, it allows the determination of the value of individual bits of
intermediary computation results of the cipher by an attacker that does not
even need to know the sequence of instructions. The basic flaw that is exploited
is that the power consumed by an instruction depends on the values of the bits
that are handled by the command. To thwart these attacks, two mechanisms are proposed:
- scrambling:
- To complicate the exploitation of power consumption bias, e.g.,
by using programming tricks, such as insertion of a variable amount of NOPS,
or better, unnecessary instructions in between rounds. Scrambling can be applied
reasonably independent from the cipher structure.
- curing:
- To make the power consumption of the relevant instructions used in
a cipher implementation much less dependent on the value of the treated bits.
One plausible way to cure instructions is by the introduction of symmetry.
For example: if a bit is stored in (loaded from) RAM, also store (load)
its complement. If two bits are EXORed, execute all four different combinations:
a Åb, [`a] Åb, a Å[`b], [`a] Å[`b]).
Typically, additional hardware has to be introduced for every sensitive instruction.
Therefore it is an advantage to have few different instructions that handle
key- or plaintext-dependent bits.
The instructions that handle key- or plaintext dependent bits in our implementations
of the ciphers of the Square family are:
- EXOR with accumulator, direct addressing;
-
store accumulator, direct addressing;
-
load accumulator, direct addressing;
-
load accumulator, indexed addressing (offset + index register)
These are only four instructions. Most other modern ciphers [5] use an instruction
set that is substantially larger, due to the use of arithmetic operations. Moreover, the
balancing of arithmetic operations is likely to be more complicated than the balancing of
the EXOR. It can be seen that there is arithmetic addition in the indexed addressing.
However, if the lookup tables are positioned at physical addresses that are a multiple of
256, the address computation can be reduced to a mere concatenation of index and offset.
Obviously, this implies a modification of the ALU hardware.
5 Performance
We implemented the Square ciphers on two different types of microprocessors that
are representative for Smartcards in use today. These implementations have been
optimized towards minimal RAM usage and execution time while guaranteeing a fixed
execution time. Table 1 shows that besides the storage of the current
round key and the intermediate ciphertext, only four bytes of RAM are used.
The numbers compare very favorably with the figures for the other AES
candidate algorithms.
The timings given include the key setup and algorithm setup time. Only the forward
operation of the ciphers have been implemented, backwards operation is expected to
be slower because the inverse of the diffusion step cannot be implemented as
efficiently (cf. Section 3.2). The inverse diffusion step is
between 1.5 and 2 times slower than the original diffusion step.
Since the diffusion step is dominant in the execution of the ciphers
on a Smartcard, about the same performance loss can be expected for the full
cipher.
The implementations on the Motorola 68HC08 microprocessor have been done using
the 68HC08 development tools by P&E Microcomputer Systems, Woburn, MA USA,
the IASM08 68HC08 Integrated Assembler and the SIML8 68HC08 simulator. No
optimization of code length has been attempted for this processor. Execution
time, code size and required RAM for a number of implementations are given in
Table 1 (1 cycle = 1 oscillator period = 0.25 msec).
| Cipher | Code size | Required RAM | Number of cycles | Execution time |
| (Key, block length) | (bytes) | (bytes) | | (msec) | |
| | BKSQ(96,96) | 900 | 28 | 6500 | 1.6 |
| Square(128,128) | 919 | 36 | 6800 | 1.7 |
| Rijndael(128,128) | 919 | 36 | 8390 | 2.1 |
| Rijndael(192,128) | 1170 | 44 | 10780 | 2.7 |
| Rijndael(256,128) | 1135 | 52 | 12490 | 3.1 |
Table 1:
Code size, required RAM and execution time for
the square ciphers in Motorola
68HC08 Assembler.
Rijndael has also been implemented on the Intel 8051 microprocessor,
using 8051 Development tools of Keil Elektronik: mVision IDE for Windows
and dScope Debugger/Simulator for Windows.
Execution time for several code sizes is given in Table 2
(1 cycle = 12 oscillator periods = 1 msec).
| (Key, block length) | Code size | Number of cycles | Execution time |
| (bytes) | | (msec) | |
| | 768 | 4065 | 4.1 |
| (128,128) | 826 | 3744 | 3.7 |
| 1016 | 3168 | 3.2 |
| (192,128) | 1125 | 4512 | 4.5 |
| (256,128) | 1041 | 5221 | 5.2 |
Table 2:
Code size and execution time
for Rijndael in Intel
8051 assembler.
6 Availability
Several
implementations of Square in C and Java are available from the URL
http://www.esat.kuleuven.ac.be/ ~rijmen/square.
More information on Rijndael and a reference implementation are available
from the URL
http://www.esat.kuleuven.ac.be/ ~rijmen/rijndael .
References
- [1]
- J. Daemen, L.R. Knudsen, V. Rijmen,
``The Square encryption algorithm,'' Dr. Dobb's Journal, Vol. 22,
No. 10, October 1997, pp. 54-56.
- [2]
- J. Daemen and V. Rijmen, ``The Rijndael block cipher,''
presented at the First Advanced Encryption Standard Conference,
Ventura (California),
1998, available from URL http://www.nist.gov/aes.
- [3]
- J. Daemen and V. Rijmen, ``The Block Cipher BKSQ,''
Proc. of CARDIS'98, LNCS, Springer-Verlag, to appear.
- [4]
- P.C. Kocher, ``Timing attacks on implementations of Diffie-Hellman,
RSA, DSS and other systems,'' Advances in Cryptology,
Proceedings Crypto'96, LNCS 1109, N. Koblitz, Ed.,
Springer-Verlag, 1996, pp. 146-158.
- [5]
- NIST's AES Homepage: http://www.nist.gov/aes.
Footnotes:
1 F.W.O. Postdoctoral researcher,
sponsored by the Fund for Scientific Research - Flanders (Belgium).
File translated from TEX by TTH, version 2.00.
On 16 Mar 1999, 11:54.
|
