|
USENIX '05 Paper
[USENIX '05 Technical Program]



Adaptive Main Memory Compression
Irina Chihaia Tuduce and Thomas Gross
Departement Informatik
ETH Zürich
CH 8092 Zürich, Switzerland
Abstract:
Applications that use large data sets frequently exhibit poor
performance because the size of their working set exceeds the real
memory, causing excess page faults, and ultimately exhibit thrashing
behavior.
This paper describes a memory compression solution to this problem
that adapts the allocation of real memory between uncompressed and
compressed pages and also manages fragmentation without user
involvement. The system manages its resources dynamically on the basis
of the varying demands of each application and also on the situational
requirements that are data dependent. The technique used to localize
page fragments in the compressed area allows the system to reclaim or
add space easily if it is advisable to shrink or grow the size of the
compressed area.
The design is implemented in Linux, runs on both 32-bit and 64-bit
architectures, and has been demonstrated to work in practice under
complex workload conditions and memory pressure. The benefits from our
approach depend on the relationship between the size of the compressed
area, the application's compression ratio, and the access pattern of
the application. For a range of benchmarks and applications, the
system shows an increase in performance by a factor of 1.3 to 55.
Many applications require more main memory to hold their data than a
typical workstation contains. Although the amount of main memory in a
workstation has increased with declining prices for semiconductor
memories, application developers have even more aggressively increased
their demands. Unfortunately, an application must resort to swapping
(and eventually, thrashing) when the amount of physical memory is less
than what the application (resp. its working set) requires.
Substantial disk activity eliminates any benefit that is obtained
from increased processor speed. Since the access time of a disk
continues to improve more slowly than the cycle time of processors,
techniques to improve the performance of the memory system are of
great interest to many applications.
Compression has been used in many settings to increase the effective
size of a storage device or to increase the effective bandwidth, and
other researchers have proposed to integrate compression into the
memory hierarchy. The basic idea of a compressed-memory system is to
reserve some memory that would normally be used directly by an
application and use this memory region instead to hold pages in
compressed form. By compressing some of the data space, the effective
memory size available to the applications is made larger and disk
accesses are avoided. However, since some of the main memory holds
compressed data, the applications have effectively less uncompressed
memory than would be available without compression.
The potential benefits of main memory compression depend on the
relationship between the size of the compressed area, an application's
compression ratio, and an application's access pattern. Because
accesses to compressed pages take longer than accesses to uncompressed
pages, compressing too much data decreases an application's
performance. If an application accesses its data set such that
compression does not save enough accesses to disk, or if its pages do
not compress well, compression will show no benefit. Therefore,
building the core of a system that adaptively finds the size of the
compressed area that can improve an application's performance is
difficult, and despite its potential to improve the performance of
many applications, main memory compression is considered only by few
application developers.
This paper presents an adaptive compressed-memory system designed to
improve the performance of applications with very large data sets
(compression affects only the data area). The adaptive resizing
scheme finds the optimal size of the compressed area automatically.
Because the system must be effective under memory pressure, it uses a
simple resizing scheme, which is a function of the number of free
blocks in the compressed area (this factor captures an application's
access pattern as well). For a set of benchmarks and large
applications, measurements show that the compressed area size found by
our resizing scheme is among those that improve performance the most.
We allocate and manage the compressed area such that it can be resized
easily, without paying a lot to move live fragments around. The key
idea is to keep compressed pages in zones; the use of zones
impose some locality on the blocks of a compressed page, such that the
system can easily reclaim or add a zone if it is advisable to shrink
or grow the compressed area size.
We examine three simulators that have different access patterns: a
model checker, a network simulator, and a car traffic
simulator. Depending on their input, the simulators allocate between a
few MB and several GB. In this paper, we experiment with inputs that
allocate between 164 MB and 2.6 GB. The measurements show that memory
compression provides enough memory to these classes of applications to
finish their execution on a system with a physical memory smaller than
is required to execute without thrashing, and execution proceeds
significantly faster than if no compression was used.
Because most of the application developers are mainly interested in a
design that works with a stock processor and a commodity PC, we
restrict the changes to the software system. The compressed-memory
system described here is implemented as a kernel module and patches
that hook into the Linux kernel to monitor system activity and control
the swap-in and swap-out operations. By restricting the changes to
the software system, we can use compression only for those
applications that benefit from it. The compressed-memory prototype
runs on 32-bit as well as on 64-bit architectures.
Integrating transparent adaptive memory into an operating system
raises a number of questions. The design presented here has been
demonstrated to work in practice. By choosing a suitable system
structure, it is possible to allow the memory system to adapt its size
in response to application requirements (an essential property for a
transparent system), and by choosing a simple interface to the base
operating system, it is possible to limit kernel interaction
(essential for acceptance by a user community).
2 Related Work
Several researchers have investigated the use of compression to reduce
paging by introducing a new level into the memory hierarchy. The key
idea, first suggested by Wilson [15], is to hold
evicted pages in compressed form in a compressed area, and intercept
page faults to check whether the requested page is available in
compressed form before a disk access is initiated. The
compressed-memory systems can be classified in software- and
hardware-based approaches. Since we want our solution to work with
stock hardware, we consider only software-based approaches. For a
description of the hardware-based approaches, we refer the interested
reader to a study by Alameldeen and Wood [3].
The software-based approaches can be either adaptive or static. The
adaptive approaches vary the size of the compressed area dynamically,
and are either implementation- or simulation-based
investigations. Douglis' early paper [7] adapts
the compressed area size based on a global LRU scheme. However, as
Kaplan [10] shows latter, Douglis' adaptive
scheme might have been maladaptive. Douglis implemented his adaptive
scheme in Sprite and showed that compression can both improve (up to
62.3%) and decrease (up to 36.4%) an application's performance.
Castro et al. [6] adapt the compressed area size
depending on whether the page would be uncompressed or on disk if
compression was not used. The main drawback of their scheme is that it
must analyze every access to the compressed area, and although the
approach may work well for small applications, it may not be feasible
for large applications with frequent data accesses. The authors
implemented their scheme in Linux and report performance improvements
of up to 171% for small applications. Wilson and
Kaplan [16,10] resize the
compressed area based on recent program behavior. The authors maintain
a queue of referenced pages ordered by their recency information. The
main drawback of their scheme is that it is based on information
(about all pages in the system) that cannot be obtained on current
systems; the authors use only simulations to validate their solution.
Moreover, as the physical memory size increases, the size of the page
queue increases as well, making this approach unsuitable for
applications running on systems with large memories.
Static approaches use fixed sizes of the compressed area. Although
these studies are useful to assess the benefits of memory compression,
they fail to provide a solution that works for different system
settings and applications. Cervera et al. [4]
present a design implemented in Linux that increases an application's
performance by a factor of up to 2 relative to an uncompressed swap
system. Nevertheless, on a system with 64 MB physical memory, only
4 MB are allocated to the compressed data, and this small area may not
suffice for programs with large working sets. Kjelso et
al. [11,12] use simulations to
demonstrate the efficacy of main memory compression. The authors
develop a performance model to quantify the performance impact of a
software- and hardware-based compression system for a number of
DEC-WRL workloads. Their results show that software-based compression
improves system performance by a factor of 2 and hardware-based
compression improves performance by up to an order of magnitude.
RAM Doubler is a technology that expands the memory size for Mac
OS [2]. It locates small chunks of RAM that
applications aren't actively using and makes that memory available to
other applications. Moreover, RAM Doubler finds RAM that isn't likely
to be accessed again, and compresses it. Finally, if all else fails,
the system swaps seldom accessed data to disk. Although RAM Doubler
allows the user to open more applications together, the user cannot
run applications with memory footprints that exceed the physical
memory size. Our work tries to provide enough memory to large
applications so that they can run to completion when their memory
requirements exceed the physical memory size.
A compressed-memory system divides the main memory into two areas: one
area holds uncompressed pages and the other area (compressed
area) holds pages in compressed form. When an application's working
set exceeds the uncompressed area size, parts of the data set are
compressed and stored in the compressed area. When even the compressed
area becomes filled, parts of the compressed data are swapped to
disk. On a page fault, the system checks for the faulted page in the
compressed area before going to the disk, servicing the page from that
area if it is there and saving the cost of a disk access.
The key idea of our compressed-memory design is to organize the
compressed area in zones of the same size that are linked in a
zone chain, as shown in Figure 1. As the
size of the compressed area grows and shrinks, zones are added and
removed from the chain. The system uses a hash table for
tracking all pages that are stored in the compressed area. If a page
is in the compressed area, its entry in the hash table points to
the zone that stores its compressed data. Moreover, the system uses a
global double-linked LRU list for storing the recency information of
all compressed pages. LRU first and LRU last identify the
first and last page in the LRU list.
A zone has physical memory to store compressed data and structures to
manage the physical memory. A zone's physical data and its structures
are allocated/deallocated when a zone is added/deleted. To keep
fragmentation as low as possible, a zone's physical memory is divided
in blocks of the same size. A compressed page is stored as a list of
blocks that are all within the same zone. Each zone uses a block
table for keeping track of its blocks and their usage information.
Furthermore, each zone uses a comp page table for mapping
compressed pages to their data blocks, as shown in
Figure 2. The number of entries in comp page
table gives the maximum number of compressed pages that can be stored
in a zone, and is equal with a compression factor multiplied
with the number of pages that can be stored in a zone if no
compression is used. The following subsections elaborate on how pages
are stored and found in the compressed area, as well as how the
compressed area is resized.
Figure 1:
Birdseye view of the compressed-memory system design.
 |
When a page is evicted from the uncompressed area, it is compressed
and stored in a compression buffer. The system searches for the first
zone that has enough blocks to store the compressed page (the
allocation is basically the first-fit algorithm). The system selects
a zone from the zone chain and uses the used field of the
zone structure to check the number of free blocks in that zone
(see Figure 2). If the number of free blocks is
insufficient to store the compressed page, another zone is selected
and the test is repeated. If the zone has sufficient free blocks, the
system uses the free entry field of the zone structure to
select an entry in the comp page table. All free entries are
linked using the next field and the free entry field
identifies the first element in the list. The selected entry will
store information about the new compressed page.
After a zone to store the compressed page is found, the system selects
as many blocks as needed to store the compressed data. The system
traverses the list of free blocks (whose beginning is identified by
the free block field) and selects the necessary number of free
blocks. All free blocks are linked in a chain by their next
field in the block table. The value of the free block
field of the zone structure is updated to point to the block
following the last block selected. The compressed page is now copied
into the selected blocks, and the first field of the selected
entry is set to point to the first block that stores the compressed
page. The selected blocks are still linked by their next field,
and therefore all the blocks that store a compressed page are linked
in a chain. The values of the swap handle and the size of
the compressed page are also set. The LRU next and previous
fields of the selected entry are now set, and LRU first and
LRU last are updated.
The system computes the index of the new compressed page in the
hash table. All entries that map to the same index (hash value) are
linked in a chain stored in the next field of their entries in
the comp page table. The first element in the chain is
identified by the value stored in the hash table. The new
compressed page is inserted at the beginning of the chain and its
hash table entry is updated.
Figure 2:
Detailed view of the compressed-memory system design.
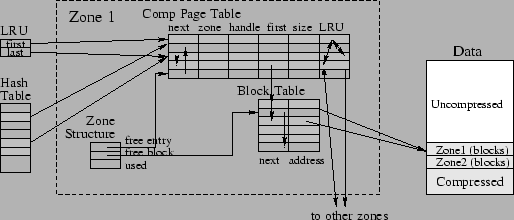 |
On a page fault, the system uses the hash table to check whether
the faulted page is in the compressed area. If the page is
compressed, it is decompressed, its blocks are added to the free list
of blocks, its entry in the comp page table can be reused, the
zone structure and the hash table entry are updated. If
the page is not in the compressed area (does not have an entry in the
hash table), it is brought from disk into the uncompressed
memory.
Because pages are not scattered over multiple zones, when a page is
inserted or deleted, the system does not have to keep track of
multiple zones that store a page's data. Moreover, when a zone is
deleted, the system must not deal with pages that are partially stored
in other zones. Therefore, by storing all the blocks of a compressed
page within a single zone, we avoid the scatter/gather problem
encountered by Douglis [7].
When the compressed area becomes (almost) filled, its LRU pages are
sent to disk, and the number of free compressed pages is kept above a
configurable threshold. Although it is possible to transfer
variable-size compressed pages to and from disk, implementing
variable-size I/O transfers requires many changes to the
OS [7]. To take advantage of the swap mechanism
implemented in the OS, we choose to store uncompressed pages on the
disk. Moreover, if the page is stored in compressed form,
the next time this page is swapped in, it must be first decompressed
before
it can be used. Therefore, to lower the latency of a future access and to
employ the OS swapping services, we
decompress a page before sending it to disk.
The system presented here grows and shrinks the compressed area while
applications execute. The resizing decision is based on the amount of
data in the compressed area. The system monitors the compressed area
utilization. When the amount of memory in the compressed area is above
a high threshold, the compressed region is grown by adding a
zone. When the amount of memory used is below a low threshold, the
compressed area is shrunk by deleting a zone. As long as the amount of
memory used is above the low threshold and bellow the high threshold,
the size of the compressed area remains the same.
All the zones in the system are linked in the zone chain, and
new zones are added at the end of the chain. When a page is inserted
in the compressed area, it is stored in the first zone from the
beginning of the zone chain that has enough space to store the
compressed data. To shrink the compressed area, the system deletes
the zone with the smallest number of blocks used (to keep the overhead
as low as possible). The compressed pages within the zone to be
deleted are relocated within other zones (using again the first-fit
algorithm). When the free space within other zones is too small to
store the pages to be relocated, some compressed pages are swapped to
disk. To grow the compressed area, the system allocates space for a
new zone. Because the OS may not have enough free space for the new
zone, some uncompressed pages will be compressed and stored in
compressed form. At that time, some compressed pages may be swapped to
disk to make room for the newly compressed pages. (The LRU order is
always preserved.)
In this section, we give an overview of our implementation of the
compressed-memory system in Linux. We use Yellow Dog Linux 3.0.1
(YDL) that is built on the 2.6.3 Linux kernel and provides 64-bit
support for the Apple G5 machines. The prototype works on both 32-bit
and 64-bit architectures, and we installed it on a Pentium 4 PC and on
a G5 machine. Although the discussion of our solution is necessarily
OS-specific, the issues are general.
Our design is implemented as a loadable module, along with hooks in
the operating system to call module functions at specific
points. These points are swapping in pages, swapping out pages, and
deactivating a swap area. We use a hierarchy of locks and semaphores
to protect our code against race conditions. The prototype implements
four de/compression algorithms commonly used to de/compress in-memory
data: WKdm, WK4x4, LZRW1, and LZ0 [16]. The
implementation comprises of about 5,000 lines of C code.
We implemented a performance monitor that collects information about
large applications and decides whether to turn on compression. The
tool resizes the compressed area dynamically. This tool is implemented
in user-space and uses a small library to interact with the kernel
module. The implementation of the monitor and library comprises of
about 1,200 lines of C code.
A kernel module can allocate only kernel memory and is not involved
in handling segmentation and paging (since the kernel offers a
unified memory management interface to drivers). In Linux, the
kmalloc() function allocates a memory region that is contiguous
in physical memory. Nevertheless, the maximum memory size that can be
allocated by kmalloc() is 128 KB [13]. Therefore,
when dealing with large amounts of memory a module uses the
vmalloc() function to allocate non-contiguous physical memory
in a contiguous virtual address space. Unfortunately, also the memory
size that can be allocated by vmalloc() is limited, as
discussed in the next paragraph.
Figure 3:
Linux kernel space.
 |
The Linux kernel splits its address space in two parts: user space and
kernel space [8]. On x86 and SPARC architectures, 3 GB are
available for processes and the remaining of 1 GB is always mapped by
the kernel. (The kernel space limit is 1 GB because the kernel may
directly address only memory for which it has set up a page table
entry.) From this 1 GB, the first 8 MB are reserved for loading the
kernel image to run, as shown in Figure 3. After the
kernel image, the mem_map array is stored and its size depends on the
amount of available memory. In low-memory systems (systems with less
than 896 MB), the remaining amount of virtual address space (minus a 2
page gap) is used by the vmalloc() function, as shown in
Figure 3.a. For illustration, on a Pentium 4 with 512 MB
of DRAM, a module can allocate about 400 MB. In high-memory systems,
which are systems with more than 896 MB, the vmalloc region is followed
by the kmap region (an area reserved for the mapping of high-memory
pages into low memory) and the area for fixed virtual address
mappings, as shown in Figure 3.b. On a system with a lot
of memory, the size of the mem_map array can be significant, and not
enough memory is left for the other regions. As the kernel needs these
regions, on x86 the vmalloc area, the kmap area, and the area for
fixed virtual address mapping is defined to be at least 128 MB; this
area is denoted by VMALLOC_RESERVE at minimum. For
illustration, on a Pentium 4 with 1 GB of DRAM, a module can allocate
100 MB. Nevertheless, for applications with large memory footprints, a
compressed area of 10% is insufficient. 64-bit architectures aren't
as limited in memory usage as 32-bit architectures; a module can
allocate 2TB on a 64-bit PowerPC that runs Linux in 64-bit mode.
Because vmalloc() is a flexible mechanism to allocate large
amounts of data in kernel space, we use vmalloc() to allocate
memory for the entire compressed area: for the hash table, physical
memory, zone structure, comp page table, and block table.
To allow off-line configuration, we have also implemented a
compressed-memory system that uses the bigphysarea
patch [1] to allocate very large amounts of memory
to the compressed data. This unofficial patch has been floating
around the Net for years; it is so renowned and useful that some
distributions apply it to the kernel images they install by default.
The patch basically allocates memory at boot time and makes it
available to device drivers at runtime. Although boot-time allocation
is inelegant and inflexible, it is the only way to bypass the limits
imposed by the 32-bit architecture on the size of the vmalloc
region [13].
The compressed-memory page daemon (kcmswapd) is responsible for
swapping out pages, so that we have some free memory in the compressed
area. The kcmswapd kernel thread is started when memory
compression is enabled and is activated on compressed-memory
pressure. kcmswapd is started after the decision to shrink the
compressed area is taken. The daemon swaps out enough compressed pages
to make space for the pages stored within the zone to be deleted
(these pages have to be relocated within and/or outside the compressed
area). Moreover, kcmswapd makes space for the uncompressed
pages that have to be swapped out to make space for the new zone when
the compressed area grows.
5 Evaluation
We select a set of benchmarks and applications that have different
memory requirements and access patterns. We conduct a set of
experiments to determine how much can a system win from employing
memory compression, how much can it lose, and how good the adaptive
resizing scheme is.
We use Yellow Dog Linux 3.0.1 (YDL) in 32-bit mode to experiment with
benchmarks and applications that run on 32-bit architectures. The
system used is a Pentium 4 at 2.6 GHz with a 8 KB L1 data cache, 512 KB
L2 cache and 1 GB DRAM; this PC has its swap partition on a
IC35L060AVV207-0 ATA disk. Given the memory usage limitations of the
32-bit architectures, to experiment with applications that need
compressed areas larger than 100 MB we use an Apple G5 machine that
runs YDL in 64-bit mode. The Apple G5 has a dual 64-bit PowerPC 970
microprocessor at 1.8 GHz with a 32 KB L1 data cache, 512 KB L2 cache
(per processor) and 1 GB or 1.5 GB DRAM, and has its swap partition on a
ST3160023AS ATA disk. For all experiments, we use the WKdm compression
algorithm as it shows superior performance over other
algorithms [16]. The systems have a block size of
128 bytes, a zone size of 4 MB, and a compression factor of 4. (A
compression factor of 4 means that the system can store 4 times more
pages within a zone than if no compression was used.)
The first benchmark shows how much can memory compression degrade
system performance. The benchmark, called thrasher, pays the
cost of compressing pages without gaining any benefit. The benchmark
cycles linearly through its working set reading and writing the whole
data space. Because Linux uses an LRU algorithm for page replacement,
if thrasher's working set doesn't fit in memory, it takes a page
fault on each page each time it iterates through the working set.
Moreover, each page fault requires a disk read as well as a page write
to make room for the faulted page, and we have also the overhead of
compressing pages. Because of its access pattern, thrasher will
always require pages from disk and will never fault on compressed
pages. We set the thrasher's working set size to 1.2 GB and we
measure its execution time when the size of the physical memory is 1 GB
and the compressed area has fixed sizes between 50 MB and 100 MB;
thrasher has a compression ration of 50% (or 1:2), which is common
for many applications. For this set-up the benchmark executes up to 3
times slower than without compression on the Apple G5 and up to 2
times slower on the Pentium 4 PC.
Programs that use dynamic memory allocation access their data through
pointers, and hence have irregular access patterns. To investigate
the performance of such an application (e.g., written in C++) we use a
second benchmark, called rand. The advantage of the benchmark
over a real application is that its memory footprint and number of
data accesses can be changed easily. The benchmark reads and writes
its data set randomly and has a compression ration of 50%. We
consider three variants that allocate 1.2 GB, 1.4 GB, and 1.8 GB and
access their data sets 200,000, 1,200,000, and 6,000,000 times; we
execute the benchmark on an Apple G5 with 1 GB physical memory. The
three variants finish execution in 538.62 sec, 5,484.75 sec, and
47,617.38 sec. When we apply our adaptive compression technique to
these variants their performance improves by a factor of 3.66, 11.88,
and 18.96; the compressed area size found by the resizing scheme is
64 MB, 96 MB, and 140 MB.
SMV is a method based on Binary Decision Diagrams (BDDs) used for
formal verification of finite state systems. We use Yang's SMV
implementation since it demonstrated superior performance over other
implementations [17]. We choose different SMV inputs that
model the FireWire protocol [14]. SMV's working set is
equal to its memory footprint (SMV uses all the memory it allocates
during its execution rather than a small subset) and has a compression
ratio of 52% on average.
We consider an SMV model, nodes_2_4_3, with a small memory
footprint of 164 MB, to explore the limitations of compressed
memory. An application with such a small footprint is unlikely to
require compression but allows us to perform many experiments. We
conduct the first set of experiments on the Pentium 4 PC at
2.6 GHz. We configure the system such that the amount of memory
available is 97% to 73% of memory allocated. The measurements are
summarized in Table 1, column ``W/o compr." and show that
when physical memory is smaller than SMV's working set, SMV's
performance is degraded substantially. In the next set of experiments,
SMV executes on the adaptive compressed-memory system. The
measurements are summarized in Table 1, column ``W/
compr.", and indicate that when the amount of memory available is 87%
to 73% of memory allocated, our adaptive compression technique
increases performance by a factor of up to 4. The measurements also
show that for this small application when the memory shortage is not
big enough (memory available is 97% to 92% of memory allocated),
taking away space from the SMV model for the compressed area will
slowdown the application.
Table 1:
Execution time of nodes_2_4_3 model on a Pentium 4 PC at 2.6 GHz.
| Memory |
W/o compr. |
W/ compr. |
| available |
sec |
slowdown |
sec |
speedup |
| 100% |
6 |
- |
6 |
- |
| 97% |
10 |
1.66 |
16 |
0.62 |
| 92% |
16 |
2.66 |
65 |
0.24 |
| 87% |
403 |
67.16 |
391 |
1.03 |
| 85% |
1,307 |
217.83 |
450 |
3.22 |
| 82% |
2,431 |
405.16 |
791 |
3.07 |
| 80% |
3,601 |
600.16 |
1,175 |
3.06 |
| 78% |
4,645 |
774.16 |
1,433 |
3.24 |
| 75% |
5,649 |
941.50 |
1,609 |
3.51 |
| 73% |
8,789 |
1,464.83 |
2,177 |
4.03 |
|
We repeat the experiments on the Apple G5 that has a different
architecture and a 1.8 GHz processor, and we summarize the results in
Table 2. (Different DRAM chips we use have a negligible
influence of 0.02% on an application's performance.) The results for
the adaptive set-up, summarized in column ``W/ compr.", indicate that
when SMV executes on the G5 machine with the compressed-memory system
described here, SMV's performance improves by a factor of up to
3. Overall, the results indicate that on a slow machine (Apple G5),
compression improves performance for a smaller range of configurations
than on a fast machine (Pentium 4 at 2.6 GHz). The measurements
confirm other researchers' results: on older machines memory
compression can increase system performance by a factor of up to 2
relative to an uncompressed swap
system [4,12,6]. Moreover,
our measurements show that memory compression becomes more attractive
as the processor speed increases.
Table 2:
Execution time of nodes_2_4_3 model on an Apple G5 at 1.8 GHz.
| Memory |
W/o compr. |
W/ compr. |
| available |
sec |
slowdown |
sec |
speedup |
| 100% |
10 |
- |
10 |
- |
| 97% |
37 |
3.7 |
32 |
1.15 |
| 92% |
47 |
4.7 |
71 |
0.66 |
| 87% |
290 |
29 |
1,045 |
0.27 |
| 85% |
1,212 |
121 |
1,270 |
0.95 |
| 82% |
2,165 |
216 |
1,382 |
1.56 |
| 80% |
3,290 |
329 |
1,508 |
2.18 |
| 78% |
4,900 |
490 |
1,670 |
2.93 |
| 75% |
5,650 |
565 |
1,931 |
2.92 |
| 73% |
6,780 |
678 |
2,233 |
3.03 |
|
NS2 is a network simulator used to simulate different protocols over
wired and wireless networks. We choose different inputs that simulate
the AODV protocol over a wireless network. NS2's working set is
smaller than its memory footprint (it uses only a small subset of its
data at any one time) and has a compression ratio of 20% (or 1:5) on
average. The amount of memory allocated by a NS2 simulation is
determined by the number of nodes simulated, and the size of the
memory used is given by the number of traffic connections that are
simulated.
We consider two simulations that allocate 880 MB and 1.5 GB. We
configure the system such that the amount of memory provided is less
than memory allocated, and we measure the simulations' execution time
and compute their slowdown. The results are summarized in
Table 3, column ``W/o compr.", and show that when memory
available is 68% to 43% of memory allocated, NS2 executes slightly
slower than normal. When we apply our compression technique to NS2
executing with the same reduced memory allocation, its performance
improves by a factor of up to 1.4. The measurements for the adaptive
set-up are summarized in Table 3, column ``W/ compr.".
The results show that because NS2 allocates a large amount of data but
uses only a small subset of its data at any one time, compression does
not improve performance much, but fortunately, compression does not
hurt either.
Table 3:
NS2 execution time on an Apple G5 at 1.8 GHz.
| Working |
Memory |
W/o compr. |
W/ compr. |
| set size |
available |
sec |
slowdown |
sec |
speedup |
| 880 MB |
58% |
345 |
1.36 |
252 |
1.36 |
| |
50% |
426 |
1.69 |
313 |
1.36 |
| |
43% |
586 |
2.32 |
425 |
1.37 |
| 1.5 GB |
68% |
1,335 |
1.11 |
1,275 |
1.04 |
| |
62% |
1,351 |
1.12 |
1,215 |
1.11 |
|
The second set of experiments uses inputs that allocate 730 MB, 880 MB,
and 990 MB. We execute the selected simulations on a system with and
without compression when memory available is 70%, 68%, and 51% of
memory allocated, and we summarize the results in Table 4.
The data in column ``W/ compr." show that because NS2's working set is
small (smaller than memory allocated) and fits into small memories,
compression does not improve NS2's performance much. Overall, the
measurements show that on the faster Pentium 4 PC compression
improvements are slightly bigger than on the slower G5 machine.
Table 4:
NS2 execution time on an adaptive compressed-memory system.
| Working |
Memory |
W/o compr. |
W/ compr. |
| set size |
available |
sec |
sec |
speedup |
| Pentium 4 at 2.6 GHz |
| 730 MB |
70% |
145 |
128 |
1.13 |
| 880 MB |
58% |
205 |
168 |
1.22 |
| 990 MB |
51% |
275 |
197 |
1.39 |
| G5 at 1.8 GHz |
| 730 MB |
70% |
243 |
226 |
1.07 |
| 880 MB |
58% |
345 |
252 |
1.36 |
| 990 MB |
51% |
398 |
319 |
1.23 |
|
qsim [5] is a motor vehicle traffic simulator that
employs a queue to model the behavior of varying traffic conditions.
Although a simulation can be distributed on many computers (e.g., a
cluster), the simulation requires hosts with memory sizes bigger than
1 GB. For a geographic region, the number of travelers (agents)
simulated determine the amount of memory allocated to the simulation
and the number of (real) traffic hours being simulated gives the
execution time of the simulation.
We consider simulations that allocate 1.3 GB, 1.7 GB, 1.9 GB, and
2.6 GB and simulate the traffic on the road network of Switzerland.
We measure the execution time of these simulations on the G5 machine
without compression and with adaptive compression, and we summarize
the results in Table 5. The system has a block size of
128 bytes, a zone size of 4 MB, and a compression factor of 9. The
results in column ``W/ compr." show that when qsim executes on
our compressed-memory system, its performance improves by a factor of
20 to 55. qsim's working set is equal to its memory footprint
(during its execution, qsim uses all the memory it allocates),
and has a compression ratio of 10% (or 1:10) on average. Because
qsim compresses so well, even when the amount of memory provided is
much smaller than memory allocated, the simulation fits into the
uncompressed and compressed memory and finishes its execution in a
reasonable time. For instance, although the last simulation listed in
Table 5 allocates 2.6 GB, it succeeds to finish its
execution on a system with only 1 GB physical memory, and this would
not be possible without compression.
Table 5:
qsim execution time on an Apple G5 at 1.8 GHz.
| Working |
Physical |
W/o compr. |
W/ compr. |
| set size |
memory |
sec |
sec |
speedup |
| 1.3 GB |
1 GB |
3,993 |
135.45 |
29.47 |
| 1.7 GB |
1 GB |
24,580 |
513.66 |
47.85 |
| |
1.5 GB |
2,900 |
141.53 |
20.49 |
| 1.9 GB |
1 GB |
46,049 |
825.72 |
55.76 |
| |
1.5 GB |
11,456 |
277.91 |
41.22 |
| 2.6 GB |
1 GB |
51,569 |
988.01 |
52.19 |
| |
1.5 GB |
13,319 |
332.50 |
40.05 |
|
We repeat the simulation that allocates 1.9 GB on the Pentium 4 PC with
1 GB physical memory. On an Apple G5 with 1 GB physical memory the
system allocates 140 MB to the compressed data, but on the Pentium 4 PC
the compressed area can be 100 MB at most. The measurements show that
because the Pentium 4 PC fails to allocate enough memory to the
compressed data, the simulation executes 8.5 times slower than on the
Apple G5 (although the Pentium 4 processor is faster than the PowerPC
processor). This experiment shows the importance of a flexible OS
support: if the amount of memory that can be allocated in kernel mode
was not limited, main memory compression would improve the performance
of this large application considerably.
Our analysis examines the performance of three applications and shows
that compression improves the performance for all these applications,
but varies according to the memory access behavior and also to the
compression ratio employed.
SMV and qsim use their entire working set during the execution.
When the amount of memory provided is less than memory allocated by
10% or more, SMV executes approximately 600 times slower than without
swapping. The measurements show that when the amount of memory
available is 15% smaller than SMV's working set, our compression
technique provides an increase in performance by a factor of 3 to 4
depending on the processor used (a factor 3 for a G5 and 4 for a
Pentium 4). When we apply our compression techniques to qsim its
execution is improved by a factor of 20 to 55.
The NS2 simulator allocates a large amount of data but uses only a
small subset of its data at any one time, and thus provides an example
that is much different from SMV. Under normal execution (without the
aid of our compression techniques) when physical memory is 40%
smaller than memory allocated, NS2' execution is slowdown by a factor
of up to 2. When we apply our compression techniques to NS2 executing
with the same reduced memory allocation its performance improves by a
factor of up to 1.4.
Previous work determines the amount of data to be compressed by
monitoring every access to the compressed
data [10,16,6]. The
system keeps track of the pages that would be anyway in memory (with
and without compression) and pages that are in (compressed) memory
only because compression is turned on. The decision to shrink or grow
the compressed area is based on the number of accesses to these two
types of (compressed) pages. This approach succeeds to detect when the
size of the compressed area should be zero, which is not the case with
our resizing scheme (see Table 1, column ``W/ compr."
when memory available is 97% and 92% of memory allocated and
Table 2, column ``W/ compr." when memory available is
92%, 87%, and 85% of memory allocated). Nevertheless, for each
access to the compressed data, the system has to check whether the
page would be in memory if compression was turned off. To check this,
the system has to find the position of the page in the (LRU) list of
all compressed pages. Because to search a list of n pages takes
O(n) time in the worse case, this approach is not feasible for
applications with large data sets. We experimented with schemes that
monitor each access to the compressed data, and we found that the
check operations decrease system's performance by a factor of 20 to
30. To summarize, although previous resizing schemes succeed to detect
when compression should be turned off, they cannot be used for
applications with large data sets.
We take a different approach and adapt the compressed area size such
that the uncompressed and compressed memory contain most of an
application's working set. (For this scenario most of the
application's disk accesses are avoided.) Our approach is based on the
observation that when the compressed area is larger than an
application's memory footprint, some space within the compressed area
is unused. By default, compression is turned off and the system checks
the size of memory available periodically. If an application's memory
needs exceed a certain threshold, compression is turned on for that
application and a zone is added to the compressed area. From now on,
the system checks the amount of compressed data periodically and
decides whether to change the size of the compressed area.
If the amount of free memory in the compressed area is bigger than the
size of four zones, the compressed area is shrunk by deleting a
zone. If not, the system checks whether the size of the free memory is
smaller than the size of a zone; if so, a new zone is added to the
compressed area. As long as the size of free compressed memory is
between the size of a zone and four zones the compressed area size
remains the same; using this strategy we avoid resizing the compressed
area too often. The values of the shrink and grow threshold are
sensitive to the size of an application's working set: small
applications that execute on systems with small memories require small
threshold values (the compressed areas they require are small). For
the (large) applications we selected, we experimented with values of
the shrink threshold of three and four zones, and we found that the
performance improvements are the same. Furthermore, when the value of
the shrink threshold is bigger than the size of four zones, the degree
at which performance is improved decreases. The decrease in
performance is because the size of the compressed area found by the
adaptive scheme grows due to the increase in free compressed memory.
To assess the accuracy of our adaptation scheme, we examine the
performance of the qsim simulator and rand benchmark on a
system with fixed sizes of the compressed area and on an adaptive
compressed-memory system. We choose these two applications because
they have different memory access behavior, different compression
ratio, require large sizes of the compressed area, and finish
execution in a reasonable time. We run the experiments on the G5
machine that has a block size of 128 bytes and a zone size of 4 MB; the
value of the compression factor is 9 for qsim and 14 for
rand. The measurements for the qsim simulations and for the
rand benchmarks are summarized in Figure 4
and Figure 5, and show that the size found by our
resizing scheme is among those that improve performance the most.
Figure 4:
qsim execution time on an Apple G5 with 1 GB physical
memory for fixed sizes of the compressed area.
[Working set size 1.33 GB]
![\includegraphics[scale=0.4]{fix-133.eps}](img5.png) |
[Working set size 1.77 GB]
![\includegraphics[scale=0.4]{fix-177.eps}](img6.png) |
[Working set size 1.99 GB]
![\includegraphics[scale=0.4]{fix-199.eps}](img7.png) |
[Working set size 2.66 GB]
![\includegraphics[scale=0.4]{fix-266.eps}](img8.png) |
|
Figure 5:
rand execution time on an Apple G5 with 1 GB physical
memory for fixed sizes of the compressed area.
[Working set size 1.2 GB, 200,000 random
writes]![\includegraphics[scale=0.4]{fix-rand12.eps}](img9.png) |
[Working set size 1.4 GB, 1,200,000 random
writes]![\includegraphics[scale=0.4]{fix-rand14.eps}](img10.png) |
[Working set size 1.8 GB, 6,000,000 random
writes]![\includegraphics[scale=0.4]{fix-rand18.eps}](img11.png) |
|
To sum up, our design and adaptation scheme minimize the number of
resizing operations: the memory system usage is checked periodically
(and not at every access to the compressed data), the compressed area
is not resized every time the system usage is checked, and the
compressed area is grown and shrunk by adding and removing zones (and
not single pages).
System performance often depends upon more than one factor. In this
section we isolate the performance effects of each factor that
influence the compressed-memory overhead. We use the 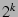 design to
determine the effect of k factors, each of which has two design
alternatives. We use the design to
determine the effect of k factors, each of which has two design
alternatives. We use the 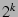 design because it is easy to analyze
and helps sorting out factors in the order of impact [9]. design because it is easy to analyze
and helps sorting out factors in the order of impact [9].
As previously described, the compressed area is based on zones that
are self contained consisting of all necessary overhead data
structures required to manage the compressed memory within a zone.
Because a zone uses the block table and comp page table to
manage its compressed data (see Figure 2), the
compressed-memory overhead is the sum of the sizes of these two data
structures:
 . (Because all zones are equal in size, all
block tables and comp page tables have the same size.)
Formally, the memory overhead is given by Eq. 1. (The
number of entries in the comp page table gives the maximum
number of compressed pages that can be stored within a zone, and can
be changed by changing the compression factor parameter.) . (Because all zones are equal in size, all
block tables and comp page tables have the same size.)
Formally, the memory overhead is given by Eq. 1. (The
number of entries in the comp page table gives the maximum
number of compressed pages that can be stored within a zone, and can
be changed by changing the compression factor parameter.)
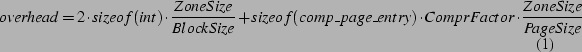
Eq. 1 shows that the three factors that affect the
compressed-memory overhead and need to be studied are the compression
factor (ComprFactor), block size (BlockSize), and zone
size (ZoneSize); the page size factor (PageSize) is fixed.
We use the 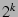 factorial design to determine the effect of the three
factors (k=3) on an application's execution time [9]. The
factors and their level assignments for the qsim simulations are
shown in Table 6. The factorial design to determine the effect of the three
factors (k=3) on an application's execution time [9]. The
factors and their level assignments for the qsim simulations are
shown in Table 6. The 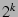 design and the measured
performance in design and the measured
performance in 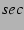 is shown in Table 7. We use the sign
table method to compute the portion of variation explained by the
three factors and their interaction, and we summarize the computations
in Table 8, column ``qsim simulations''. The
results show that most of the variation in the performance of the
qsim application is explained by the compression factor (column
``ComprFactor") and the interaction between the compression factor and
block size (column ``ComprFactor+BlockSize"). Moreover, for the large
simulations, the measurements indicate that a compressed-memory system
with a small zone size decreases the performance considerably (the
zone size explains more than 30% of the variation). We use the same is shown in Table 7. We use the sign
table method to compute the portion of variation explained by the
three factors and their interaction, and we summarize the computations
in Table 8, column ``qsim simulations''. The
results show that most of the variation in the performance of the
qsim application is explained by the compression factor (column
``ComprFactor") and the interaction between the compression factor and
block size (column ``ComprFactor+BlockSize"). Moreover, for the large
simulations, the measurements indicate that a compressed-memory system
with a small zone size decreases the performance considerably (the
zone size explains more than 30% of the variation). We use the same
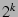 design to determine the effect of the three factors on
rand benchmark performance; the only difference is that the two
levels of the compression factor are 4 and 20. The measurements
summarized in Table 8, column ``rand benchmark'',
show again that the most important factors are the compression factor
(column ``ComprFactor") and the interaction between the compression
factor and block size (column ``ComprFactor+BlockSize"). The results
also show that large applications require large zone sizes. design to determine the effect of the three factors on
rand benchmark performance; the only difference is that the two
levels of the compression factor are 4 and 20. The measurements
summarized in Table 8, column ``rand benchmark'',
show again that the most important factors are the compression factor
(column ``ComprFactor") and the interaction between the compression
factor and block size (column ``ComprFactor+BlockSize"). The results
also show that large applications require large zone sizes.
Table 6:
Factors and levels.
| Factor |
Level -1 |
Level 1 |
| Compr factor |
4 |
14 |
| Block size |
64 B |
1024 B |
| Zone size |
2 MB |
8 MB |
|
Table 7:
Results of the 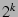 experiment. The performance of different
qsim simulations is measured in sec on an Apple G5 with
1 GB physical memory. experiment. The performance of different
qsim simulations is measured in sec on an Apple G5 with
1 GB physical memory.
| |
Compr |
2 MB |
8 MB |
| Test |
factor |
64 B |
1024 B |
64 B |
1024 B |
| |
4 |
245.30 |
258.30 |
688.96 |
165.64 |
| 1.33 GB |
14 |
147.38 |
253.49 |
144.51 |
152.63 |
| |
4 |
2,229.04 |
1,796.98 |
2,803.01 |
552.47 |
| 1.77 GB |
14 |
595.96 |
1,980.51 |
551.54 |
660.04 |
| |
4 |
7,351.71 |
5,479.42 |
4,395.01 |
888.60 |
| 1.99 GB |
14 |
954.99 |
6,354.63 |
872.34 |
973.74 |
| |
4 |
7,721.11 |
6,340.01 |
3,688.07 |
1,055.76 |
| 2.66 GB |
14 |
1,116.68 |
7,380.94 |
981.45 |
1,092.29 |
|
Table 8:
The portion of variation explained by the three factors and their
interaction.
| |
qsim simulations |
rand benchmark |
| |
1.33 GB |
1.77 GB |
1.99 GB |
2.66 GB |
1.2 GB |
1.4 GB |
1.8 GB |
| ComprFactor |
23.61% |
27.91% |
18.50% |
13.13% |
33.34% |
17.58% |
6.01% |
| BlockSize |
8.51% |
3.06% |
0.00% |
1.08% |
24.75% |
7.46% |
5.84% |
| ZoneSize |
3.31% |
8.96% |
39.03% |
47.99% |
2.68% |
22.93% |
58.38% |
| ComprFactor+BlockSize |
21.14% |
37.69% |
27.29% |
20.90% |
28.66% |
36.56% |
10.42% |
| ComprFactor+ZoneSize |
11.2% |
1.04% |
1.00% |
1.62% |
1.20% |
3.21% |
5.25% |
| BlockSize+ZoneSize |
21.81% |
20.70% |
11.08% |
10.62% |
1.78% |
8.46% |
6.00% |
| ComprFactor+ |
|
|
|
|
|
|
|
| +Block+ZoneSize |
10.42% |
0.64% |
3.10% |
4.65% |
7.58% |
3.81% |
8.10% |
|
Figure 6:
The influence of the three factors on the qsim performance.
The simulations run on an Apple G5 with 1 GB physical memory.
[The compression factor influence.]![\includegraphics[scale=0.4]{cf.eps}](img15.png) |
[The block size influence.]![\includegraphics[scale=0.4]{blk.eps}](img16.png) |
[The zone size influence.]![\includegraphics[scale=0.4]{zone.eps}](img17.png) |
|
Figure 7:
The influence of the three factors on the size of the compressed
area. The simulations run on an Apple G5 with 1 GB physical memory.
[The compression factor influence.]![\includegraphics[scale=0.4]{cm-cf.eps}](img18.png) |
[The block size influence.]![\includegraphics[scale=0.4]{cm-blk.eps}](img19.png) |
[The zone size influence.]![\includegraphics[scale=0.4]{cm-zone.eps}](img20.png) |
|
Let us consider an application with a high compression ratio that
executes on a system with a small compression factor. Because the
number of entries in the comp page table is smaller than the
number of compressed pages that can be stored in a zone, some memory
remains unused. On the other hand, a high value of the compression
factor increases the size of the comp page table
unnecessarily. The measurements summarized in
Figure 6(a) show that a compressed-memory system
improves an application's performance when its compression factor is
equal to or bigger than an application's compression ratio.
Furthermore, the data in Figure 7(a) indicates that
when the compression factor is smaller than an application's
compression ratio, also the size of the compressed area is bigger than
that which would suffice if enough entries to address a zone's memory
were available.
The internal fragmentation of the compressed-memory system is the sum
of the unused space in the last block of each compressed page. Because
the percentage of unused memory in the last block increases when the
block size increases, the internal fragmentation increases as well.
The measurements summarized in Figure 6(b) show
that block sizes smaller than 512 bytes yield good performance
improvements, and a block size of 1024 bytes decreases the qsim
performance for all input sizes. The data in
Figure 7(b) indicate that also the size of the
compressed area is influenced by the degree of the internal
fragmentation.
The results in Figure 6(c) indicate that a zone
size of 4 MB improves qsim performance for the simulations that
allocate 1.33 GB and 1.77 GB, but zones larger than 4 MB are required for
the simulations with large data footprints (those that allocate 1.99 GB
and 2.66 GB). Moreover, the data in Figure 7 show that
when the compressed area is allocated in zones of big sizes, the
amount of compressed area grows slightly because of the zone
granularity.
To summarize, our analysis shows that a compressed-memory system that has
a high value of the compression factor will improve performance for a
wide range of applications (with different compression
ratio). Measurements indicate that block sizes smaller than 512 bytes
work well for the selected applications. Furthermore, as the size of
an application' working set increases, also the zone size should
increase for compression to show maximum performance improvements.
This paper describes a transparent and effective solution to the
problem of executing applications with large data sets when the size
of the physical memory is less than what is required to run the
application without thrashing. Without a compressed-memory level in
the memory hierarchy, such applications experience memory starvation.
We describe a practical design for an adaptive compressed-memory
system and demonstrate that it can be integrated into an existing
general-purpose operating system. The key idea is to keep compressed
pages in zones; zones impose some locality on the blocks of a
compressed page so that at a later time, the operating system is able
to reclaim a zone if it is advisable to shrink the size of the
compressed data.
We evaluated the effectiveness of our system on a range of benchmarks
and applications. For synthetic benchmarks and small applications we
observe a slowdown up to a factor of 3; further tuning may further
reduce this penalty. For realistic applications, we observe an
increase in performance by a factor of 1.3 to 55. The dramatic
improvements in performance are directly correlated to the memory
access patterns of each program. If the working set and memory
footprint are strongly correlated, our compression technique is more
effective because the effects of memory starvation are more critical
to the program's overall performance. If the working set is a small
subset of the memory footprint, memory compression improves
performance but since memory starvation imposes a smaller impact on
program execution, its benefit is seen only during those periods of
memory starvation. The main memory compression benefits are sustained
under complex workload conditions and memory pressure, and the
overheads are small.
Although the amount of main memory in a workstation has increased with
declining prices for semiconductor memories, application developers
have even more aggressively increased their demands. A
compressed-memory level is a beneficial addition to the classical
memory hierarchy of a modern operating system, and this addition can
be provided without significant effort. The compressed-memory level
exploits the tremendous advances in processor speed that have not been
matched by corresponding increases in disk performance. Therefore, if
access times to memory and disk continue to improve over the next
decade at the same rate as they did during the last decade (the likely
scenario), software-only compressed-memory systems are an attractive
approach to improve total system performance.
We thank Kai Nagel for an version of the qsim traffic simulator.
We appreciate feedback and comments by the reviewers.
This work was funded, in part, by the NCCR ``Mobile Information and
Communication Systems'', a research program of the Swiss National
Science Foundation, and by a gift from Intel's Microprocessor Research
Laboratory.
- 1
-
Bigphysarea.
https://www.polyware.nl/ middelink/En/
hob-v4l.html#bigphysarea.
- 2
-
RAM Doubler 8.
https://www.powerbookcentral.com/
features/ramdoubler.shtml.
- 3
-
A. Alameldeen and D. Wood.
Adaptive Cache Compression for High-Performance Processors.
In Proc. ISCA, pages 212-223, Munich, Germany, June 2004.
IEEE.
- 4
-
R. Cervera, T. Cortes, and Y. Becerra.
Improving Application Performance through Swap Compression.
In Proc. 1999 USENIX Tech. Conf.: FREENIX Track, pages
207-218, Monterey, CA, June 1999.
- 5
-
N. Cetin, A. Burri, and K. Nagel.
A Large-Scale Multi-Agent Traffic Microsimulation based on Queue
Model.
In STRC, Monte Verita, Switzerland, March 2003.
- 6
-
R. de Castro, A do Lago, and D. Da Silva.
Adaptive Compressed Caching: Design and Implementation.
In Proc. SBAC-PAD, pages 10-18, Sao Paulo, Brazil, Nov. 2003.
IEEE.
- 7
-
F. Douglis.
The Compression Cache: Using On-line Compression to Extend Physical
Memory.
In Proc. Winter USENIX Conference, pages 519-529, San Diego,
CA, Jan. 1993.
- 8
-
M. Gorman.
Understanding The Linux Virtual Memory Manager.
Master's thesis, University of Limerick, July 2003.
https://www.skynet.ie/ mel/projects/vm/.
- 9
-
R. Jain.
The Art of Computer Systems Performance Analysis: Techniques
for Experimental Design, Measurement, Simulation, and Modeling.
John Wiley and Sons, New York, April 1991.
- 10
-
S. Kaplan.
Compressed Caching and Modern Virtual Memory Simulation.
PhD thesis, The University of Texas at Austin, Dec. 1999.
- 11
-
M. Kjelso, M. Gooch, and S. Jones.
Design and Performance of a Main Memory Hardware Compressor.
In Proc. 22nd Euromicro Conf., pages 423-430. IEEE Computer
Society Press, Sept. 1996.
- 12
-
M. Kjelso, M. Gooch, and S. Jones.
Performance Evaluation of Computer Architectures with Main Memory
Data Compression.
Journal of Systems Architecture, 45:571-590, 1999.
- 13
-
A. Rubini and J. Corbet.
Linux Device Drivers.
O'Reilly, 2nd edition, June 2001.
- 14
-
V. Schuppan and A. Biere.
A Simple Verification of the Tree Identify Protocol with SMV.
In Proc. IEEE 1394 (FireWire) Workshop, pages 31-34, Berlin,
Germany, March 2001.
- 15
-
P. Wilson.
Operating System Support for Small Objects.
In Workshop on Object Orientation in Operating Systems, pages
80-86, Palo Alto, CA, Oct. 1991. IEEE.
- 16
-
P. Wilson, S. Kaplan, and Y. Smaragdakis.
The Case for Compressed Caching in Virtual Memory Systems.
In Proc. 1999 USENIX Tech. Conf., pages 101-116, Monterey, CA,
June 1999.
- 17
-
B. Yang, R. Bryant, D. O'Hallaron, A. Biere, O. Coudert, G. Janssen, R. Ranjan,
and F. Somenzi.
A Performance Study of BDD-Based Model Checking.
In FMCAD'98, pages 255-289, Palo Alto, CA, Nov. 1998.
Adaptive Main Memory Compression
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons camera3.tex
The translation was initiated by Irina Chihaia on 2005-02-18



Irina Chihaia
2005-02-18
|

![]() design to
determine the effect of k factors, each of which has two design
alternatives. We use the
design to
determine the effect of k factors, each of which has two design
alternatives. We use the ![]() design because it is easy to analyze
and helps sorting out factors in the order of impact [9].
design because it is easy to analyze
and helps sorting out factors in the order of impact [9].
![]() . (Because all zones are equal in size, all
block tables and comp page tables have the same size.)
Formally, the memory overhead is given by Eq. 1. (The
number of entries in the comp page table gives the maximum
number of compressed pages that can be stored within a zone, and can
be changed by changing the compression factor parameter.)
. (Because all zones are equal in size, all
block tables and comp page tables have the same size.)
Formally, the memory overhead is given by Eq. 1. (The
number of entries in the comp page table gives the maximum
number of compressed pages that can be stored within a zone, and can
be changed by changing the compression factor parameter.)
![]() factorial design to determine the effect of the three
factors (k=3) on an application's execution time [9]. The
factors and their level assignments for the qsim simulations are
shown in Table 6. The
factorial design to determine the effect of the three
factors (k=3) on an application's execution time [9]. The
factors and their level assignments for the qsim simulations are
shown in Table 6. The ![]() design and the measured
performance in
design and the measured
performance in ![]() is shown in Table 7. We use the sign
table method to compute the portion of variation explained by the
three factors and their interaction, and we summarize the computations
in Table 8, column ``qsim simulations''. The
results show that most of the variation in the performance of the
qsim application is explained by the compression factor (column
``ComprFactor") and the interaction between the compression factor and
block size (column ``ComprFactor+BlockSize"). Moreover, for the large
simulations, the measurements indicate that a compressed-memory system
with a small zone size decreases the performance considerably (the
zone size explains more than 30% of the variation). We use the same
is shown in Table 7. We use the sign
table method to compute the portion of variation explained by the
three factors and their interaction, and we summarize the computations
in Table 8, column ``qsim simulations''. The
results show that most of the variation in the performance of the
qsim application is explained by the compression factor (column
``ComprFactor") and the interaction between the compression factor and
block size (column ``ComprFactor+BlockSize"). Moreover, for the large
simulations, the measurements indicate that a compressed-memory system
with a small zone size decreases the performance considerably (the
zone size explains more than 30% of the variation). We use the same
![]() design to determine the effect of the three factors on
rand benchmark performance; the only difference is that the two
levels of the compression factor are 4 and 20. The measurements
summarized in Table 8, column ``rand benchmark'',
show again that the most important factors are the compression factor
(column ``ComprFactor") and the interaction between the compression
factor and block size (column ``ComprFactor+BlockSize"). The results
also show that large applications require large zone sizes.
design to determine the effect of the three factors on
rand benchmark performance; the only difference is that the two
levels of the compression factor are 4 and 20. The measurements
summarized in Table 8, column ``rand benchmark'',
show again that the most important factors are the compression factor
(column ``ComprFactor") and the interaction between the compression
factor and block size (column ``ComprFactor+BlockSize"). The results
also show that large applications require large zone sizes.