USENIX '05 Paper    [USENIX '05 Technical Program]

CHAMELEON: a self-evolving, fully-adaptive resource arbitrator for storage systems

Sandeep Uttamchandani$^{\dag}$ Li Yin$^{\ddag}$ Guillermo A. Alvarez$^{\dag}$ John Palmer$^{\ast}$ Gul Agha

$^{\dag}$ IBM Almaden Research Center

$^{\ddag}$ University of California, Berkeley

$^{\ast}$ University of Illinois at Urbana-Champaign

sandeepu@us.ibm.com, yinli@eecs.berkeley.edu, {alvarezg,jdp}@us.ibm.com, agha@cs.uiuc.edu

Abstract

Enterprise applications typically depend on guaranteed performance from the storage subsystem, lest they fail. However, unregulated competition is unlikely to result in a fair, predictable apportioning of resources. Given that widespread access protocols and scheduling policies are largely best-effort, the problem of providing performance guarantees on a shared system is a very difficult one. Clients typically lack accurate information on the storage system's capabilities and on the access patterns of the workloads using it, thereby compounding the problem. CHAMELEON is an adaptive arbitrator for shared storage resources; it relies on a combination of self-refining models and constrained optimization to provide performance guarantees to clients. This process depends on minimal information from clients, and is fully adaptive; decisions are based on device and workload models automatically inferred, and continuously refined, at run-time. Corrective actions taken by CHAMELEON are only as radical as warranted by the current degree of knowledge about the system's behavior. In our experiments on a real storage system CHAMELEON identified, analyzed, and corrected performance violations in 3-14 minutes--which compares very favorably with the time a human administrator would have needed. Our learning-based paradigm is a most promising way of deploying large-scale storage systems that service variable workloads on an ever-changing mix of device types.

1 Introduction

A typical consolidated storage system at the multi-petabyte level serves the needs of independent, paying customers (e.g., a storage service provider) or divisions within the same organization (e.g., a corporate data center). Consolidation has proven to be an effective remedy for the low utilizations that plague storage systems [10], for the expense of employing scarce system administrators, and for the dispersion of related data into unconnected islands of storage. However, the ensuing resource contention makes it more difficult to guarantee a portion of the shared resources to each client, regardless of whether other clients over- or under-utilize their allocations--guarantees required by the prevalent utility model.

This paper addresses the problem of allocating resources in a fully automated, cost-efficient way so that most clients experience predictable performance in their accesses to a shared, large-scale storage utility. Hardware costs play a dwindling role relative to managing costs in current enterprise systems [10]. Static provisioning approaches are far from optimal, given the high burstiness of I/O workloads and the inadequate available knowledge about storage device capabilities. Furthermore, efficient static allocations do not contemplate hardware failures, load surges, and workload variations; system administrators must currently deal with those by hand, as part of a slow and error-prone observe-act-analyze loop. Prevalent access protocols (e.g., SCSI and FibreChannel) and resource scheduling policies are largely best-effort; unregulated competition is unlikely to result in a fair, predictable resource allocation.

Previous work on this problem includes management policies encoded as sets of rules [13,27], heuristic-based scheduling of individual I/Os [7,12,15,19], decisions based purely on feedback loops [17,18] and on the predictions of models for system components [1,2,3]. The resulting solutions are either not adaptive at all (as in the case of rules), or dependent on models that are costly to develop, or ignorant of the system's performance characteristics as observed during its lifetime.

This paper's main contribution is a novel technique for providing performance guarantees in shared storage systems, based on a combination of performance models, constrained optimization, and incremental feedback. CHAMELEON is a framework in which clients whose negotiated Service Level Agreement (SLAs) are not being met get access to additional resources freed up by throttling (i.e., rate-limiting) [7,17] competing clients. Our goal is to make more accurate throttling decisions as we learn more about the characteristics of the running system, and of the workloads being presented to it. As shown in Figure 1, CHAMELEON operates at any point in a continuum between decisions made based on relatively uninformed, deployment-independent heuristics on the one hand, and blind obedience to models of the particular system being managed on the other hand.

Figure 1: CHAMELEON moves along the line according to the quality of the predictions generated by the internally-built models at each point in time.

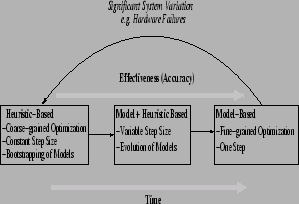CHAMELEON can react to workload changes in a nimble manner, resulting in a marginal number of quality of service (QoS) violations. In our experiments on a real storage system using real-world workload traces, CHAMELEON managed to find the set of throttling decisions that yielded the maximum value of the optimization function, while minimizing the amount of throttling required to meet the targets and while maximizing the number of clients whose QoS requirements are satisfied. Since our approach does not depend on pre-existing device or workload models, it can be easily deployed on heterogeneous, large-scale storage systems about which little is known. Our ultimate vision, of which CHAMELEON is just a part, is to apply a variety of corrective actions to solve a variety of systems management problems while operating on incomplete information [25].

Section 2 presents the architecture of CHAMELEON. We then proceed to describe the main components: the models (Section 3), the reasoning engine (Section 4), the base heuristics (Section 5), and the feedback-based throttling executor (Section 6). Section 7 describes our prototype and experimental results. Section 8 reviews previous research in the field; we conclude in Section 9.

2 Overview of CHAMELEON

CHAMELEON is a framework for providing predictable performance to multiple clients accessing a common storage infrastructure, as shown in Figure 2. Multiple hosts connect to storage devices in the back end via interconnection fabrics. CHAMELEON can monitor, and optionally delay, every I/O processed by the system; this can be implemented at each host (as in our prototype), or at logical volume managers, or at block-level virtualization appliances [9]. Each workload $j$ has a known SLA$_j$ associated with it, and uses a fixed set of components--its invocation path--such as controllers, logical volumes, switches, and logical units (LUNs). When SLAs are not being met, CHAMELEON identifies and throttles workloads; when it detects unused bandwidth, it unthrottles some of the previously-throttled workloads.

Our SLAs are conditional: a workload will be guaranteed a specified upper bound on average I/O latency, as long as its I/O rate (i.e., the throughput) is below a specified limit. An SLA is violated if the rate is below the limit, but latency exceeds its upper bound. If workloads exceed their stated limits on throughput, the system is under no obligation of guaranteeing any latency. Obviously, such rogue workloads are prime candidates for throttling; but in some extreme cases, well-behaved workloads may also need to be restricted. CHAMELEON periodically evaluates the SLAs, i.e., the average latency and throughput value of each workload; depending on how much the workload is being throttled, it receives tokens (one per I/O) for flow control using a leaky bucket protocol [24]. The periodic interval for SLA evaluation has to be large enough to smooth out bursty intervals, and small enough for the system to be reasonably responsive; we empirically set this interval to 60 s. in our prototype implementation.

Figure 2: System model.

Figure 3: Architecture of CHAMELEON.

The core of CHAMELEON consists of four parts, as shown in Figure 3:

• Knowledge base: by taking periodic performance samples on the running system, CHAMELEON builds internal black-box models of system behavior without any human supervision. Models get better as time goes by, for CHAMELEON refines them automatically.

• Reasoning engine: CHAMELEON employs optimization techniques, informed by the black-box models. It computes throttle values, and quantifies the statistical confidence of its own decisions.

• Designer-defined policies: As a fallback mechanism, we maintain a set of fixed heuristics specified by the system designer for system-independent, coarse-grained resource arbitration.

• Informed feedback module: The general guiding principle is to take radical corrective action as long as that is warranted by the available knowledge about the system. If the confidence value from the solver is below a certain threshold (e.g., during bootstrapping of the models), CHAMELEON falls back on the fixed policies to make decisions.

3 Knowledge base

CHAMELEON builds models in an automatic, unsupervised way. It uses them to characterize the capabilities of components of the storage system, the workload being presented to them, and its expected response to different levels of throttling.

Models based on simulation or emulation require a fairly detailed knowledge of the system's internals; analytical models require less, but device-specific optimizations must still be taken into account to obtain accurate predictions [26]. Black-box models are built by recording and correlating inputs and outputs to the system in diverse states, without regarding its internal structure. We chose them because of properties not provided by the other modeling approaches: black-box models make very few assumptions about the phenomena being modeled, and can readily evolve when it changes. Because of this, they are an ideal building block for an adaptive, deployment-independent management framework that doesn't depend on preexisting model libraries.

At the same time, the black-box models used in CHAMELEON are less accurate than their analytical counterparts; our adaptive feedback loop compensates for that. The focus of this paper is to demonstrate how several building blocks can work together in a hybrid management paradigm; we do not intend to construct good models, but to show that simple modeling techniques are adequate for the problem. CHAMELEON's models are constructed using Support Vector Machines (SVM) [16], a machine-learning technique for regression. This is similar to the CART [29] techniques for modeling storage device performance, where the response of the system is measured in different system states and represented as a best-fit curve function. Table-based models [2], where system states are exhaustively recorded in a table and used for interpolation, are not a viable solution as they represent the model as a very large lookup table instead of the analytic expressions that our constraint solver takes as input.

Black-box models depend on collecting extensive amounts of performance samples. Some of those metrics can be monitored from client hosts, while others are tallied by each component--and collected via proprietary interfaces for data collection, or via standard protocols such as SMI-S [20].

A key challenge is bootstrapping, i.e., how to make decisions when models have not yet been refined. There are several solutions for this: run a battery of tests in non-production mode to generate baseline models, or run in a monitor-only mode until models are sufficiently refined, or start from a pre-packaged library (e.g., a convenient oversimplification such as an M/M/1 queueing system.) We follow different approaches for different model types.

3.1 Component models

Figure 4: Component model.

A component model predicts values of a delivery metric as a function of workload characteristics. CHAMELEON can in principle accommodate models for any system component. In particular, the model for the response time of a storage device $i$ takes the form: c$_i$(req_size, req_rate, rw_ratio, random/sequential, cache_hit_rate). Function $c_i$ is inherently non-linear, but can be approximated as piecewise linear with a few regions; a projection of a sample $c_i$ is shown in Figure 4. Another source of error is the effect of multiple workloads sending interleaved requests to the same component. We approximate this nontrivial computation by estimating the wait time for each individual stream as in a multi-class queueing model [14]; more precise solutions [5] incorporate additional workload characteristics. The effects of caching at multiple levels (e.g., hosts, virtualization engines, disk array controllers, disks) also amplify errors.

We took the liberty of bootstrapping component models by running off-line calibration tests against the component in question: a single, unchanging, synthetic I/O stream at a time, as part of a coarse traversal of $c_i$'s parameter space.

3.2 Workload models

Representation and creation of workload models has been an active area of research [6]. In CHAMELEON, workload models predict the load on each component as a function of the request rate that each workload injects into the system. For example, we denote the predicted rate of requests at component $i$ originated by workload $j$ as w$_{i,j}$(workload_request_rate$_j$). In real scenarios, function $w_{i,j}$ changes continuously as workload $j$ changes or other workloads change their access patterns (e.g., a workload with good temporal locality will push other workloads off the cache). To account for these effects, we represent function $w_{i,j}$ as a moving average [23] that gets recomputed by SVM every $n$ sampling periods.

Figure 5: Workload model for SPC.

Figure 5 shows the workload models for the SPC web-search trace [21] accessing a 24-drive RAID 1 LUN on an IBM FAStT 900 storage controller. From the graph, a workload request rate of 1500 IOPS in SPC translates to 2000 IOPS at the controller.

In practical systems, reliable workload data can only be gathered from production runs. We therefore bootstrap workload models by collecting performance observations; CHAMELEON resorts to throttling heuristics in the meantime, until workload models become accurate enough.

3.3 Action models

In general, action models predict the effect of corrective actions on workload requirements. The throttling action model computes each workload's average request rate as a function of the token issue rate, i.e., a$_j$(token_issue_rate$_j$). Real workloads exhibit significant variations in their I/O request rates due to burstiness and to ON/OFF behaviors [5]. We model $a$ as a linear function: $a_j(token\_issue\_rate_j) = \theta \times token\_issue\_rate_j$ where $\theta = 1$ initially for bootstrapping. This simple model assumes that the components in the workload's invocation path are not saturated.

Function $a_j$ will, in general, also deviate from our linear model because of performance-aware applications (that modify their access patterns depending on the I/O performance they experience) and of higher-level dependencies between applications that magnify the impact of throttling.

4 Reasoning engine

The reasoning engine computes the rate at which each workload stream should be allowed to issue I/Os to the storage system. It is implemented as a constraint solver (using piecewise-linear programming [8]) that analyzes all possible combinations of workload token rates and selects the one that optimizes an administrator-defined objective function, e.g., ``minimize the number of workloads violating their SLA'', or ``ensure that highest priority workloads always meet their guarantees''. Based on the errors associated with the models, the output of the constraint solver is assigned a confidence value.

It should be noted that the reasoning engine is not just invoked upon an SLA violation to decide throttle values, but also periodically to unthrottle the workloads if the load on the system is reduced.

4.1 Intuition

Figure 6: Overview of constrained optimization.

The reasoning engine relies on the component, workload, and action models as oracles on which to base its decision-making. Figure 6 illustrates a simplified version of how the constraint solver builds a candidate solution: 1) for each component used by the underperforming workload (i.e., the one not meeting its SLA), use the component's model to determine the change in request rate at the component required to achieve the needed decrease in component latency; 2) query the model for each workload using that components, to determine which change in the workload's I/O injection rate is needed to relieve the component's load; 3) using the action model, determine the change in the token issue rate needed for the sought change in injection rate; 4) record the value of the objective function for the candidate solution. Then repeat recursively for all combinations of component, victim workload, and token issue rates. The reasoning engine is actually more general: it considers all solutions, including the ones in which the desired effect is achieved by the combined results of throttling more than one workload.

4.2 Formalization in CHAMELEON

We formulate the task of computing throttle values in terms of variables, objective function, and constraints as follows.

Variables: One per workload, representing its token issue rate: $t_{1}, t_{2}, \ldots$

Objective function: Workloads are pigeonholed into one of four regions as in Figure 7, according to their current request rate, latency, and SLA goals. Region names are mostly self-explanatory--lucky workloads are getting a higher throughput while meeting the latency goal, and exceeded workloads get higher throughput at the expense of high latency.

Figure 7: Workload classification. Region limits correspond to the 100% of the SLA values.

Many objective functions can be accommodated by the current CHAMELEON prototype (e.g., all linear functions); moreover, it is possible to switch them on the fly. For our experiments, we minimized

$$\sum_{i \not\in {\tt failed}} \left\vert P_{quad_i}P_{Wi} \frac{SLA_{Wi} - a_{i}(t_{i})}{SLA_{W_{i}}}\right\vert$$

where $P_{Wi}$ are the workload priorities, $P_{quad_i}$ are the quadrant priorities (i.e., the probability that workloads in each region will be selected as throttling candidates), and $a_i(t_{i})$ represents the action model for $Wi$. Table 1 provides some insight into this particular choice.

Table 1: Internals of the objective function.

Intuition	How it is captured
The lower a workload's priority, the higher its probability of being throttled	The solver minimizes the objective function; violating the SLA of a higher priority workload will reflect as a higher value for $P_{Wi} \frac{SLA_{Wi} - a_{i}(t_{i})}{SLA_{W_{i}}}$
Workloads in the lucky or exceeded region have a higher probability of being throttled	This is ensured by the $P_{quad_i}$ variable in the objective function; it has higher values for lucky and exceeded (e.g., $P_{meet} = 1, P_{exceed} = 8, P_{lucky} =32$). It is also possible to define $P_{quad_i}$ as a function.
Workloads should operate close to the SLA boundary	By definition of the objective function; it is also possible to add a bimodal function, to penalize workloads operating beyond their SLA.

Constraints: Constraints are represented as inequalities: the latency of a workload should be less than or equal to the value specified in the SLA. More precisely, we are only interested in solutions that satisfy $latency_{W_j} \leq SLA_{W_j}$ for all workloads $W_j$ running in the system. We estimate the contribution of component $i$ to the latency of $W_j$ by composing our models in the knowledge base, i.e., $latency_{i,j}= c_i(w_{i,j}(a_j(t_j)))$.

For example, the latency constraint for a single workload $W_1$ running in the system with its I/O requests being served by a storage controller followed by physical disks is

$$\begin{eqnarray*} c_{controller}(w_{controller,1}(a_{1}(t_1))) & & \\ +c_{disks}(w_{disks,1}(a_{1}(t_1))) & \leq & SLA_{1} \end{eqnarray*}$$

In a more general example, workloads $W_{1}, W_{5}$ share the storage controller:

$$\begin{eqnarray*} total\_req_{controller} & = & w_{controller,1}(a_{1}(t_1)) \... ... & w_{disks,1}(a_{1}(t_1)) \\ & & + w_{disks,5}(a_{5}(t_5)); \end{eqnarray*}$$

$$\begin{eqnarray*} c_{controller}(total\_req_{controller}) & & \\ +c_{disks}(total\_req_{disks}) & \leq & SLA_1 \end{eqnarray*}$$

4.3 Workload unthrottling

CHAMELEON invokes the reasoning engine periodically, to re-assess token issue rates; if the load on the system has decreased since the last invocation, some workloads may be unthrottled to re-distribute the unused resources based on workload priorities and average I/O rates. If a workload is consistently wasting tokens issued for it (because it has less significant needs), unused tokens will be considered for re-distribution; on the other hand, if the workload is using all its tokens, they won't be taken away from it, no matter how low its priority is. CHAMELEON makes unthrottling decisions using the same objective function with additional ``lower-bound'' constraints such as not allowing any I/O rate to become lower than its current average value.

4.4 Confidence on decisions

There are multiple ways of capturing statistical confidence values [14]. CHAMELEON uses the following formula to capture both the errors from regression and from residuals (i.e., models being used on inputs where they were not trained):

$$S_{p}\; = S \sqrt{1 + \frac{1}{n} + \frac{(x_{p} - \overline{x})^2}{\sum x^2 - n\overline{x}^2}}$$

where $S$ is the standard error, $n$ is the number of points used for regression, and $\overline{x}$ is the mean value of the predictor variables used for regression. $S_{p}$ represents the standard deviation of the predicted value $y_{p}$ using input variable $x_{p}$. In CHAMELEON, we represent the confidence value $CV$ of a model as the inverse of its $S_{p}$, and we define the overall confidence on the reasoning engine's decisions as $CV_{component} \times CV_{workload} \times CV_{action}$.

5 Designer-defined policies

The system designer defines heuristics for coarse-grained throttling control. Heuristics are used to make decisions whenever the predictions of the models cannot be relied upon--either during bootstrapping or after significant system changes such as hardware failures. Sample heuristics include ``if system utilization is greater than 85%, start throttling workloads in the lucky region'', or ``if the workload-priority variance is less than 10%, uniformly throttle all workloads sharing the component''.

These heuristics can be expressed in a variety of ways such as Event-Condition-Action (ECA) rules or hard-wired code. In any case, fully specifying corrective actions at design time is an error-prone solution to a highly complex problem [25], especially if they are to cover a useful fraction of the solution space and to accommodate priorities. It is also very hard to determine accurate threshold values to differentiate different scenarios, in the absence of any solid quantitative information about the system being built. In CHAMELEON, the designer-defined heuristics are implemented as simple hard-wired code which is a modified version of the throttling algorithm used in Sleds [7]:

1. Determine the $compList$ of components being used by the underperforming workload.

2. For each component in the $compList$, add the non-underperforming workloads using it to the $candidateList$.

3. Sort the $candidateList$ first by current operating quadrant: lucky first, then exceed, then meet. Within each quadrant, sort by workload priority.

4. Traverse the $candidateList$ and throttle each workload, either uniformly or proportionally to its priority (the higher the priority, the less significant the throttling).

6 Informed feedback module

The feedback module (Figure 8) incrementally throttles workloads based on the decisions of either the reasoning engine or the system-designer heuristics. If CHAMELEON is following the reasoning engine, throttling is applied at incremental steps whose size is proportional to the confidence value of the constraint solver; otherwise, the throttling step is a small constant value.

After every $m$ throttling steps, the feedback module analyzes the state of the system. If any of the following conditions is true, it re-invokes the reasoning engine; otherwise it continues applying the same throttling decisions in incremental steps:

• Latency increases for the underperforming workload (i.e., it moves away from the meet region).
• A non-underperforming workload moves from meet or exceed to lucky.
• Any workload undergoes a 2X or greater variation in the request rate or any other access characteristic, compared to the values at the beginning of throttling.
• There is a 2X or greater difference between predicted and observed response times for a component.

Figure 8: Operation of the feedback module.

7 Experimental evaluation

The experimental setup consists of a host machine generating multiple I/O streams on a shared storage infrastructure. The host is an IBM x-series 440 server (2.4GHz 4-way Intel Pentium 4 with 4GB RAM running Redhat Server Linux, 2.1 kernel); the back-end storage is a 24-drive RAID 1 LUN created on a IBM FAStT 900 storage controller with 512MB of on-board NVRAM, and accessed as a raw device so that there is no I/O caching at the host. The host and the storage controller are connected using a 2Gbps FibreChannel (FC) link.

The key capability of CHAMELEON is to regulate resource load so that SLAs are achieved. The experimental results use numerous combinations of synthetic and real-world request streams to evaluate the effectiveness of CHAMELEON. As expected, synthetic workloads are easier to handle compared to their real-world counterparts that exhibit burstiness and highly variable access characteristics.

7.1 Using synthetic workloads

The synthetic workload specifications used in this section were derived from a study done in the context of the Minerva project [1]. Since the workloads are relatively static and controlled, our action and workload models have small errors as quantified by the correlation coefficient $r$ [14]. In general, the closer $r$ is to 1, the more accurate the models are; in this experiment, the component model has $r=0.72$, and the workload and action models have $r > 0.9$.

These tests serve two objectives. First, they evaluate the correctness of the decisions made by the constraint solver. Throttling decisions should take into account each workload's priority, its current operating point compared to the SLA, and the percentage of load on the components generated by the workload. Second, these tests quantify the effect of model errors on the output values of the constraint solver and how incremental feedback helps the system converge to an optimal state.

Table 2: Synthetic workload streams.

Workload	Request size [KB]	Rd/wrt ratio	Seq/rnd ratio	Foot-print [GB]
$W_1$	27.6	0.98	0.577	30
$W_2$	2	0.66	0.01	60
$W_3$	14.8	0.641	0.021	50
$W_4$	20	0.642	0.026	60

We report experimental results by showing each workload's original and new (i.e., post-throttling) position in the classification chart, as defined in Figure 7.

Case 1: Effect of workload and quadrant priorities

Figure 9 compares the direct output of the constraint solver with priority values for the workloads ( $W_{1}= 8, W_{2}=8, W_{3}=2, W_{4}= 8$) and the SLA quadrant priorities (failed = 16, meet = 2, exceed=8 , lucky=8). In comparison to the no priority scenario, $W_{3}$ and $W_{2}$ are throttled more when priorities are assigned for the workloads and quadrants respectively. This is because the constraint solver optimizes the objective function by throttling the lower priority workloads more aggressively before moving on to the higher priority ones.

Figure 9: Effect of priority values on the output of the constraint solver.

Case 2: Usage of the component by the workload

This test is a sanity check with workload $W_{5}$ operating primarily from the controller cache (2KB sequential read requests). Because $W_5$ does not consume disk bandwidth, the reasoning engine should not attempt to solve solve the SLA violation for $W_{1}$ by throttling $W_{5}$ even if $W_{5}$ has the lowest priority. As shown in Figure 10, the reasoning engine selects $W_{2}$ and $W_{3}$.

Figure 10: Sanity test for the reasoning engine (workload $W_5$ operating from controller cache.)

7.2 Replaying real-world traces

For these experiments, we replay the web-search SPC trace [21] and HP's Cello96 trace [11]. Both are block-level traces with timestamps recorded for each I/O request. We use approximately 6 hours of SPC and one day of Cello96. To generate a reasonable I/O load for the storage infrastructure, SPC was replayed 40 times faster and Cello96 was replayed 10 times faster.

In addition to the traces, we used a phased, synthetic workload was used; this workload was assigned the highest priority. In an uncontrolled case i.e. without throttling, with three workloads running on the system, one or more of them violate their SLA. Figure 11 shows the throughput and latency values for uncontrolled case. For all the figures in this subsection, there are four parts (ordered vertically): the first plot represents the throughput for the SPC, Cello96, and the synthetic workload. The second, third, and fourth plots represent the latency for each of these workloads respectively.

Figure 11: Uncontrolled throughput and latency values for real-world workload traces.

The aim of the tests is to evaluate the following:

• The throttling decisions made by CHAMELEON for converging the workloads towards their SLA.
• The reactiveness of the system with throttling and periodic unthrottling of workloads (under reduced system load).
• The handling of unpredictable variations in the system that cause errors in the model predictions, forcing CHAMELEON to use the sub-optimal but conservative designer-defined policies.

For these experiments, the models were reasonably accurate (component $r=0.68$, workload $r=0.7$, and action $r= 0.6$).In addition, the SLAs for each workload are: Cello96 1000 IOPS with 8.2ms latency, SPC 1500 IOPS with 6.5 ms latency and 1600 IOPS with 8.6ms latency for the synthetic workload unless otherwise specified.

Case 1: Solving SLA violations using throttling

The behavior of the system is shown in figure 12. To explain the working of CHAMELEON, we divide the time-series into phases (shown as dotted vertical line in the figures) described as follows:

Figure 12: Throughput and latency values for real-world workload traces with throttling (without periodic unthrottling.)

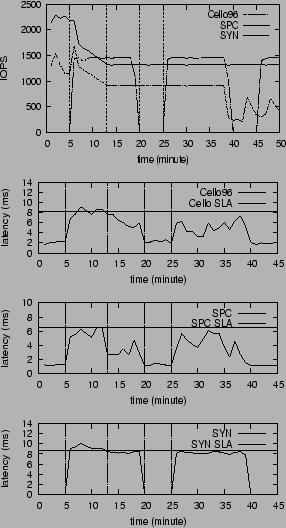Phase 0 (t=0 to t=5 min): Only the SPC and Cello96 traces are running on the system; the latency values of both these workloads are significantly below the SLA.

Phase 1 (t= 5 min to t= 13 min): The phased synthetic workload is introduced in the system. This causes an SLA violation for the Cello96 and synthetic traces. CHAMELEON triggers the throttling of the SPC and Cello96 workloads (Cello96 is also throttled because it is operating in the exceeded region, means it is sending more than it should. Therefore, it is throttled even if its SLA latency goal is not met.) The system uses a feedback approach to move along the direction of the output of the constraint solver. In this experiment, the feedback system starts from 30% of the throttling value and uses step size is 8% (30% and 8% are decided according to the confidence value of the models). It took the system 6 minutes to meet the SLA goal and stop the feedback.

Phase 2 (t=13 min to t= 20 min ): The system stabilizes after the throttling and all workloads can meet their SLAs.

Phase 3 (t=20 min to t= 25 min ): The synthetic workload enters the OFF phase. During this time, the load on the system is reduced, but the throughput of Cello96 and SPC remains the same.

Phase 4 ( beyond t= 25 min): The system is stable, with all the workloads meeting their SLAs. As a side note, around t=39 min the throughput of Cello96 decreases further; this is because of characteristics of the trace.

Figure 12 shows the effectiveness of the throttling: all workloads can meet their SLA after throttling. However, because the lack of an unthrottling scheme, throttled workloads have no means to increase their throughput even when tokens are released by other workloads. Therefore, the system is underutilized.

Case 2: Side-by-side throttling and unthrottling of workloads

The previous experiment demonstrates the effectiveness of throttling. Figure 13 shows throttling combined with unthrottling of workloads during reduced system load. Compared to Figure 12, the key differences are: 1) SPC and Cello96 increase their request-rate when the system load is reduced (t=17min to t=27 min), improving overall system utilization; 2) the system has a non-zero settling time when the synthetic workload is turned on (t=27 min to t=29 min). In summary, unthrottling allows for better system utilization, but requires a non-zero settling time for recovering the resources.

Figure 13: Throughput and latency values for real-world workload traces with throttling and periodic unthrottling.

Case 3: Handling changes in the confidence value of models at run-time

This test demonstrates how CHAMELEON handles changes in the confidence values of the models at run-time; these changes can be due to unpredictable system variations (hardware failures) or un-modeled properties of the system (such as changes in the workload access characteristics that change the workload models). It should be noted that refining the models to reflect the changes will not be instantaneous; in the meantime, CHAMELEON should have the ability to detect decreases in the confidence value and switch to a conservative management mode (e.g., using designer-defined policies, or generate a warning for a human administrator).

Figure 14 show the reaction of the system when the access characteristics of the SPC and Cello96 workloads are synthetically changed such that the cache hit rate of Cello96 increases significantly (in reality, a similar scenario arise due to changes in the cache allocation to individual workload streams sharing the controller) and the SPC is doing more random access (sequential random ratio increases from 0.11 to 0.5). In the future, we plan to run experiments with hardware failures induced on the RAID 1 logical volume.

The SLAs used for this test are: Cello96 has a SLA with 1000 IOPS with 7ms latency, SPC is 2000 IOPS with 8.8ms latency and the synthetic workloads has a SLA with 1500 IOPS and 9ms latency.

Figure 14: Handling a change in the confidence value of the models at run-time.

Phase 0 (at t= 3 mins): The synthetic workload violates its latency SLA. In response, CHAMELEON decides to throttle the Cello96 workload (using the original workload model). The output of the reasoning engine as a confidence value of 65%

Phase 1 (t= 3 min to t = 13 min): The feedback module continues to throttle for 3 consecutive increments; since the latency of the synthetic workload does not change, it re-invokes the reasoning engine. The output of the reasoning engine is similar to the previous invocation (since the models haven`t changed), but its confidence value is lower (because of the higher differences between predicted and observed model values). This repeats for consecutive invocations of the reasoning engine after which the feedback module switches to use the designer-defined policies.

Phase 2 (t= 13 min to t=17 min): A simple designer policy the CHAMELEON uses is to throttle all the non-violating workloads uniformly (uniform pruning). Both SPC and Cello96 are throttled in small steps (5% of their SLA IOPS) till the latency SLA of the synthetic workload is satisfied.

Phase 3 (beyond t= 17min): All workloads are meeting their SLA goals and the system is stabilized.

8 Related work

Most storage management frameworks (including all commercial tools, e.g., BMC Patrol [4]) encode policies as ECA rules [27,13] that fire when some precondition is satisfied--typically, when one or more system metrics cross predetermined thresholds. Rules are a clumsy, error-prone programming language; they front-load all the complexity into the work of creating them at design time, in exchange for simplicity of execution at run time. Administrators are expected to account for all relevant system states, to know which corrective action to take in each case, to specify useful values for all the thresholds that determine when rules will fire, and to make sure that the right rule will fire if preconditions overlap. Moreover, simple policy changes can translate into modifications to a large number of rules. Rule-based systems are only as good as the human who wrote the rules; they can just provide a coarse level of control over the system. Some variations rely on case-based reasoning [28] to iteratively refine rules from a tabula rasa initial knowledge base. This approach does not scale well to real systems, because of the exponential size of the search space that is explored in an unstructured way. In contrast, CHAMELEON relies on constrained optimization to steer the search in the full space of throttle values, and uses its dynamically refined models in lieu of fixed thresholds.

Feedback-based approaches use a narrow window of the most recent performance samples to make allocation decisions based on the difference between the current and desired system states. They are not well-suited for decision-making with multiple variables [22], and can oscillate between local optima. Façade [19] controls the queue length at a single storage device; decreasing the queue length is equivalent to throttling the combination of all workloads, instead of (as in CHAMELEON) selectively throttling only the workloads that will minimize the objective function. Triage [17] keeps track of which performance band the system is operating in; it shares Façade's lack of selectivity, as a single QoS violation may bring the whole system down to a lower band (which is equivalent to throttling every workload). Sleds [7] can selectively throttle just the workloads supposedly responsible for the QoS violations, and has a decentralized architecture that scales better than Façade's. However, its policies for deciding which workload to throttle are hard-wired and will not adapt to changing conditions. Hippodrome [3] iteratively refines the data placement; each of its data migrations can take hours. It is a solution to longer-term problems than CHAMELEON, that is more appropriate for reacting in minutes to problems requiring immediate attention. Hippodrome can take a long time to converge (due to the high cost of migrating data) and can get stuck in local minima, for it relies on a variation of hill-climbing.

Scheduling-based approaches establish relative priorities between workloads and individual I/Os. Jin et al. [15] compared different scheduling algorithms for performance isolation and resource-usage efficiency; they found that scheduling is effective but cannot ensure tight bounds on the SLA constraints (essential for high-priority workloads). Stonehenge [12] uses a learning-based bandwidth allocation mechanism to map SLAs to virtual device shares dynamically; although it allows more general SLAs than CHAMELEON, it can only arbitrate accesses to the storage device, not to any other bottleneck component in the system. In general, scheduling approaches are designed to work well for the common case, not being effective in handling exception scenarios such as hardware failures.

Model-based approaches make decisions based on accurate models of the storage system. The main challenge is to build them, far from trivial in practical systems; system administrators very rarely have that level of information about the devices they use. Minerva [1] assumes that such models are given. CHAMELEON and Polus [25] (an extension of this vision) build those models on the fly, without supervision.

9 Conclusions

An ideal solution for resource arbitration in shared storage systems would adapt to changing workloads, client requirements and system conditions. It would also relieve system administrators from the burden of having to specify when to step in and take corrective action, and what actions to take--thus allowing them to concentrate on specifying the global objectives that maximize the storage utility's business benefit, and having the system take care of the details. No existing solution satisfies these criteria; prior approaches are either inflexible, or require administrators to supply up-front knowledge that is not available to them.

Our approach to identifying which client workloads should be throttled is based on constrained optimization. Constraints are derived from the running system, by monitoring its delivered performance as a function of the demands placed on it during normal operation. The objective function being optimized can be defined, and changed, by the administrator as a function of organizational goals. Given that the actions prescribed by our reasoning engine are only as good as the quality of the models used to compute them, CHAMELEON will switch to a conservative decision-making process if insufficient knowledge is available. CHAMELEON's approach to model building requires no prior knowledge about the quantitative characteristics of workloads and devices--and makes good decisions in realistic scenarios like those involving workloads with relative priorities. We replayed traces from production environments on a real storage system, and found that CHAMELEON makes very accurate decisions for the workloads examined. CHAMELEON always made the optimal throttling decisions, given the available knowledge. The times to react to and solve performance problems were in the 3-14 min. range, which is quite encouraging.

Areas for future work include component and workload models that incorporate additional relevant parameters, more general (non-linear) optimizers to accommodate the resulting, more accurate problem formulations, and even some degree of workload prediction using techniques related to ARIMA [23].

Acknowledgments: We wish to thank Randy Katz, Jai Menon, Kaladhar Voruganti and Honesty Young for their inputs on the direction of this work and valuable comments on earlier versions of this paper. We also thank Lucy Cherkasova for her excellent shepherding. Finally, we thank the HP Labs Storage Systems Department for making their traces available to the general public.

Bibliography

1

Guillermo A. Alvarez, Elizabeth Borowsky, Susie Go, Theodore H. Romer, Ralph Becker-Szendy, Richard Golding, Arif Merchant, Mirjana Spasojevic, Alistair Veitch, and John Wilkes.
Minerva: An automated resource provisioning tool for large-scale storage systems.
ACM Transactions on Computer Systems, 19(4):483-518, 2001.

2

E. Anderson.
Simple table-based modeling of storage devices.
Technical Report HPL-SSP-2001-4, HP Laboratories, July 2001.

3

Eric Anderson, Michael Hobbs, Kimberly Keeton, Susan Spence, Mustafa Uysal, and Alistair Veitch.
Hippodrome: Running circles around storage administration.
In Proc. of Symposium on File and Storage Technologies (FAST), pages 175-188, January 2002.

4

BMC Software.
Patrol for Storage Networking, 2004.

5

E. Borowsky, R. Golding, P. Jacobson, A. Merchant, L. Schreier, M. Spasojevic, and J. Wilkes.
Capacity planning with phased workloads.
In Proceedings of the first international workshop on Software and performance, pages 199-207. ACM Press, 1998.

6

Maria Calzarossa and Giuseppe Serazzi.
Workload characterization: A survey.
Proc. IEEE, 81(8):1136-1150, 1993.

7

D. Chambliss, G. A. Alvarez, P. Pandey, D. Jadav, J. Xu, R. Menon, and T. Lee.
Performance virtualization for large-scale storage systems.
In Proceedings of the 22nd Symposium on Reliable Distributed Systems, pages 109-118, October 2003.

8

Free Software Foundation, Inc., https://www.gnu.org/ software/ glpk/ glpk.html.
GLPK (GNU Linear Programming Kit), 2003.

9

J.S. Glider, C. Fuente, and W.J. Scales.
The software architecture of a san storage control system.
IBM Systems Journal, 42(2):232-249, 2003.

10

Gartner Group.
Total Cost of Storage Ownership--A User-oriented Approach.
Research note, 2000.

11

Hewlett-Packard Laboratories, https:// tesla.hpl.hp.com/ public_software.
Publicly-available software and traces, 2004.

12

Lan Huang, Gang Peng, and Tzi-cker Chiueh.
Multi-dimensional storage virtualization.
SIGMETRICS Perform. Eval. Rev., 32(1):14-24, 2004.

13

IETF Policy Framework Working Group.
IETF Policy Charter. https://www.ietf.org/ html.charters/ policy-charter.html.

14

Raj Jain.
The Art of Computer System Performance Analysis.
Wiley, 1991.

15

Wei Jin, Jeffrey S. Chase, and Jasleen Kaur.
Interposed proportional sharing for a storage service utility.
SIGMETRICS Perform. Eval. Rev., 32(1):37-48, 2004.

16

T. Joachims.
Making large-scale SVM learning practical.
MIT Press, Cambridge, USA, 1998.

17

M. Karlsson, C. Karamanolis, and X. Zhu.
Triage: Performance isolation and differentiation for storage systems.
In Proc. of the 12th. Int'l Workshop on Quality of Service, June 2004.

18

Chenyang Lu, Guillermo A. Alvarez, and John Wilkes.
Aqueduct: online data migration with performance guarantees.
In Proceedings of Conference on File and Storage Technologies (FAST), pages 175-188, January 2002.

19

C. Lumb, A. Merchant, and G. A. Alvarez.
Façade: virtual storage devices with performance guarantees.
In Proc. 2nd Conf. on File and Storage Technologies (FAST), pages 131-144, April 2003.

20

Storage Networking Industry Association, https://www.snia.org.
SMI Specification version 1.0, 2003.

21

Storage Performance Council, https://www.storageperformance.org.
SPC I/O traces, 2003.

22

David Sullivan.
Using probabilistic reasoning to automate software tuning.
PhD thesis, Harvard University, September 2003.

23

Nancy Tran and Daniel A. Reed.
ARIMA time series modeling and forecasting for adaptive i/o prefetching.
In Proceedings of the 15th international conference on Supercomputing, pages 473-485. ACM Press, 2001.

24

J. Turner.
New directions in communications.
IEEE Communications, 24(10):8-15, October 1986.

25

S. Uttamchandani, K. Voruganti, S. Srinivasan, J. Palmer, and D. Pease.
Polus: Growing storage QoS management beyond a 4-year old kid.
In FAST04, March 2004.

26

M. Uysal, G. A. Alvarez, and A. Merchant.
A modular, analytical throughput model for modern disk arrays.
In Proc. of the 9th Intl. Symp. on Modeling, Analysis and Simulation on Computer and Telecommunications Systems, pages 183-192, August 2001.

27

D. Verma.
Simplifying network administration using policy-based management.
IEEE Network Magazine, 16(2), March 2002.

28

D. Verma and S. Calo.
Goal Oriented Policy Determination.
In Proc. 1st Workshop on Algorithms and Architectures for Self-Managing Sys., pages 1-6. ACM, June 2003.

29

Mengzhi Wang, Kinman Au, Anastassia Ailamaki, Anthony Brockwell, Christos Faloutsos, and Gregory R. Ganger.
Storage device performance prediction with CART models.
SIGMETRICS Perform. Eval. Rev., 32(1):412-413, 2004.

About this document ...

CHAMELEON: a self-evolving, fully-adaptive resource arbitrator for storage systems

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons paper.tex

The translation was initiated by Li Yin on 2005-02-17

USENIX '05 Technical Program USENIX '05 Home USENIX home