Machine Learning has been used in many research products that analyze the semantic similarity between binary functions, an analysis often used for security purposes. State-of-the-art methods use either linear stream or control flow graph representations when preprocessing code for ML. We feel these approaches treat binary code too similarly to natural language, overlooking the well-defined semantic structures of binary code. We thus suggest instead using a semantically aware preprocessing. Extensive experiments show that our method significantly outperforms the state-of-the-art.
Binary code similarity detection (BCSD) is a fundamental task that determines the semantic similarity between two binary functions. It serves as a crucial component in addressing various important challenges in the field of software security. For instance, consider a scenario where we have a bunch of vulnerable binary function samples from closed-source libraries or operating systems (e.g., VxWorks) at hand, and we want to see if these vulnerabilities are present in any routers or other relevant devices. We can identify these potential 1-day vulnerabilities by first computing the semantics similarities between these vulnerable functions and all functions in the device firmwares, and then examining the matches with particularly high similarity scores.
However, detecting the semantic similarity between binary functions is challenging. On one hand, two semantically identical functions may exhibit entirely different syntax representations, particularly in cross-architecture scenarios. On the other hand, two semantically different functions can possess similar syntax representations. Thus, it is essential for a BCSD solution to understand the code semantics.
In this article, we will step towards enabling BCSD solutions to understand the semantics of binary code better.
Understanding the semantics of binary code is not a well-defined task that can be solved by traditional hand-written algorithms. Thus, with the development of artificial intelligence techniques, deep learning (DL) based algorithms are naturally introduced [6,10,11]. To ensure scalability, most DL-based BCSD solutions adopt a two-step framework for computing the similarities, as depicted in Figure 1. In the first step, the system learns how to perform a semantic similarity-preserving mapping from binary functions to numerical vectors (which we call embeddings). Subsequently, the similarity between these embeddings is calculated as an approximation to the similarity of functions.

The distinctions among these BCSD solutions primarily lie in their approaches to generating embeddings. Existing embedding methods can generally be classified into two directions, i.e., instruction stream-based and control flow graph (CFG)-based, as illustrated in Figure 2. The former relies on natural language processing (NLP) techniques and generates the embedding directly from the entire instruction stream of the target function. The latter partitions the function into basic blocks, generates embeddings from the instruction streams of these basic blocks, and then fuses the block embeddings into the final code embedding through graph neural networks on the CFG.
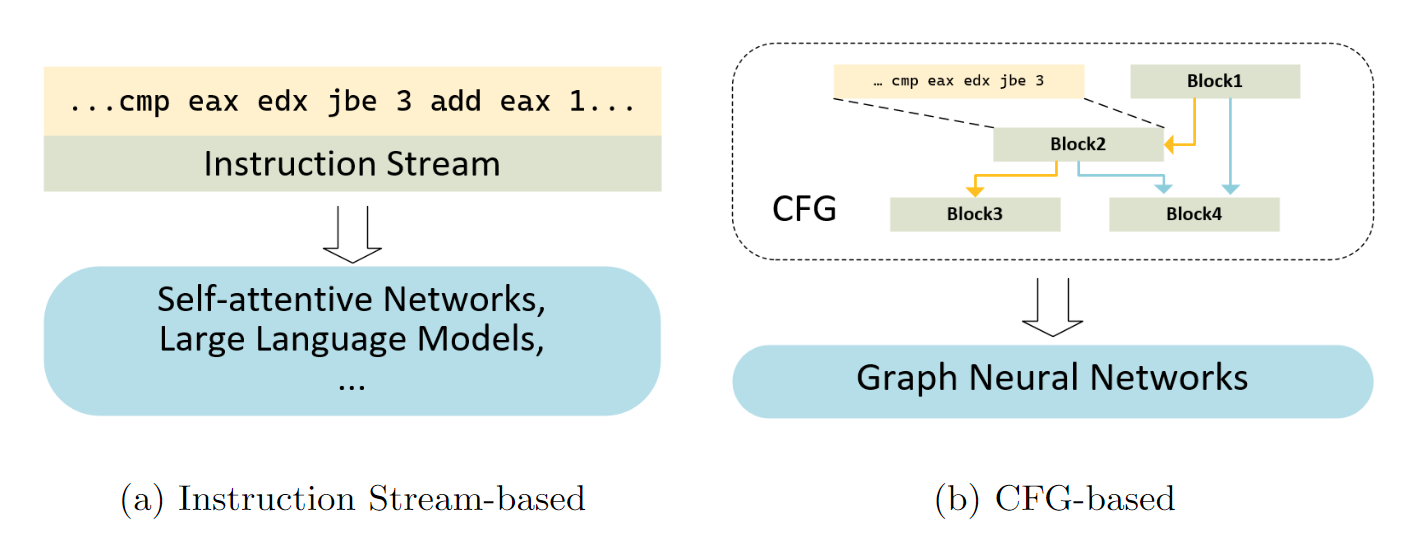
We notice that the stream representation with NLP-based methods that is adopted by the state-of-the-art works in both directions. The underlying assumption behind this prevalence is that natural languages and assembly languages (used by binary code) exhibit fundamental similarities. However, it is noteworthy that despite the resemblance between natural language sentences and instruction streams, they implicitly differ in the following three aspects:
- Natural languages are designed for exchanging information while binary code is designed to match the machine architecture exactly. Natural language sentences are ambiguous and weakly structured while the binary code has well-defined structures, semantics, and conventions. For instance, accurately parsing the syntactic dependency in natural language sentences is challenging, while it is easy in binary code.
- Reordering instructions or moving instructions between basic blocks is feasible, which suggests that binary code should be represented in a more flexible representation rather than sequences of instructions. In fact, instructions are often reordered and moved around basic blocks by the compiler for optimization. However, there is no well-defined way to reorder words or sentences in natural languages while preserving the semantics.
- Binary code can be thought of as consisting only of verbs (instruction codes) and pronouns (register/memory references); natural languages, on the other hand, are rich in syntax. Moreover, when instructions use registers or memory slots, they indeed use the value temporarily cached inside them. The exact registers or memory slots used to cache the value are semantics-independent.
We summarize the differences in the following table:
| Natural Languages | Assembly Languages | |
|---|---|---|
| Purpose | Exchanging information | Machine Execution |
| Structure | Weakly structured | Fully structured |
| Linearity | Naturally linear | More flexible |
| Composition | Abundant | Full of pronouns and verbs |
These differences suggest that treating code as natural languages may be suboptimal, providing an opportunity, one we explored.
Let us take one more step to see how the differences between natural languages and binary code may impede the semantics learning of binary code with NLP-based methods. NLP-based methods consume a sequence of tokens. Abstractly, each token contains two aspects of information, i.e., its token content and its position in the sequence. Take the most famous Transformer-based [9] models as an example. For each input token, its content as well as its position in the sequence are first transformed into two embedding vectors respectively and then summed, as shown in Figure 3a. And the resulting embedding set of tokens is fed to the subsequent networks. Thus, modifying either token content or token position results in different inputs of NLP-based models. If such modification does not change code semantics, these models need to learn from it.

Figure 3 shows three trivial semantically equivalent transformations that the sequence representation imposes on NLP-based models to learn:
For these transformation rules to be learned by models and extended to real-world cases, a lot of related samples need to be learned. For instance, if only code snippets in Figure 3a and Figure 3c are given, models may learn that the given code snippet at position 0 and position k are semantically equivalent, while it is not necessary for them to learn if similar rules hold when another code snippet is given or the snippet is placed at another position. In addition, it costs extra network parameters and layers. Overall, learning these additional semantics makes the NLP-based approaches more expensive and more difficult to generalize.
The semantics-preserving transformations listed above provide several hints on properties that an ideal binary code representation should possess:
- The representation should not assign a position identifier to each instruction or token, as the semantics is independent of position. Therefore, a graph representation would be more appropriate.
- The representation should not fully adopt the execution order to restrict instructions since a significant portion of execution order restrictions is machine-dependent but semantics-independent, which suggests a more flexible control flow representation.
- Some token contents are independent of semantics, while the relations between instructions or tokens carry the semantics. We thus aim to eliminate the semantics-independent tokens and model semantic relations.
To sum up, we want a flexible graph representation for binary code with its edges (representing relations between tokens) emphasized and semantics-independent elements purged. We name such a graph representation a semantics-oriented graph (SOG). We will try to provide an intuitive explanation of what a SOG is by how it is constructed. If you are interested in its technical details, please refer to [2].
Before continuing, we would like to introduce a toy intermediate representation, which is mostly self-explanatory. To avoid unnecessary complexity, we present ideas based on the toy IR. As shown in Figure 4, the toy IR includes four types of tokens, i.e. registers which are of the form ri (e.g. r1), instruction operators which appear as the first token of the instruction or the first token on the right of the equation symbol (e.g. STORE, CALL), integer literals and labels (e.g. L1). Labels mark the start of basic blocks and are used by branch instructions. The exact semantics of toy IR instructions are not our current concern.

We model the construction of SOG in three steps:
First, we lift the sequence of instructions into a graph representation and reveal the relations between instructions as edges. Figure 4b shows an example of such a representation lifted from the code snippet in Figure 4a. This graph can be obtained by enhancing the data flow graph (DFG) with additional control flow (execution flow) and effect flow (necessary execution order) edges. We name this representation the instruction-based semantics-complete Graph (ISCG), as it carries exactly the same semantic information as the original linear representation and takes instructions as nodes. One interesting thing is that we do not mark which basic block an instruction belongs to, because instructions can actually float over basic blocks without changing the semantics, as long as these three types of relations are respected.
Second, we reveal intra-instruction structures by splitting instructions into tokens and translating the structures into edges between tokens. This step simplifies the generation of node embeddings and eases the elimination of semantics-independent elements. The intra-instruction structures can be interpreted as another kind of data relations. For example, we can interpret the instruction r0 = LOAD 0x1000 as the LOAD token using the 0x1000 token and the r0 token using the processed result of the LOAD token. By further refining the inter-instruction relations on the exact instruction tokens which introduce them (i.e., control and effect relations are defined on instruction operators, while data relations are defined on the register tokens or others that temporarily cache data), and labeling the positions of the operands on the edges, we obtain the graph shown in Figure 4c. Edges with omitted labels in this graph have the default label 1 (i.e., these relations are built on their first operands). Figure 4c reveals semantically related inter-instruction relations and intra-instruction structures. We name this representation the token-based semantics-complete graph (TSCG).
Third, since the choice of temporary stores (e.g., registers or stack slots) to cache data between instructions is semantically independent, we further remove these nodes and connect their inputs and outputs directly, forming Figure 4d, the final representation that this study targets.
To demonstrate the efficiency of the SOG representation for BCSD, we select several promising representations from previous work that are not surpassed by others:
In addition, we compare the SOG representation with straw-man representations proposed in the last section:
To compare with those baselines, we keep other parts of our solution, tune only the hyper-parameters tightly related to these methods, and report the best results found. Specifically, we tune only the hyper-parameters of graph encoders and the batch sizes within the constraint of GPU memory (10 GiB). Observing that the result scores of some baselines are close, we repeat experiments 10 times and report mean values to mitigate the effect of randomness.
Following the common practice of previous work [4,10,12], we evaluate our method on the binary function retrieval task, i.e. given a query function f and a pool of N different binary functions, our goal is to retrieve the only ground truth function that is compiled from the same source code as the query function.
Table 1 shows the results of the ablation study. The first section of the table contains the results of baseline representations, in which the CFG-HBMP method stably outperforms the other two methods. The second section shows the results of the straw-man representations. The last section shows the results of the SOG representation.
| XA | XM | x64-XC | |||
|---|---|---|---|---|---|
| 100 | 100 | 10000 | 100 | 10000 | |
| CFG-OPC200 | 92.8/95.6 | 62.9/69.3 | 32.0/38.7 | 64.2/70.3 | 36.8/42.9 |
| CFG-PalmTree | - | - | - | 66.1/72.3 | 36.3/43.0 |
| CFG-HBMP | 94.3/96.6 | 65.3/71.9 | 33.7/40.6 | 67.2/73.0 | 39.0/45.5 |
| P-DFG | 93.4/96.2 | 69.7/76.0 | 37.4/44.7 | 69.9/75.7 | 42.8/49.3 |
| P-CDFG | 94.6/96.9 | 71.1/77.3 | 38.6/45.9 | 72.4/77.8 | 43.6/50.5 |
| P-ISCG | 95.1/97.2 | 71.3/77.2 | 40.1/47.2 | 71.9/77.1 | 44.2/50.9 |
| P-TSCG | 95.5/97.4 | 73.2/78.9 | 41.3/48.8 | 73.5/78.7 | 46.4/52.9 |
| P-SOG | 95.5/97.5 | 74.5/80.2 | 43.8/50.8 | 75.6/80.7 | 48.1/54.6 |
Compared to the baseline representation in the first section of Table 1, the proposed SOG representation improves the recall by nearly 10 percent in all subtasks except XA. XA is the easiest subtask for the GNN and the graph representation-based methods, in which even the CFG-opc200 method can achieve a recall rate as high as 92.8%. And we observe that the relative performance of the SOG over the CFG-HBMP becomes better as the pool size increases from 100 to 10000 in both the XM subtask (from 9.2% to 10.1% in RECALL@1) and the x64-XC subtask (from 8.4% to 9.1% in RECALL@1).
In the second section, the RECALL@1 and MRR scores of P-DFG, P-CDFG, P-ISCG, and P-TSCG generally increase successively, demonstrating that the reveal of control flow relations, effect flow relations, and intra-instruction structures can indeed improve the efficacy. The introduction of effect flow edges slightly hurt the performance in the XC subtask when setting the pool size as 100. This may be attributed to the dirty effect problem which we discuss in Section 6 of our paper [2]. The performance in all subtasks benefits from the introduction of control flow edges and the reveal of the intra-instruction structures.
The P-DFG method outperforms the CFG-HBMP method in nearly all subtasks except XA, which demonstrates the superiority of CFGs in the cross architectures scenario and the superiority of DFGs in the cross-optimization and the cross-compiler subtasks. In addition, the superiority of the SOG over the TSCG supports the hypothesis that keeping the semantics-independent elements in the representation hurts the generalization ability of the model.
Recently, breakthroughs have been made in natural language understanding. Large language models have emerged as frontrunners and have been adapted and specialized for comprehending binary code. Nevertheless, we believe that assembly languages, which are designed for machine execution, are fundamentally different from natural languages. And thus, they deserve special treatment.
In this article, we propose the use of semantics-oriented graph representation, which is a concise and semantics-complete graph representation for binary code. Although we only focus on utilizing this representation for BCSD, it should also be applied to other binary code-related tasks that require understanding the code semantics. Additionally, we have also made efforts to improve the graph neural networks for this representation. However, we are of the opinion that current graph neural networks fall short of fully harnessing the potential of the SOG representation.
For more information on this work, please refer to our publication in USENIX Security 2024 [2].



