


Next: Design and Analysis of
Up: Traffic Modeling
Previous: The Network
Maximum and Minimum Traffic Functions
We define the output traffic function
Ri, X(t) of connection
Mi at the (variable) server X to be the amount of
data of Connection Mi departing from Server X during the time
interval [0,t). Obviously,
Ri, X(t) precisely describes the
traffic of Connection Mi at the output of Server X. The fact that
this function is time-dependent makes it an unlikely candidate for a
traffic descriptor.
We consider two more concise functions, which deterministically bound
the expected traffic of a connection, and therefore can be used as
envelope to characterize the traffic.
We call Function
Fi, X(I) the maximum traffic function
for Connection Mi at Server X if for any I > 0,
That is, the maximum amount of traffic output from Server X for
Connection Mi during any time interval of length I is at most
Fi, X(I).
Similarly, we define
fi, X(I) to be the minimum
traffic function. That is, for any I > 0,
Again, during any interval of length I, the amount of traffic output
from server X for Connection Mi is at least
fi,X(I).
Figure 1:
Maximum Rate Function
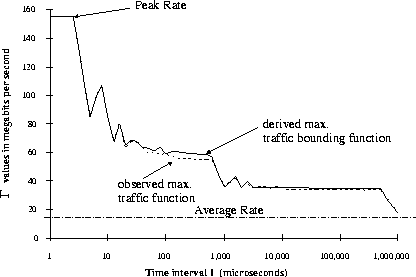 |
Figure 1 shows a related measure, the maximum
rate function
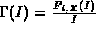 of a traffic flow.
In this example, a traffic stream is measured by a network analyzer as
it enters an ATM network, and the maximum average rate
of a traffic flow.
In this example, a traffic stream is measured by a network analyzer as
it enters an ATM network, and the maximum average rate
 is plotted as a function of the averaging interval I.
is plotted as a function of the averaging interval I.
We use the functions F() and f() as traffic descriptors
for the traffic of connections in the networks. F() and
f() form the tightest deterministic time-invariant
characterization of the traffic at the output of a server. As
F() and f() may be defined by a large number of points,
they are cumbersome to manipulate and bounds on the maximum and
minimum traffic functions are used to characterize the traffic.
We define the maximum traffic bounding function B(I) to be an
upper bound on F(I), that is,
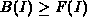 for all I.
Similarly, we define the minimum traffic bounding function
b(I) to be a lower bound on f(I), that is,
for all I.
Similarly, we define the minimum traffic bounding function
b(I) to be a lower bound on f(I), that is,
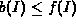 for
all I. Since we base our detection mechanism on B() and
b(), the more tightly they bound the actual traffic, the more
accurate is the resulting classification into compliant and
non-compliant traffic.
for
all I. Since we base our detection mechanism on B() and
b(), the more tightly they bound the actual traffic, the more
accurate is the resulting classification into compliant and
non-compliant traffic.
In the context of real-time communication protocols, maximum traffic
bounding functions are used to allocate resources, and tight bounding
functions are sought to prevent excessive over-allocation of network
resources. In practice, a trade-off must be made between tightness of
the bounding function on one side, and the overhead incurred to
manipulate it on the other, together with the inherent a-priori
uncertainty about the traffic characteristics at the sources.
Traffic functions can be easily approximated with piecewise linear
bounding functions at any level of resolution. Consider a maximum
traffic function F(). Assume that we know one point of the
function F(), that is, we know
B' = F(I') for some value of
I'. We then have a first-order approximation of F(I), which is
given by
This can be recursively used to bound the function if more points are
known. In this form, coarse bounds (three to five linear segments) on
maximum traffic functions can be used for resource allocation
purposes, where a broad categorization of traffic streams into classes
- for example teleconference, or advertising, or sports - is
sufficient. More accurate bounds (say, ten linear segments) can then
be used to closely characterize individual traffic streams.
Once the traffic bounding functions are known at the entrance to the
network, they can be derived for any point along the path of a
connection. This derivation requires to obtain the traffic at the
output of a server from the traffic at its input.
Let X and Y be two adjunct servers, and let Connection Mi first
traverse Server X and then Server Y. Then,
Fi,Y(t) = Fi, X(t + d)
and
fi,Y(t) = fi, X(t - d)
where d is the worst-case delay experienced by Connection Mi at
Server Y. The value for d depends on the scheduling methodology
used in the server and on the traffic functions of other connections
using that server. For a FCFS service discipline, for example, the
worst-case delay on Server X can be bounded as follows, assuming
that Server X serves N connections, and the traffic of a
connection Mj is bounded at the output of the previous server by
the maximum traffic bounding function
Bj,PREV():
Various analytical techniques to derive worst-case delays based on
traffic bounding functions for other scheduling policies, such as
Static Priority, Generalized Processor Sharing, and various forms of
Earliest-Due-Date have been proposed
([4, 5, 7, 8, 12]
among many others). The
above formula imply that, for Server Y, the upper and lower traffic
at its output, modeled by
Bi,Y(t) and
bi,Y(t), can be
derived from the traffic at its input (i.e., the output of the
previous Server X).
Figure 2:
Maximum and Minimum Traffic Function Define an Envelope
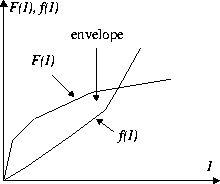 |
Figure 2 illustrates how the maximum and minimum
traffic functions define an envelope for the amount of traffic on the
connection at the output of a server. The network will, during run
time, dynamically examine the traffic and verify if the traffic
lies within this envelope. In the case of a violation is found,
then a (potential) intrusion is detected. Actions can be taken to
immediately suppresses the violation. These functionalities are
implemented in a security device, which we discuss next.


Next: Design and Analysis of
Up: Traffic Modeling
Previous: The Network
Riccardo Bettati
1999-02-23


![]() for all I.
Similarly, we define the minimum traffic bounding function
b(I) to be a lower bound on f(I), that is,
for all I.
Similarly, we define the minimum traffic bounding function
b(I) to be a lower bound on f(I), that is,
![]() for
all I. Since we base our detection mechanism on B() and
b(), the more tightly they bound the actual traffic, the more
accurate is the resulting classification into compliant and
non-compliant traffic.
for
all I. Since we base our detection mechanism on B() and
b(), the more tightly they bound the actual traffic, the more
accurate is the resulting classification into compliant and
non-compliant traffic.