New Abstractions for Data Parallel Programming

James C. Brodman, Basilio B. Fraguela $^\dag$ , María J. Garzarán, and David Padua

$\textstyle \parbox{5in}{{{ Department of Computer Science \\ University of Illi... ...s.edu \\ \\ $^\dag$Universidade da Coru\~{n}a,Spain \\ basilio@udc.es \\ } }}$

Abstract:

Developing applications is becoming increasingly difficult due to recent growth in machine complexity along many dimensions, especially that of parallelism. We are studying data types that can be used to represent data parallel operations. Developing parallel programs with these data types have numerous advantages and such a strategy should facilitate parallel programming and enable portability across machine classes and machine generations without significant performance degradation.

In this paper, we discuss our vision of data parallel programming with powerful abstractions. We first discuss earlier work on data parallel programming and list some of its limitations. Then, we introduce several dimensions along which is possible to develop more powerful data parallel programming abstractions. Finally, we present two simple examples of data parallel programs that make use of operators developed as part of our studies.

1 Introduction

The extensive research in parallel computing of the last several decades produced important results, but there is still much room, and much need, for advances in parallel programming including language development. New programming notations and tools are sorely needed to facilitate the control of parallelism, locality, processor load, and communication costs.

In this paper, we present preliminary ideas on data types (data structures and operators) that can be used to facilitate the representation of data parallel computations. A data parallel operation acts on the elements of a collection of objects. With these operations, it is possible to represent parallel computations as conventional programs with the parallelism encapsulated within the operations. This is of course an old idea, but we believe it is also an idea with much room for advances. We have chosen to study data parallel notations because most parallel programs of importance can be represented as a sequence of data parallel operations. Furthermore, scalable programs, which are the ones that will drive the evolution of machines, must be data parallel. The strategy of representing parallel computations as a sequence of data parallel operations has several advantages:

Conventional notation. Data parallel programs written as sequences of data parallel operations can be understood as conventional programs by ignoring parallelism. Although understanding how the parallelism is exploited is necessary to analyze performance, in this paradigm it is not necessary to understand the semantics of the program. We believe that using a conventional notation reduces the likelihood of errors, facilitates maintenance, and shortens the learning process. These benefits of a conventional notation were the main motivation behind the work on autoparallelization [23].
Higher level of abstraction. A judicious selection of operators should lead to very readable programs where powerful operators encapsulate parallelism.
Control of determinacy. Whenever the data parallel operators are implemented as pure functions, the programs will be guaranteed to be determinate, although this comes at the cost of having an implicit barrier after each data parallel operator. Avoiding these barriers may require compiler transformations. If non-determinacy is desired, it can be encapsulated inside the parallel operators by allowing interaction with a global state.
Portability. Data parallel programs written as a sequence of operations can be ported across classes of parallel machines just by implementing the operators in different ways. Thus, the same program could be executed on shared-memory and distributed-memory multiprocessors as well as on SIMD machines. In the same way that parallelism is encapsulated by the operations, so can be the nature of the target machine. Programmers would of course need to consider portability when developing a program and must choose algorithms that perform well across machine classes.
Good performance abstractions. By understanding the performance of each operation it is possible to determine the overall performance of the program.

The rest of this paper is organized as follows. In Section 2, we discuss the data parallel operators of the past. Possible directions of evolution for data parallel operators are discussed in Section 3 and two examples of data parallel codes built with some of the data types we have developed are presented in Section 4. Conclusions are presented in Section 5.

2 Data Parallel Programming

There is an extensive collection of data parallel operators developed during the last several decades. This collection arises from several sources. First, many of today's data parallel operators were initially conceived as operators on collections. Parallelism seems to have been an afterthought. Examples include the map [21] and reduce [26] functions of LISP, the operation on sets of SETL [25], and the array, set, and tree operators of APL [17]. The reason why these operators can be used to represent parallel computation is that many parallel computation patterns can be represented as element-by-element operations on arrays or other collections or as reduction operations. Furthermore, parallel communication patterns found in message passing (e.g. MPI) parallel programs correspond to operations found in APL, and more recently Fortran 90, such as transposition or circular shifts. Most of these operations were part of the languages just mentioned.

The vector instructions of SIMD machines such as the early array and vector processors, including Illiac IV [3], TI ASC [27], and CDC Star [14] are a second source of data parallel operators. Array instructions are still found today in modern machines including vector supercomputers and as extensions to the instruction set of conventional microprocessors (SSE [16] and Altivec [9]) and as GPU hardware accelerators [20], with their hundreds of processors specialized in performing repetitive operations on large arrays of data.

The the data parallel operators of high-level languages and the libraries developed to encapsulate parallel computations are a third source of data parallel operators. Early examples of data parallel languages include the vector languages of Illiac IV such as Illiac IV Fortran and IVTRAN [22]. Recent examples include High Performance Fortran [19,12] that represented distributed memory data parallel operations with array operations [1] and data distribution directives. The functional data parallel language NESL [5] made use of dynamic partitioning of collections and nested parallelism. Data parallel extensions of Lisp (*Lisp) were developed by Thinking Machines. Data parallel operations on sets was presented as an extension to SETL [15] and discussed in the context of the Connection Machine [13], but it seems there is not much more about the use of data parallel operation on sets in the literature. The recent design of a MapReduce [8] data parallel operation combining the map and reduce operators of Lisp has received much attention.

In the numerically oriented high-level languages, data parallel programming often took the form of arithmetic operations on linear arrays perhaps controlled by a mask. Most often, the operations performed where either element-by-element operations or reductions across arrays. An example from Illiac IV Fortran is A(*) = B(*) + C(*) which adds, making use of the parallelism of the machine, vectors B and C and assigns the result to vector A. In Fortran 90 and MATLAB the same expression is represented by replacing * with :. In IVTRAN, the range of subscripts was controlled with the do for all statement (the predecessor of today's forall). Reductions were represented with intrinsic functions such as sum, prod, any, and first.

Two important characteristics of the operations on collection and data parallel constructs of the languages described above are:

Flat data types. In practically all cases, there is no internal hierarchy of the data structures. Arrays, sets, sequences are typically flat data structures. An exception is NESL which makes use of sequences of sequences for nested parallelism. HPF accepted declarations specifying data partitioning and alignment, but these were instructions to the compiler and not reflected directly in the executable instructions.
Fully independent parallelism. In all cases, parallelism is either fully independent or, if there is interaction, takes the form of a reduction or scan operations.

Despite the great advantages mentioned in Section 1, there is much less experience with the expression of parallelism using operators on collections than with other forms of parallelism. Parallel programming in recent times has mostly targeted MIMD machines and relied on SPMD notation, task spawning operations and parallel loops. Even for the popular GPUs, the notation of choice today, CUDA, is SPMD. The most significant experience with data parallel operators has been in the context of vector machines and vector extensions (SSE/Altivec) where data parallel operators are limited by the target machine, like in the Illiac IV days, to element-by-element simple arithmetic or boolean vector operations.

3 Extending the Data Parallel Model

Advances in the design of data parallel operators should build on earlier work, some of which was described in Section 2. However, to move forward it is also necessary to consider parallel programming patterns that demonstrate their value for programmability or performance. An example is tiling which occurs frequently in all forms of parallel programs for data distribution in distributed memory machines, to control loop scheduling in shared-memory machines, or to organize the computation in GPU programs. Another example is the dynamic partitioning of data for linear algebra computations or sorting operations. A third example is data parallel operations in which operations on different elements of a collection interact with each other or must be executed in a particular order. Interactions and ordering between operations on elements of a collection have traditionally been associated with task parallelism, but they can also be implemented within data parallel operations.

In our experience, specific evolution directions for the functionality of data parallel operators include:

New classes of collections. Although there have been proposals and a few experimental systems that apply data parallelism to general collections of objects, most of the implementations and hence of the experience has targeted dense arrays. However, sparse computations and operations on sets (and perhaps other objects such as graphs) must be considered if data parallel operators are to become universally useful.
Static and dynamic partitioning or tiling. To enable the direct control of data distribution and scheduling, it must be possible to partition, dynamically and statically, the collections that the data parallel operators manipulate. It must also be possible to directly operate on these partitions. In the case of arrays, the simplest and most useful partitions are tiles. In fact, the numerous algorithms developed using static and dynamic tiling seems to indicate that tiling is a fundamental operation on collections [10]. Tiling can be applied at one or multiple levels. When tiling at multiple levels, the outermost levels of tiling can be used to distribute the work between the threads in a parallel program, while the innermost levels are used to enhance locality. When the target is a distributed-memory system, tiles can make communication explicit, because computations involving elements from different tiles result in data movement.
We have studied partitioned collections including tiled dense and sparse arrays and partitioned sets. To operate on arrays, we developed the Hierarchically Tiled Array (HTA) data type. We programmed several codes including the NAS benchmarks and some well known numerical algorithms such as LU and found that the programs written using HTAs resulted in shorter and more readable codes than their MPI counterparts, while obtaining similar performance results [4,11]. We have obtained similar results when comparing HTAs to SMP APIs such as TBB [2,7]. We are currently investigating how to add partitions or tiles to data parallel operation on sets, to obtain a tiled (or hierarchically tiled) set. A tiled set is similar to an HTA, with the only difference that in this case the programmer needs to define a, potentially complex, mapping function to determine the tile to which an element of the set belongs. In the case of arrays, tiling can be defined by hyperplanes along each dimension.
Tile size can be used to control how the load is distributed among processors. While partitioning a dense array in equal chunks is easy, the partition of a sparse array or a set into equal-size chunks is not trivial. In the case of tiled sparse array, the programmer may choose different tiling strategies depending on the structure of the sparse arrays. In the case of the tiled sets, different mapping functions can result in different distributions. When a good tile size cannot be determined a priori, a possible solution to ameliorate the problem of load imbalance is to create more tiles than threads and let the runtime system map the tiles to the threads, following a task stealing strategy similar to the one implemented in Cilk [6] or Intel Thread Building Blocks [24] or Charm++ [18].
Parallel operations with interactions. Another example of patterns that have not been traditionally programmed using data parallel operators are operations on collections with interactions between the computations on different elements, thus requiring the usage of locks or other forms of synchronization for correctness. As an example, consider A(I) += V where A, I and V are vectors. 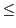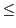This expression means that for every i, 1 $\leq$ i $\leq$ n, where n is the length of I and V, A(I(i)) must be updated adding to it the value of V(i). As mentioned in the previous section, traditional data parallel operators require the computation to be fully parallel, so vector I cannot have two elements with the same value. However, in many situations, collections of two or more elements of I may have the same value, so that some elements of A could be augmented repetitively with elements from V. Thus, to obtain a correct result, the elements of A must be atomically updated. Otherwise, a mechanism to impose an order of execution would be needed.
In principle, assuming that the potential rounding errors of floating-point operations can be disregarded, updates to an element of A could be reordered. In this case, we will have a non-determinate computation with the results varying, perhaps only slightly, depending on the order of updates. There are of course numerous other cases where non-determinacy could arise. The difference between results could be significant without affecting correctness. However, in these cases, non-determinacy could be encapsulated within the data parallel operation, facilitating analysis.
In other cases, the order of operation is relevant. For example, assume A represents the balances of bank accounts, and V a sequence of amounts to be drawn from (negative) or credited to (positive) the accounts indicated by the corresponding index in I, with the transactions in V sorted chronologically. If the bank imposes a penalty for negative balances, the transactions associated to each individual account cannot be reordered. Imposing an order of execution of the element operations within a collective operation is an important strategy that can enable the implementation of classes of parallel computations typically associated with task parallel implementations. An example are pipelined computations which can be represented with a doacross schedule within a data parallel operation.
Implementation. The implementation of data types for data parallelism is also an important consideration. While it may seem natural to design the data types and their operators as part of a programming language, in our work we have chosen to use class libraries initially. Creating a new language requires a compiler for each target machine on which the programs are run. Libraries only require a regular host compiler and therefore libraries are easier to develop, enabling fast testing of the usability and performance limitations of new operators. However, compilers are likely to be needed for a production system. Building semantic information into a compiler would allow optimizations that are difficult or impossible with a library, such as eliminating unnecessary copying or temporaries. Furthermore, the high level notation typical of data parallel operators presents the opportunity for advanced optimizations such as data structure selection, static autotuning, and data-dependent dynamic optimizations. Object-oriented languages are the natural implementation language for a library, since what we are designing are new data types. Useful language features are polymorphism and operator overloading, as they allow the representation of operations in a more convenient notation.
Portability. Judiciously designed data parallel data types can be implemented for all classes of parallel machines: distributed-memory clusters, shared-memory multiprocessors, SIMD machines, and machines with hybrid architectures such as distributed memory machines with SMP nodes and array extensions. The performance optimality of an implementation will likely differ across machine classes, but the code will at least be portable across machine classes. The desired degree of portability should be taken into account when selecting the algorithms during program development.
Performance abstractions. Determining efficiency of execution or approximate running times by inspecting a program is useful for manual tuning and obtaining guarantees on the execution time of the codes. Estimating execution time is a difficult task even for conventional programs. However, the encapsulation of computations inside operations on collections could contribute to facilitate performance prediction. It would certainly be useful to associate with data parallel operators an execution model for each class of target machines. Although performance abstractions would be complicated by the application of the advanced optimizations just mentioned, it should be possible to either give lower bounds on performance or give formulas that specify behavior as a function of parameters representing different execution conditions including characteristics of the data and data placement at the beginning of the execution of an operator.

4 Examples of Data Parallel Programs

In this Section we show two code examples with data parallel operators on tiled data structures. Section 4.1 describes merge sort using tiled arrays. Section 4.2 describes a graph breadth-first search algorithm that uses tiled sets.

4.1 Merge Sort

Merge sort is used to illustrate the use of tiled arrays and nested parallelism. For tiled arrays we used the HTA data type described in [4,11]. HTAs are arrays whose components are tiles which can be either lower level HTAs or conventional arrays. Nested parallelism could proceed recursively across the different levels of the tile hierarchy. This hierarchy can be specified statically or dynamically when the tiling structure depends on the input characteristics.

Figure 1 illustrates the use of a dynamic partitioning operator (addPartition) to produce nested parallelism on merge sort. As the Figure shows, HTA input1 is first split in half. Then, the location of the element greater than the midpoint element of input1 is found in input2 and used to partition it. Then output is partitioned such that its tiles can accommodate the respective tiles from the two input tiles that are going to be merged. Finally, an hmap recursively calls the Merge operation on the newly created left tiles of the two input arrays as well as the right tiles.

hmap takes as arguments a function, a tiled structure (array or set), and optionally, additional structures with the same arrangement of tiles. The function is applied to corresponding tiles and this application can take place in parallel across corresponding tiles. hmap can perform basic element-by-element operations, but it can also be used to perform more complex user-defined actions upon elements or tiles. More examples of HTAs can be found in [4,11].

**Figure 1:** Parallel Merge
$\begin{figure}{ \begin{center} \scriptsize \begin{verbatim} Merge(HTA out... ...ge(), output, input1, input2)\end{verbatim} \par \end{center} } \end{figure}$

4.2 Bread-First Search

Bread-First Search (BFS) illustrates the use of sets to implement a graph search algorithm that traverses the neighboring nodes starting at the root node. For each node, it traverses their unvisited neighbor nodes. It continues this process until it finds the goal node. Our example, shown in Figure 2, uses a BFS strategy to label the nodes in the graph by level, where level is the shortest path length from the initial node.

Our data parallel implementation uses tiled sets, meaning that sets of nodes are partitioned into tiles and a mapping function is used to determine to which tile a node belongs. A tiled set is similar to an HTA in functionality, the only difference being that the underlying primitive data type is a set instead of an array.

**Figure 2:** Breadth-First Search
$\begin{figure}{ \begin{center} \scriptsize \begin{verbatim} TiledSet work... ... + 1) work_list_tile.add(e)\end{verbatim} \end{center} } \par \end{figure}$

This algorithm uses the following data structures:

work_list - a set of nodes partitioned into tiles. Tiles can be processed in parallel with each other. Mapping_function(e) computes the tile, i, of work_list to which node e belongs.
neighbors - a tiled set that represents the neighbors of the the nodes in work_list in each iteration of the while loop. Tile i of neighbors contains the neighbors of tile i of work_list. However, nodes in tile i of neighbors do not necessarily belong to tile i of work_list.
rearranged_neighbors - a tiled set that consists of the elements of neighbors rearranged using mapping_function used to control tiling within the work_list set.
adj - a tiled set that holds the adjacency information of the graph on which the search is performed. Each element is a pair consisting of a node and a set of neighbors that can be reached from that node. Given a node e, adj(e) is the set of its neighbors. Pairs are mapped by applying to the first element of adj the same mapping function used for the work_list set.

5 Conclusions

Although numerous parallel programming paradigms have been developed during the past several decades, there is consensus that a notation with the most desirable characteristics is yet to be developed. Problems of modularity, structure and portability remain to be solved.

Data types for data parallel programming have the potential of addressing these problems. Well designed data types should enable the development of highly structured, modular programs that resemble their sequential counterparts in quality of their structure and at the same time enable portability across classes of parallel machines while maintaining efficiency. Although experience with data parallel programming models has been limited in scope and quantity, our own experience with this approach has convinced us that it is promising. We are yet to see a computational problem that does not succumb to the data parallel programming paradigm. Much remains to be done for programmability and performance. New data types and powerful methods for old data types need to be designed and tools for optimization must be developed, but there is no question that significant advances are coming and that data parallel programming will have a significant role in the future of computing.

Acknowledgements

This material is based upon work supported by the National Science Foundation under Awards CCF 0702260, CNS 0509432, and by the Universal Parallel Computing Research Center at the University of Illinois at Urbana-Champaign, sponsored by INTEL Corporation and Microsoft Corporation. Basilio B. Fraguela was partially supported by the Xunta de Galicia under project INCITE08PXIB105161PR and the Ministry of Education and Science of Spain, FEDER funds of the European Union (Project TIN2007-67537-C03-02).

Bibliography

1: J. C. Adams, W. S. Brainerd, J. T. Martin, B. rian T. Smith, and J. L. Wagener.
Fortran 90 Handbook.
McGraw-Hill, 1992.
2: D. Andrade, J. Brodman, B. Fraguela, and D. Padua.
Hierarchically Tiled Arrays Vs. Intel Threading Building Blocks for Programming Multicore Systems.
In Programmability Issues for Multi-Core Computers, 2008.
3: G. H. Barnes, R. M. Brown, M. Kato, D. Kuck, D. Slotnick, and R. Stokes.
The ILLIAC IV Computer.
IEEE Transactions on Computers, 8(17):746-757, 1968.
4: G. Bikshandi, J. Guo, D. Hoeflinger, G. Almasi, B. B. Fraguela, M. J. Garzarán, D. Padua, and C. von Praun.
Programming for Parallelism and Locality with Hierarchically Tiled Arrays.
In Proc. of the ACM SIGPLAN Symp. on Principles and Practice of Parallel Programming, pages 48-57, 2006.
5: G. E. Blelloch.
NESL: A Nested Data-Parallel Language.
Technical report, Pittsburgh, PA, USA, 1992.
6: R. D. Blumofe, C. F. Joerg, B. C. Kuszmaul, C. E. Leiserson, K. H. Randall, and Y. Zhou.
Cilk: An efficient multithreaded runtime system.
In Proc. of the ACM SIGPLAN Symp. on Principles and Practice of Parallel Programming, pages 207-216, 1995.
7: J. Brodman, B. Fraguela, M. J. Garzaran, and D. Padua.
Design Issues in Parallel Array Languages for Shared Memory.
In 8th Int. Workshop on Systems, Architectures, Modeling, and Simulation, 2008.
8: J. Dean and S. Ghemawat.
MapReduce: Simplified Data Processing on Large Clusters.
Commun. ACM, 51(1):107-113, 2008.
9: S. Fuller.
Motorola's Altivec Technology.
Technical report, Motorola, Inc, 1998.
10: J. A. Gunnels, F. G. Gustavson, G. M. Henry, and R. A. van de Geijn.
FLAME: Formal Linear Algebra Methods Environment.
ACM Trans. Math. Softw., 27(4):422-455, 2001.
11: J. Guo, G. Bikshandi, B. B. Fraguela, M. J. Garzarán, and D. Padua.
Programming with Tiles.
In Proc. of the ACM SIGPLAN Symp. on Principles and Practice of Parallel Programming, pages 111-122, Feb 2008.
12: High Performance Fortran Forum.
High Performance Fortran specification version 2.0, January 1997.
13: W. D. Hillis.
The Connection Machine.
MIT Press series in artificial intelligence, 1985.
14: R. G. Hintz and D. P. Tate.
Control Data STAR-100 Processor Design.
In Proc. of COMPCON, pages 1-4, 1972.
15: R. Hummel, R. Kelly, and S. Flynn Hummel.
A Set-based Language for Prototyping Parallel Algorithms.
In Proceedings of the Computer Architecture for Machine Perception '91, 1991.
16: Intel Corporation.
IA32 Intel Architecture Software Developer's Manual (Volume 1: Basic Architecture), 2004.
17: K. E. Iverson.
A Programming Language.
John Wiley & Sons, Inc., New York, NY, USA, 1962.
18: L. Kale and S. Krishnan.
CHARM++: A Portable Concurrent Object Oriented System Based on C++.
In Proceedings of the Conference on Object Oriented Programming Systems, Languages and Applications, pages 91-108, 1993.
19: C. Koelbel and P. Mehrotra.
An Overview of High Performance Fortran.
SIGPLAN Fortran Forum, 11(4):9-16, 1992.
20: D. Luebke, M. Harris, J. Krüger, T. Purcell, N. Govindaraju, I. Buck, C. Woolley, and A. Lefohn.
GPGPU: General Purpose Computation on Graphics Hardware.
In ACM SIGGRAPH 2004 Course Notes, page 33, 2004.
21: J. McCarthy.
LISP 1.5 Programmer's Manual.
The MIT Press, 1962.
22: R. Millstein and C. Muntz.
The Illiac IV Fortran Compiler.
10(3):1-8, March 1975.
23: D. A. Padua and M. J. Wolfe.
Advanced Compiler Optimizations for Supercomputers.
Commun. ACM, 29(12):1184-1201, 1986.
24: J. Reinders.
Intel Threading Building Blocks: Outfitting C++ for Multi-core Processor Parallelism.
O'Reilly, 1 edition, July 2007.
25: J. Schwartz.
Set Theory as a Language for Program Specification and Programming, 1970.
26: G. Steele.
Common Lisp: The Language.
Digital Press, Newton, MA, USA, 1990.
27: W. Watson.
The TI-ASC, A Highly Modular and Flexible Super Computer Architecture.
In Proc. AFIP, pages 221-228, 1972.

About this document ...

New Abstractions for Data Parallel Programming

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation paper.tex

The translation was initiated by James Brodman on 2009-03-04

James Brodman 2009-03-04