Practical Data-Centric Storage

Cheng Tien Ee - UC Berkeley
Sylvia Ratnasamy - Intel Research, Berkeley
Scott Shenker - ICSI & UC Berkeley

Abstract:

1. Introduction

Deployments of wireless sensor networks (WSNs) in recent years have grown steadily in their functionality and scale [25,31,1,13,3,18,34], but they still operate under extreme energy constraints. Hence, the ability to efficiently extract relevant data from within the WSN remains paramount. In their seminal paper [6], Estrin et al. argue that efficient data-retrieval in WSNs requires a paradigmatic shift from the Internet's node-centric style, in which the basic communication abstraction is point-to-point (or multipoint) delivery, to a data-centric approach in which query and communication primitives refer to the names of sensed data rather than the identity (e.g., network address) of the sensing node.

The first generation of data-centric methods addressed the conveyance of data through the network. Directed diffusion [14], the first such proposal, determined data routes (and rates) based on reinforcement feedback from upstream nodes, resulting in tree-like data paths from the various sensing nodes to the base station (by which we mean the source of queries). A later method, TinyDB/TAG [23,24], explicitly constructs a delivery tree and then performs various forms of data manipulation as the data is conveyed to the base station.

A later generation of data-centric methods, inspired by the use of Distributed Hash Tables (DHTs) in the Internet, has focused on the storage rather than the conveyance of data. These solutions use intelligent in-network storage to make data retrieval more efficient. In data-centric storage, sensed data are stored, by name, within the network. All data with the same name are stored at a single node, so queries can be routed directly (rather than flooded) to the node that stores the desired data. Data-centric storage (DCS) can be used to support a variety of sophisticated query primitives such as multidimensional range queries [22,11], multi-resolution queries [10], and approximate queries [12]. However, there has yet been any deployment in sensornets, though there are multiple scenarios in which they will be useful. For instance, we can imagine a sensor network deployed in a safari, monitoring the location of the various animals. Rather than querying each node to determine if it has seen an elephant, we can instead query a single node that is responsible for all elephant sightings.

These two classes of methods, data-centric conveyance and data-centric storage, have very different performance characteristics in terms of the energy expended to get the desired data. As discussed in [30] for the simplest cases of data-centric conveyance and storage, their relative performance depends on the nature of the data generation, the query rate, the network size, and many other factors.

More to the point of this paper, these two classes of methods require very different communication primitives from the network. The various data-centric conveyance methods rely (either implicitly or explicitly) on tree-construction techniques. Note that even the simplest method of data conveyance, whereby all data are proactively sent to the base station immediately upon generation, also relies on a spanning delivery tree. Tree-based routing is both algorithmically simple and practically robust, leading to its adoption in a number of real-world deployments. For example, simple proactive data delivery was used in the deployments on Great Duck Island [25,31] and Intel's fabrication unit [3], while TinyDB is used in the deployments at the UCB botanical gardens [18].

In contrast, all known data-centric storage methods rely on a point-to-point routing primitive: they deterministically map the name (say x) of a data item to the routable address (say i) associated with a particular node. Node i is then responsible for storing all data named x and all queries for x are routed directly to node i, thereby requiring point-to-point routing.

However, as we review in the following section, achieving scalable and practical point-to-point routing is a difficult challenge. While a number of recent research efforts [27,28,17,20,11,8] have made significant progress towards this end, point-to-point routing still requires significantly more overhead and complexity than tree construction as we will explain in the following section, and has yet to be used in real-life deployments. It thus seems unwise to couple data-centric storage to such a burdensome underlying primitive, particularly one that is not widely deployed. If data-centric storage is to become more widely used, it should rely only on currently available, and easily implementable, communication primitives.

Our goal is not merely to find a better algorithm for data-centric storage. More fundamentally, we hope to make data-centric storage a basic primitive available to WSN applications, and we recognize that this can only happen if data-centric storage is implemented with minimal assumptions about the underlying infrastructure.

To that end, this paper proposes a data-centric storage method called pathDCS that uses only tree-based communication primitives. The design relies on associating data names with paths, not nodes, and these paths are derived from a collection of trees. We investigate some basic performance issues, such as load balance, through high level simulation but for a more real-world evaluation we implemented pathDCS in TinyOS and report on its performance in packet-level TOSSIM[21] simulations as well as in experiments on a mote testbed. To the best of our knowledge, this is the first evaluation of a working prototype of data-centric storage. Our results show that pathDCS achieves high query success rates (on our 100-node testbed, we see roughly a 97% success rate) and is robust to node and network dynamics.

Finally, we note that in this paper we only consider the basic exact-match storage primitives as explored by schemes such as GHT [29] and GEM [27]. We leave for future work its possible extension to supporting the more complex query primitives from the literature [22,12,10,9].

2. Background

The value of pathDCS relies on four basic points:

1. Data-centric storage is a valuable paradigm in WSNs.

2. Current data-centric storage techniques rely on point-to-point routing.

3. Point-to-point routing is difficult, and imposes significant overhead on WSNs.

4. pathDCS provides a scalable and robust implementation of data-centric storage that does not require point-to-point routing.

The bulk of this paper is devoted to demonstrating the fourth point. In this section, we briefly review the literature supporting the first three.

Point # 1

Reference [30] presented only the simplest form of data-centric storage: an exact-match query-by-name service where the named data can be directly retrieved. A number of subsequent proposals extend the idea of data-centric storage to support more complex queries such as multi-dimensional range queries [22,11], multi-resolution indexing [10] and spatially distributed quadtree-like indices [12].

Point # 2

While elegant in structure, this approach requires that nodes know the network's external geographic boundary so that names are mapped to geographic locations within the network. If they don't, most data will end up stored by edge nodes, after an extensive perimeter walk, resulting in uneven load and inefficient operation. The various proposals acknowledge, but do not address, this challenge.

Point # 3

In recent work, Kim et al. [17] and Leong et al. [20] proposed extensions to GPSR that removes the need for the unit-disc assumption. CLDP [17] represents a fundamental breakthrough in that it guarantees correct operation over topologies with even arbitrary connectivity. GDSTR [20] on the other hand routes on spanning trees when greedy forwarding is unable to make progress. In both cases additional complexity and overhead is required.

An even more basic assumption underlying geographic routing is that each node knows its geographic coordinates. While some sensor nodes are equipped with GPS, the widely-used Berkeley mote is not: although other localization techniques do exist, none of them have been evaluated for their potential to serve as routing coordinates. Motivated by this challenge, GEM [27] and NoGeo [28] explore the construction of virtual coordinate systems; these are synthetic coordinates to which geographic routing can be applied. Like CLDP, GEM and NoGeo represent significant conceptual advances but come at the cost of increased complexity. NoGeo requires O(N) per-node state during initialization while GEM can incur significant overhead under node and network dynamics.

Finally, there are a number of proposals for point-to-point routing in the literature on ad-hoc wireless networks. Many of these solutions face scalability problems when applied to wireless sensor networks and are thus unlikely to serve as a substrate for DCS. We refer the reader to [8] for a more detailed discussion of the space of point-to-point routing algorithms and their applicability to WSNs.

As the above discussion reveals, there has been significant progress on point-to-point routing for WSNs and both BVR and CLDP have resulted in working implementations for the mote platform. At the same time, the various solutions remain fairly complex (at least relative to tree construction) and face further challenges in supporting in-network storage. For these reasons, we deemed it worthwhile to explore an alternate approach that releases DCS from the challenges and complexities of point-to-point routing.

3. Design

We begin this section with the description of the core pathDCS algorithm, followed by those of supporting ones.

3.1 Core Algorithm

For pathDCS to be effective, it must be consistent: that is, all queries and stores for the same object (no matter from where they are issued) must reach the same destination. The traditional way to ensure consistency is to give all nodes a shared frame of reference that allows packets to describe their destination and enables forwarding nodes to route packets to that destination. We use a few shared points of reference called landmarks (places with well-known names that all nodes can reach), and name locations by their path from one of these shared points of reference [32]. For example, when giving driving directions (in real life) we often use a well-known landmark and then provide path-based instructions: ``Go to the gas station, and then take your first right, and then after two blocks take a left...." The driver need only know (a) how to find the landmarks and (b) how to follow a set of procedural directions. This is the approach used in pathDCS. We map each name to a path, not a node, and that path is defined by an initial landmark and a set of procedural directions that are defined in terms of other landmarks. To query or store that name, a packet goes to the designated landmark and then follows a set of procedural directions; the store or query is then executed at the node on which the path ends. Notice that the end-point of the path is independent of where the query or store is issued from; since the path starts off by going to a particular landmark, its origin doesn't matter.

In pathDCS the landmarks are a set of beacon nodes, which can be elected randomly or manually configured (see Section 3.2). To make sure that all nodes know how to reach the beacons, we use standard tree-construction techniques to build trees rooted at each one of these beacons. The overhead to establish the necessary state is proportional to the number of beacons; as we will see, that number is small so pathDCS imposes little overhead.

The paths are specified in terms of an initial beacon and a set of segments, with each segment consisting of a direction (defined in terms of a beacon) and a length (defined by how many hops). Thus, each path consists of a sequence of p beacons b_i and lengths l_i, where i = 1,..., p.¹ The packet is first sent to beacon b₁. From there, it is sent l₂ hops towards beacon b₂ using the tree rooted at b₂. The process then repeats; from wherever the packet ended up at the previous i - 1 segment, it is then sent l_i hops towards the next beacon b_i. The path ends after the pth segment.

To make this more precise, we first define some terms. There is a linear space of identifiers, say 16-bit addresses, that is large enough so that there are no clashes in identifier assignments. Each node in the network is assigned a logical identifier id. Data is associated with a key k (assume this is derived from a hash of its name) and, for node n, the hop distance to beacon b is given by hops(n, b). Let n_i denote the identifier of the node on which the ith segments starts (also the place where the previous segment ends). Lastly, there is some hash function h(k, i) which maps an identifier k and an integer i into an identifier.

When accessing a data item with identifier k, the set of beacons used for the path are determined by consistent hashing [15]: beacon b_i is the beacon whose identifier is closest to (in the sense of consistent hashing) the identifier h(k, i). In addition, the first segment length l₁ is always equal to the distance to the first beacon b₁, whereas segment lengths for i > 1 are given by:

Figure 1: (a), (b) and (c) show the routing trees rooted at beacons b₁, b₂ and b₃ respectively. (d) Source nodes s₁ and s₂ both send packets with the same key. These packets first reach a common first beacon (b₁), before taking the same subsequent path segments to reach destination node d.

We use Figure 1 as an example to illustrate how pathDCS routes packets with the same key from different source nodes to the same destination node. For clarity we show the routing trees rooted at b₁, b₂ and b₃ in Figures 1a, 1b and 1c respectively. We fix the total number of path segments at 3, and both source nodes s₁ and s₂ generate packets with the same key k. Both the current number of remaining hops and the current path segment i (also called segment counter) are carried in the packet header and modified as needed. In the figure, beacons b₁, b₂ and b₃ are chosen because their ids are closest to h(k, 1), h(k, 2) and h(k, 3) respectively. The order of beacons towards which packets are forwarded is therefore b₁, b₂ and b₃, following the order of segments traversed. Initially, both packets are routed to b₁, upon which it is determined, using Equation 1, that in the second segment they should be forwarded towards b₂ for, say, 1 hop. At node t, which is the terminating node of the second segment, the segment counter in the packet header is incremented, the number of hops is again computed using Equation 1 (assume the result is two), and the packets are subsequently forwarded two hops towards the third and final beacon, to terminate at node d. Node d is then the destination node for all data associated with key k.

The number of hops required for each query or store is proportional to the diameter of the network, which is the same for all DCS approaches, multiplied by the number of segments. Thus, the key to keeping the overhead of pathDCS manageable is keeping the number of segments, p, small. As we argue below, p = 2 is sufficient for reasonably-sized networks, so that we expect the per-query expenditure to be a few multiples bigger than in other DCS schemes.

The pathDCS algorithm has two parameters: B, the total number of beacons and p, the number of path segments. Varying B trades off the control traffic overhead due to tree construction versus load on the beacons. We explore this tradeoff in Section 5. With regards to p, increasing the number of segments results in longer paths but potentially spreads the storage load more evenly. To see this how large p should be to achieve reasonable load distribution, consider the following naive back-of-the-envelope calculation. The total number of paths a message can traverse using pathDCS is approximately B^p. Letting d be the network density and r the radio range, the expected length of each path is given by

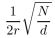(2)

(3)

(4)

3.2 Supporting Algorithms

While the basic idea of pathDCS is contained in the core algorithm defined above, actual implementation of pathDCS requires a set of supporting algorithms to, for example, select beacons and build trees. There is nothing novel in these algorithms, we describe them for completeness.

Tree Construction

Beacon Election

It is possible that the election process results in two or more beacons clustering. An additional rule can be imposed to reduce the occurrence of this scenario: when timeout occurs and just before a node announces itself as a beacon, it checks to see if any beacons lie within k hops. If so, it suppresses its announcement.

Beacon Handoff and Failure

Responding to Queries

Data Refreshing

Data Replication

4. Performance Metrics

The design of pathDCS raises three performance questions. The first has to do with the consistency with which pathDCS maps names to storage locations. In the absence of node and network dynamics, pathDCS achieves perfect consistency in that stores and lookups for a particular data item always terminate at the same storage node, and hence pathDCS would see a 100% success rate for lookups. However, node and network dynamics can lead to changes in the paths to beacons and hence to changes in the mapping between a name and storage node. The extent to which such changes impact lookups depends on both the frequency and the extent of changes. If changes in storage nodes are highly localized, then simple local replication of data should trivially mask such changes. If changes are infrequent, then a periodic refresh of stored data should suffice to maintain high success rates. In any case, pathDCS provides only weak consistency: it does not guarantee that the data retrieved is the latest stored.

These path changes are primarily dependent on the behavior of the wireless medium and hence we explore this issue in detail in Section 6. However, such changes are also dependent on network size because longer paths are more likely to experience changes. Since we can't analyze scaling effects on our testbed, we use an idealized, but highly pessimistic, model of path dynamics in our simulator to see how consistency varies with system size. To quantify consistency, we measure the lookup success rate, which is the probability that a lookup for a data item x reaches a storage node currently storing x. To understand the magnitude of lookup variations, we also measure the maximum separation in hops between any two nodes storing a particular data item, which we call the spread. This measures the extent to which local replication can mask the effect of path dynamics.

The second performance issue has to do with how effectively pathDCS balances the storage and forwarding load across nodes. This is a potential issue because unlike other DCS schemes that explicitly distribute data items over the set of all nodes, pathDCS distributes data over a more limited number of paths. While we do not expect pathDCS to achieve load distribution comparable to the address-based DCS schemes, we would like to verify that the load distribution in pathDCS is not unreasonable.

5. High-Level Simulation Results

5.1 Overview

The performance of pathDCS derives from the inherent behavior of its algorithms as well as the impact of the wireless medium on both the algorithms and our particular implementation choices. To separate the effects of each, we evaluate pathDCS through a combination of high-level simulations (to evaluate the scaling behavior of the algorithms themselves), low-level simulations that take into account a lossy medium and packet collision effects, and implementation (to evaluate pathDCS under realistic wireless conditions). This section presents our high-level simulation results; our prototype and its evaluation in TOSSIM [21] and on actual testbeds are described in Section 6.

Our simulator makes a number of simplifying assumptions that abstract away the vagaries of the wireless medium. Nodes are placed uniformly at random in a square plane and every node is assigned a fixed circular radio range. A node can communicate with all and only those nodes that fall within its radio range. In addition, the simulator does not model network congestion or packet loss. While clearly unrealistic, these simplifications allow simulations that scale to thousands of nodes; our packet-level simulation and testbed results in the following section capture performance under more realistic conditions.

Our default simulation scenario uses 5000 nodes placed in an area of 6.7 x 10⁴ units² with a radio range of 8 units, leading to an average node degree of 14.5. We maintain the same density for all simulations.

Figure 2: Success rate under failure and randomized parent selection for increasing network sizes. All tests use 20 beacons and 2 path segments.

Figure 3: Spread under failure and randomized parent selection for increasing network sizes. All tests use 20 beacons and 2 path segments.

Figure 4: CDF of storage load with pathDCS and ``optimal'' DCS for different numbers of beacons.

Figure 5: CDF of transmission load with pathDCS and ``optimal'' DCS for different numbers of beacons.

Figure 6: CDF of storage load using pathDCS for increasing network sizes.

Figure 7: CDF of transmission load using pathDCS for increasing network sizes.

5.2 Lookup Success Rates

We perform the following test to measure success rates: for a network with N nodes, every node inserts 10 distinct data items into the network yielding a total of 10 x N distinct data items. Stores are replicated within the one-hop neighborhood of the destination. We then perform 20 lookups for each data item. A lookup succeeds if it arrives at a node storing the requested data item (either at the original destination, or at one of the one-hop replicas); otherwise, the lookup fails. To measure spread, we repeat the same tests as above but now we turn off one-hop replication and have each node store (rather than lookup) every data item 20 times. For each data item, we then consider the set of nodes storing that item and measure spread as the maximum separation in hops between any two nodes in the set.

To capture the effect of node failure, after each of the 20 iterations for a given item, we fail a fixed fraction of nodes uniformly at random and then recompute the trees for each beacon. Capturing varying link qualities is more problematic because our simulator does not model congestion and packet loss; instead, we directly address the effect on parent selection. We conservatively model changes in parent selection arising from varying link qualities as follows: rather than pick a single parent for each beacon, a node considers all of its neighbors that are closer to the destination beacon than itself as potential parents. For every message, a node then chooses its next hop uniformly at random from this entire set of potential parents. This represents a highly pessimistic scenario in which, at every hop, the route to a beacon can flap between all possible next-hops.³

Recall that fixed parent selection with no failure has a success rate of 100% and a spread of zero since we turn off one-hop replication when measuring spread. Figures 2 and 3 plot the average success rate and spread under increasing network size using random parent selection or fixed parent selection under various failure rates. As expected, we see that the success rate drops, and spread rises with network size but this deterioration is slow. For example, a 10,000 node network with random parent selection (which, again, is a pessimistic model) still sees a success rate of 92%. Moreover, the absolute value of spread is often low and hence could frequently be masked by simple k-hop local replication. We implement just 1-hop replication but for very large networks (>10,000 nodes) with high failure rates (30%) one might need a larger scope of replication.

Section 6 continues this evaluation in real wireless environments.

5.3 Load Distribution

There are only two knobs to the basic pathDCS algorithm: (1) the total number of beacons and (2) the number of path segments used. Ideally, we want to pick a number of beacons and path segments that allow forwarding and storage load to be well spread out while maintaining reasonable path stretch. The analysis in Section 3 leads us to the choice of 2 segments and hence we now look at the number of beacons required to achieve good load distribution.

We first hold N, the network size, fixed at 5000 nodes and scale B, the number of beacon nodes. As before, every node uses pathDCS to insert 10 distinct data items into the network yielding a total of 50,000 distinct stored items. We then measure the per-node forwarding and storage load. Figures 4 and 5 plot the cumulative distribution function (CDF) of the storage and transmission load respectively. To determine if any load imbalances are due to pathDCS, or are inherent in the DCS approach, we also plot the distributions for an ``optimal'' form of DCS in which names are mapped uniformly at random over the entire set of nodes and stores follow the shortest path from the inserting node to the destination storage node.⁴ In terms of storage, we see that usage of just 20 beacons results in a fairly even distribution and that increasing B beyond 20 offers rapidly diminishing returns. In terms of transmission load, we see that the pathDCS distribution approaches that of the optimal although both are fairly skewed. This is due to the natural concentration of traffic in the center of the grid and is in no way specific to pathDCS or even DCS schemes in general; rather this is an issue for communication in all ad hoc networks and one that has received some attention in the literature [26].

At less than 1% of the total number of nodes, B = 20 represents very low control overhead in terms of tree construction. Moreover, we see that the pathDCS distributions are reasonably close to the optimal node-based DCS. Given the relative simplicity of pathDCS, this seems like a very worthwhile tradeoff.

We now investigate the variation of performance with increasing network size. We fix B = 20 and scale N. Figures 6 and 7 plot the CDF of transmission and storage load respectively. We see that, as expected, the distribution deteriorates with increasing N but this deterioration is very gradual.

Finally, the stretch in all our tests was approximately 2.4 which is in keeping with our use of 2 path segments. We also verified that stretch increases as we increase the number of path segments.

In summary, this section explored the basic scaling behavior of the pathDCS algorithms. We show that pathDCS is robust in that it achieves high success rates under highly pessimistic models of node and network dynamism. Moreover, pathDCS is scalable in that it requires a small number of beacons to achieve good load distribution.

6. Implementation Details and Results

We implemented pathDCS in TinyOS, and evaluated its performance on the 100-node Intel Mirage [4] micaZ testbed as well as on 500 nodes in TOSSIM's packet-level emulator. We begin this section by briefly describing the pathDCS system architecture, followed by low-level details of the implementation in TinyOS, and finally ending with evaluation of its performance.

6.1 PathDCS System Architecture

Figure 8: The pathDCS architecture is made up of (1) the data plane, consisting of the forwarding engine and data storage and replication component, and (2) the control plane, consisting of the tree construction and related components.

Figure 8 shows the pathDCS system architecture, which can be divided into control and data planes. The control plane provides primarily beacon election and tree-based routing capability, whereas the data plane implements the core pathDCS forwarding logic (using the control plane's tree-based routing tables), storage of name-value pairs, and one-hop replication. Note that the only component specific to pathDCS is the forwarding engine; the remaining components are common to a number of other systems such as TinyDB [24] and BVR [8].

6.2 Control Plane

Node Identifier

Beacon Election

Link Quality Estimation

Tree Construction

Control packets and fields

6.3 Data Plane

In this paper, the data plane operations of interest include the forwarding of pathDCS data packets and their replication. The description of these operations is followed by an brief coverage of the packet header overhead.

Forwarding

Replication

Data packets and fields

6.4 Methodology

Thus, as in Section 5, we are primarily interested in the probability of lookup success. A lookup can fail either because the message was dropped along the way, or because the destination node it arrived at did not have the requested data. Two metrics are used to distinguish between these two causes. The first is the route completion probability, measured as the probability that a packet successfully arrives at a destination node (as opposed to being dropped along the path). Note that the route completion probability has little to do with the pathDCS algorithms per se. Instead, such failures are dependent primarily on the characteristics of the wireless medium and our implementation choices for the link estimation, tree construction and retransmission modules. In general the quality of links in the network fluctuates over time, resulting in route updates as the network attempts to pick routes that result in lower loss.

The second performance metric is our usual lookup success rate as defined in Section 4. In computing this rate, we consider only those lookups that complete (that is, they reached some destination node), and we say that a lookup is successful if it locates the requested data item. To measure the effect of variable node and network conditions, we obtained the lookup success rate for different values of data refresh intervals. This is achieved as follows: in each experiment, we have all nodes periodically route some number of messages for each distinct data item. For the routes that do complete, we then observe where those messages terminate. Next, we divide time into windows, where the first data packet in that window is treated as a store or refresh packet, and the node at which it terminates is the storage node for that window. Subsequent packets then act as queries and lookup success is measured as the probability that a lookup arrives within the one-hop neighborhood⁷ of the storage node for that window. We do this for each distinct data item, compute the average lookup success and repeat for different window sizes. We note that varying this window size is equivalent to altering the data refresh interval, and we can thus use a single experiment to observe the effect of increasing refresh intervals rather than running repeated experiments that may suffer from different time-of-day effects.

Data refreshing plays a crucial role in improving lookup success, especially in large networks (of size in the hundreds to thousands), where the path may vary widely over time. When we consider short time-scales, say within a period of a minute or two, the set of destination nodes for a particular key is probably small in number, and not likely to be spread out over a large region. However, when looking at all possible destinations over a period of a day, the set of nodes will be the union of all sets at shorter time-scales: it is more likely to be large, as well as covering a wider area. Thus, a refresh rate that is high translates into observation at small time-scales, which means that destinations are close together, and therefore lookup success increases. We validate this in the following sections, via simulation and experiments on the testbed.

6.5 TOSSIM Simulations

In this section we describe packet-level simulations that model a lossy medium. A total of 500 nodes were simulated using actual TinyOS code. We begin by elaborating on the parameters used in the simulations as well as in the testbed's motes.

Control plane parameters

Data plane parameters

In each experiment, every node in the network generates different data items, thus data destined for a particular destination node originate from multiple sources. On average, data packets are injected into the network at the rate of two per second to minimize congestion. A total of 20 experiments are run, with each experiment querying or storing a particular, distinct key, and each node sending 72 packets. The network is allowed to run for a simulation hour for routing to converge before queries and storage began.

With the above parameters, we measure the route completion probability, the destination node spread distribution, and the lookup success rate under two test scenarios:

Normal

Fast Route Adaptation

Figure 9: The measure of destination spread distribution is based on the hop distance from the node that received the most packets (i.e. the mode).

Figure 10: 500-node simulation: distribution of destinations for the normal and fast route adaptation scenarios.

Since paths are likely to change over time, we need to investigate the destination spread distribution. Even though we expect the spread of destination nodes to be significant, the situation is not hopeless if we find that most of the packets still fall within a small region. Using Figure 9 as an illustration, we proceed as follows: we first determine the node that received the most number of packets for a particular key, we call this the mode node. Then, for each hop from the mode node, we compute the total fraction of packets that end on nodes at that distance. If the destination nodes are evenly spread out over a wide area, then the distribution will show a relatively flat graph over multiple hops. On the other hand, if the nodes are highly clustered together, we should see a graph that peaks at the 0th hop, with small fractions at the other hops.

Observations

1. The majority of packets (80%) land within one hop of the mode node. This implies that, without data refreshing and with one hop replication, the mean probability of lookup success will also be about 80%. As we shall see subsequently, data refreshing increases this probability. Another alternative will be to increase the scope of local replication, which will however be at the expense of more transmissions and storage space.
2. Having more dynamic routing does not affect the resulting destination spread. This is due to the fact that, over time, all possible combinations of routing state, and correspondingly all possible destinations, have been encountered. Increasing the rate at which changes occur does not affect this destination set.

Figure 11: 500-node simulation: variation of lookup success with data refresh interval.

We next consider the effect of data refreshing. As described in Section 6.4, lookup success now refers to average fraction of queries that end within the replication region for all window periods. These periods, or refresh intervals, are varied from 5 to 250 seconds, and the results are shown in Figure 11. We can observe that

1. Refreshing data more frequently can increase the probability of a successful query to >95%.
2. Faster route adaptation results in lower lookup success for a particular refresh interval.
3. Variation in lookup success is higher for routing that updates more frequently.
4. As the refresh interval increases, lookup success probability approaches that of packet fraction received within one hop of the mode node, which agrees with Figure 10.

Overhead Scaling

Figure 12: 500-node simulation: breakdown of transmissions for each packet type.

Finally, we consider the overhead incurred by pathDCS, focusing on the total number of each type of packet transmitted. We identify five types of packets: (1) distance vector (DV), (2) link estimation, (3) data packet transmission for replication, (4) data packet transmission for forwarding, and (5) data packet transmission for refreshing. Figure 12 shows the breakdown for various application data generation rates. We assume that the refresh per data type occurs once every 100 seconds, and that there are 100 data types in the network. The rest of the network parameters are as given in Tables 1 and 2. From the figure, we see that the fraction of overhead packets reduces with an increase in application rate, which is what we expect in general. Furthermore, the cost of refreshing data is low, compared to the initial data replication and forwarding.

To summarize, the 500-node packet-level simulation shows that local replication by itself is sufficient to result in high (80%) lookup success. Refreshing data periodically counters the effects of routing changes, and is able to increase lookup success to (>95%). However, the tradeoff is that more packets are transmitted, increasing the overhead incurred.

We now proceed to evaluate the performance of pathDCS on the Intel Mirage testbed.

6.6 Testbed Details and Results

Figure 13: Location of sensor motes of the Intel Mirage testbed is indicated by the stars.

The Mirage testbed is located indoors, covering an entire floor of the building. The 100 micaZ motes are spread out over an area of approximately 160' by 40', at the locations indicated in Figure 13. Each mote in the testbed has a serial interface that is connected to an internal ethernetwork, which in turn is accessible via the Mirage server. Binaries are uploaded and data downloaded via this ethernetwork, with the server providing timestamping service for downloaded data packets. We reduce the transmission power of the motes to reduce the effective density of the network. For all our experimental results in this section, the diameter of the network is 6. Packet generation, test scenarios and network parameters are the same as that of the packet-level simulations in Section 6.5.

Results

Figure 14: Distribution, or spread, of the destination node. The fraction of packets landing x-hops away from the node with the highest fraction is shown.

Figure 15: Probability of lookup success for particular data refresh intervals.

On the other hand, when we consider data refresh, a routing system that is more dampened increases the chances of lookup success. Figure 15 shows the corresponding lookup success probabilities for these two systems. Four observations can be made from the figure:

1. The lookup success is very high in both cases even with low refresh rates, which agrees with the observation in Figure 14 that the set of possible destination nodes is small.
2. With increased damping, the system, in particular the paths, are more stable, resulting in less variation in lookup success.
3. For a given refresh rate, lookup is generally worse for a more adaptive control plane.
4. pathDCS constructed over a more dynamic routing control plane has to refresh its stored data more frequently in order to meet more stringent lookup success requirements.

In conclusion, the performance of pathDCS ultimately relies on the choice of parameters at the underlying control plane. Although the instability of paths causes the set of destination nodes to increase, we find that in general they tend to be highly clustered, with the majority of packets terminating on a small subset. Thus path fluctuations can be countered via two mechanisms: an increase in the scope of local replication, or an increase in the frequency of data refreshes. The former trades off storage space and additional transmissions for an increase in lookup success, whereas the latter trades off additional transmissions. From our results we believe that pathDCS is a feasible and simple way to implement data-centric storage in WSNs.

7. Summary

This paper describes a new approach to implementing data-centric storage (DCS). Our goal was not merely to find a new DCS algorithm, but to develop a more practical approach to DCS, one that does not rely on point-to-point routing. While point-to-point routing may one day be ubiquitously available in WSNs, it is not widely available now and current implementations are either based on idealized radio behavior or incur significant overhead and complexity. In contrast, tree construction primitives are widely available, and are becoming a rather standard component in most WSN deployments. Thus, DCS has a far better chance to become a basic and widely deployed WSN primitive if it only depends on tree-based routing.

From simulations and actual deployment, we see that the primary obstacle, namely fluctuating paths, can be overcome via the usage of local replication and data refreshing. Although these two mechanisms are not perfect in that they incur additional overhead, nonetheless they perform well enough for pathDCS to be of use in large WSNs.

Bibliography

1

ALLEN, M., AND ET AL.
Habitat sensing at the James San Jacinto Mountains Reserve.
Tech. rep., CENS, March 2003.

2

BOSE, P., MORIN, P., STOJMENOVIC, I., AND URRUTIA, J.
Routing with guaranteed delivery in ad hoc wireless networks.

3

BUONADONNA, P., GAY, D., HELLERSTEIN, J. M., HONG, W., AND MADDEN, S.
TASK: Sensor network in a box.
In European Workshop on Sensor Networks EWSN (2005).

4

CHUN, B., AND BUONADONNA, P.
Intel mirage testbed.
Tech. rep., Intel, 2005.

5

COUTO, D. D., AGUAYO, D., BICKET, J., AND MORRIS, R.
A high-throughput path metric for multi-hop wireless networks.
In Proceedings of the 9th Annual MOBICOM (2003), ACM Press.

6

ESTRIN, D., GOVINDAN, R., HEIDEMANN, J., AND KUMAR, S.
Next century challenges: Scalable coordination in sensor networks.
In Proceedings of the 5th Annual MOBICOM (1999), ACM Press.

7

FLOYD, S., JACOBSON, V., MCCANNE, S., LIU, C., AND .ZHANG, L.
A reliable multicast framework for light-weight sessions and application level framing.
In Proceedings of SIGCOMM (1995), ACM Press, pp. 342-356.

8

FONSECA, R., RATNASAMY, S., ZHAO, J., EE, C.-T., CULLER, D., SHENKER, S., AND STOICA, I.
Beacon-vector: Scalable point-to-point routing in wireless sensor networks.
In Proceedings of the Second USENIX/ACM NSDI (Boston, MA, May 2005).

9

GANESAN, D., ESTRIN, D., AND HEIDEMANN, J.
DIMENSIONS: Why do we need a new data handling architecture for sensor networks?
In Proceedings of the ACM HotNets (Princeton, NJ, USA, October 2002), ACM, pp. 143-148.

10

GANESAN, D., GREENSTEIN, B., PERELYUBSKIY, D., ESTRIN, D., AND HEIEMANN, J.
An evaluation of multi-resolution storage for sensor networks.
In Proceedings of the First SenSys (2003), ACM Press, pp. 63-75.

11

GAO, J., GUIBAS, L. J., HERSHBERGER, J., AND ZHANG, L.
Fractionally cascaded information in a sensor network.
In IPSN'04: Proceedings of the third international symposium on Information processing in sensor networks (New York, NY, USA, 2004), ACM Press, pp. 311-319.

12

GREENSTEIN, B., ESTRIN, D., GOVINDAN, R., RATNASAMY, S., AND SHENKER, S.
DIFS: A Distributed Index for Features in Sensor Networks.
In Proceedings of First IEEE WSNA (May 2003).

13

HAMILTON, M., ALLEN, M., ESTRIN, D., ROTTENBERRY, J., RUNDEL, P., SRIVASTAVA, M., AND SOATTO, S.
Extensible sensing system: An advanced network design for microclimate sensing, June 2003.

14

INTANAGONWIWAT, C., GOVINDAN, R., AND ESTRIN, D.
Directed Diffusion: a scalable and robust communication paradigm for sensor networks.
In Proceedings of the 6th Annual MOBICOM (2000), ACM Press, pp. 56-67.

15

KARGER, D. R., LEHMAN, E., LEIGHTON, T., LEVINE, M., LEWIN, D., AND PANIGRAHY, R.
Consistent hashing and random trees: Distributed caching protocols for relieving hot spots on the world wide web.
In Proc. 29th ACM STOC (May 1997), pp. 654–-663.

16

KARP, B., AND KUNG, H. T.
GPSR: Greedy perimeter stateless routing for wireless networks.
In Proceedings of the 6th annual MOBICOM (2000), ACM Press, pp. 243-254.

17

KIM, Y. J., GOVINDAN, R., KARP, B., AND SHENKER, S.
Geographic routing made practical.
In Proceedings of the Second USENIX/ACM NSDI (Boston, MA, May 2005).

18

KLING, R., ADLER, R., HUANG, J., HUMMEL, V., AND NACHMAN, L.
The intel mote platorm: A bluetooth based sensor network for industrial monitoring applications.

19

KUHN, F., WATTENHOFER, R., ZHANG, Y., AND ZOLLINGER, A.
Geometric ad-hoc routing: Of theory and practice.
In 22nd ACM PODC (2003).

20

LEONG, B., LISKOV, B., AND MORRIS, R.
Geographic routing without planarization.
In Proceedings of the Third USENIX/ACM NSDI (San Jose, CA, May 2006).

21

LEVIS, P., LEE, N., WELSH, M., AND CULLER, D.
TOSSIM: accurate and scalable simulation of entire tinyos applications.
In SenSys '03: Proceedings of the 1st international conference on Embedded networked sensor systems (New York, NY, USA, 2003), ACM Press, pp. 126-137.

22

LI, X., KIM, Y. J., GOVINDAN, R., AND HONG, W.
Multi-dimensional range queries in sensor networks.
In Proceedings of the First SenSys (2003), ACM Press, pp. 63-75.

23

MADDEN, S.
The Design and Evaluation of a Query Processing Architecture for Sensor Networks.
PhD thesis, UC Berkeley, 2003.

24

MADDEN, S., FRANKLIN, M., HELLERSTEIN, J., AND HONG, W.
TAG: a tiny aggregation service for ad hoc sensor networks.
In OSDI (2002).

25

MAINWARING, A., POLASTRE, J., SZEWCZYK, R., CULLER, D., AND ANDERSON, J.
Wireless sensor networks for habitat monitoring.
In Proceedings of ACM WSNA (Atlanta, GA, Sept. 2002).

26

NATH, B., AND NICULESCU, D.
Routing on a curve.
SIGCOMM Comput. Commun. Rev. 33, 1 (2003), 137-142.

27

NEWSOME, J., AND SONG, D.
GEM: Graph embedding for routing and data-centric storage in sensor networks without geographic information.
In Proceedings of the First SenSys (2003), ACM Press, pp. 76-88.

28

RAO, A., RATNASAMY, S., PAPADIMITRIOU, C., SHENKER, S., AND STOICA, I.
Geographic routing without location information.
In Proceedings of the 9th Annual MOBICOM (2003), ACM Press, pp. 96-108.

29

RATNASAMY, S., KARP, B., SHENKER, S., ESTRIN, D., GOVINDAN, R., YIN, L., AND YU, F.
Data-centric storage in sensornets with GHT, a geographic hash table.
Mob. Netw. Appl. 8, 4 (2003), 427-442.

30

SHENKER, S., RATNASAMY, S., KARP, B., GOVINDAN, R., AND ESTRIN, D.
Data-centric storage in sensornets.
SIGCOMM Comput. Commun. Rev. 33, 1 (2003), 137-142.

31

SZEWCZYK, R., POLASTRE, J., MAINWARING, A., ANDERSON, J., AND CULLER, D.
An analysis of a large scale habitat monitoring application.
In Proceedings of the Second SenSys (2004), ACM Press.

32

TSUCHIYA, P. F.
The Landmark Hierarchy: a new hierarchy for routing in very large networks.
In ACM SIGCOMM (1988), ACM Press, pp. 35-42.

33

WOO, A., TONG, T., AND CULLER, D.
Taming the underlying challenges of reliable multihop routing in sensor networks.
In Proceedings of the First SenSys (2003), ACM Press, pp. 14-27.

34

XU, N., RANGWALA, K., CHINTALAPUDI, D., GANESAN, D., BROAD, A., GOVINDAN, R., AND ESTRIN, D.
A wireless sensor network for structural monitoring.
In Proceedings of the Second SenSys (2004), ACM Press.

35

ZHAO, J., AND GOVINDAN, R.
Understanding packet delivery performance in dense wireless sensor networks.
In Proceedings of the First SenSys (2003), ACM Press, pp. 1-13.

Footnotes

...p.¹

Note that the labeling of the beacons b_i is idiosyncratic to a path; that is, the indices i merely refer to the ordering of beacons in this particular path. We don't introduce a notation for an absolute labeling of the beacons.

... area,²

resulting in an average of 14 neighbors

... next-hops.³

Note that we restrict parent changes to those that are localized in that they do not trigger a re-computation of the tree downstream from the changing node. The effects of non-localized changes are captured by the tests for node failure.

... node.⁴

In practice, implementing this form of optimal DCS would require every node to have global knowledge of all the nodes in the system as well as shortest path point-to-point routing.

... address⁵

The TOS_LOCAL_ADDRESS in TinyOS.

... keys.⁶

To accomodate more keys we can simply use more bits.

... neighborhood⁷

This reflects the local one-hop replication.

... 86%,⁸

Since the network diameter is large, we expect the end-to-end loss probability to become significant, even with the use of link-level retransmissions. Thus, this does not reflect on pathDCS, only the underlying packet loss behavior.