Fixing Races for Fun and Profit: How to use access(2)

Drew Dean¹
Computer Science Laboratory, SRI International
ddean@csl.sri.com

Alan J. Hu²
Dept. of Computer Science, University of British Columbia
ajh@cs.ubc.ca

Abstract:

It is well known that it is insecure to use the access(2) system call in a setuid program to test for the ability of the program's executor to access a file before opening said file. Although the access(2) call appears to have been designed exactly for this use, such use is vulnerable to a race condition. This race condition is a classic example of a time-of-check-to-time-of-use (TOCTTOU) problem. We prove the ``folk theorem'' that no portable, deterministic solution exists without changes to the system call interface, we present a probabilistic solution, and we examine the effect of increasing CPU speeds on the exploitability of the attack.

1 Introduction

Since the 1988 Morris worm, and particularly the 1996 tutorial on stack smashing in Phrack [1], the buffer overflow has been the attacker's weapon of choice for subverting system security. Many techniques for preventing or mitigating the effects of the lack of memory safety have appeared in the literature [9,14,12,13,3]. Prior to the popularization of stack smashing, various race conditions were commonly utilized as the key step in privilege escalation attacks, i.e., gaining superuser privileges on a machine to which one has access via an ordinary account. While not quite as catastrophic as a buffer overflow in a network server that hands out superuser privileges to anyone who knows the magic packet to send, local privilege escalation attacks remain a serious threat. This is particularly true as another security vulnerability may give the attacker the ability to execute code of their choice as an unprivileged user. Given the wide range of privilege escalation attacks on many common operating systems, it is very difficult to prevent an attacker from ``owning'' a machine once they can get the first machine instruction of their choice executed. Hence, one is wise to expend great effort to make sure that the attacker cannot execute the first instruction of an attack. If we could prevent privilege escalation, we would have more confidence in the ability of lower-level operating system primitives to contain the damage of security vulnerabilities exposed to the network. We make one of many required steps towards that goal in this paper.

One particular race condition is especially infamous among developers of security-critical software, particularly setuid programs, on Unix and Unix-like systems: the one between an appearance of the access(2) system call, and a subsequent open(2) call. Although this paradigm appears to have been the intended use of access(2), which first appeared in V7 Unix in 1979, it has always been subject to this race condition. Recall that individual Unix system calls are atomic, but sequences of system calls offer no guarantees as to atomicity. This is a long standing problem: a 1993 CERT advisory [7] documents this exact race condition in xterm, and earlier exploits based on this problem are believed to exist. However, there is no generally available, highly portable, correct solution for providing the functionality of access(2). This paper remedies this unfortunate situation. It is commonly accepted that fixing this problem requires a kernel change. While this is true for a deterministic solution, we present a highly portable probabilistic solution that works under the existing system call interface. The technique used is reminiscent of hardness amplification as found in the cryptology literature [16], but applied to system calls, rather than cryptologic primitives.

We first survey the problem, its history, partial solutions, and related work. We then prove the ``folk theorem'' that there is no (deterministic) solution to the problem short of a kernel modification. We present our probabilistic solution, and experimental data showing the exploitability of the problem across several generations of machines. Final thoughts are presented in the conclusion.

2 Background

We first describe the problem that we are solving, explain why some known partial solutions are not optimal, and describe related work on this problem.

2.1 The Problem

One of Unix's patented innovations was the introduction of the setuid bit on program files, to indicate that a program should execute with the privileges of its owner, rather than the user that invoked the program, as is the normal case. As more sophisticated programs were developed using the setuid facility, there was desire to have the ability to do access control checks based on the invoker of the program (i.e., the real user id of the program, as opposed to the effective user id of the program). The kernel is clearly the proper place to perform these checks, as pathname parsing and traversal is tricky, particularly since the introduction of symbolic links in 4.2 BSD [2]. This need was addressed with the addition of the access(2) system call to V7 Unix in 1979. It appears that the intention was for the following code fragment:

if(access(pathname, R_OK) == 0)
  if((fd = open(pathname, O_RDONLY))
       == 0) ...

to work in the obvious way - that is, to check whether pathname is readable, and if so, open the file for reading on file descriptor fd.

Unfortunately, there is a classic time-of-check-to-time-of-use (TOCTTOU) [11] problem lurking here: the pair of access(2) and open(2) system calls is not a single, atomic operation. Hence, a clever attacker can change the file system in between the two system calls, to trick a setuid program into opening a file that it should not. Apple (MacOS X 10.3) and FreeBSD (4.7) are very succinct in their manual pages for access(2): ``Access() is a potential security hole and should never be used.'' For naïve uses of access(2), this is true; however, we shall see that the real situation is more complicated.

2.2 Partial Solutions

We will show that the Unix system call interface, as defined, offers no completely portable, deterministic solution to the problem. The definitive solution to this problem is a kernel change, of which there are many possibilities, all of which can be made to work correctly. The simplest change would appear to be the addition of an O_RUID option to be passed to open(2), specifying that open(2) should use the real user id of the process, rather than its effective user id, for access control decisions. Without a kernel modification, two other solutions partially fix the problem.

User id juggling

Since the advent of saved user ids in 4.2BSD, through one mechanism or another, modern Unixes have had a way to temporarily drop privileges gained from a program being setuid and then later regain those privileges. Unfortunately, the setuid family of system calls is its own rats nest. On different Unix and Unix-like systems, system calls of the same name and arguments can have different semantics, including the possibility of silent failure [8]. Hence, a solution depending on user id juggling can be made to work, but is generally not portable.

Passing an open file descriptor

A somewhat improved approach is to fork off a child process, have that process permanently drop all extra privileges, and then attempt to open the file. If successful, the child process can pass the open file descriptor across a Unix-domain socket and exit.³ The user id handling is greatly simplified, although some of the caveats above still apply. The major drawback is that fork(2) is a relatively expensive system call, even with copy-on-write optimizations.

2.3 Related Work

The standard paper on this subject is the 1996 work of Bishop and Dilger [6]. They provide a very comprehensive description of the problem, dissecting a 1993 CERT advisory of a real life instance of this problem. Bishop and Dilger then go on to discuss static analysis techniques for finding the problem in C programs. Rather surprisingly, Bishop's well known 1987 paper, ``How to Write a Setuid Program'' [4] does not mention this pitfall. Bishop's book [5] also discusses the problem and its workarounds. We have tried to find the first description of this problem in the literature, but so far have come up empty.⁴ The first author recalls this problem being part of the folklore in the late 1980s.⁵

Cowan, et al., [10] cover a very similar problem, a race condition between the use of stat(2) and open(2), with their RaceGuard technology. They changed the kernel to maintain a small per-process cache of files that have been stat'd and found not to exist. If a subsequent open(2) finds an existing file, the open fails. This race condition is primarily found in the creation of temporary files. While it is essentially equivalent to the access(2)/open(2) race we consider in this paper, the solution is entirely different: they modify the kernel, we do not. Tsyrklevich and Yee [15] take a similar approach to RaceGuard, in that their solution involves a kernel modification. However, they have a richer policy language to express what race conditions they will intercept, and they suspend the putative attacker process (a process that interfered with another process' race prone call sequence) rather than causing an open(2) call to fail. Again, Tsyrklevich and Yee modify the kernel, to fix existing vulnerable applications, whereas we are proposing a user level technique to solve the problem.

3 No Deterministic Solution

Given the difficulties and overheads of existing solutions to the access(2)/open(2) race, it's tempting to try to imagine a solution that doesn't require kernel changes, juggling user ids, forking processes, or dropping privileges. Fundamentally, the problem arises because permissions to a file are a property of a path (being dependent on the relevant execute permission along all directories on the path and the relevant permissions for the filename), and the mapping of paths to files is mutable. However, the inode (and device number, and generation number if available) for a file is not a mutable mapping; it's the ground truth. Perhaps a clever combination of system calls and redundant checks, verifying that the path-to-inode mapping did not change, could be made to work, analogous to mutual exclusion protocols that don't need atomic test-and-set instructions.

A widely held belief is that such a solution isn't possible, but to our knowledge this has never been precisely stated nor proven. Here, we state and prove this theorem. Furthermore, the assumptions needed to prove the theorem will suggest an alternative solution.

Theorem 1   Under the following assumptions:

• the only way for a setuid program to determine whether the real user id should have access to a file is via the access(2) system call or other mechanisms based on the pathname (e.g., parsing the pathname and traversing the directory structures) rather than the file descriptor,
• none of the system calls for checking access permission also atomically provide a file descriptor or other unchangeable identifier of the file,
• an attacker can win all races against the setuid program,

then there is no way to write a setuid program that is secure against the access(2)/open(2) race.

The first assumption means that the theorem ignores solutions based on juggling user ids and giving up privilege, which we rule out because of portability and efficiency concerns. The first two assumptions also imply ignoring various solutions based on kernel changes: for example, an faccess(2) call that determines access permissions given a file descriptor violates the first assumption, whereas an O_RUID option to open(2), as discussed in Section 2.2, violates the second assumption. Note that although fstat(2) at first glance appears to violate the first assumption, it actually doesn't, since the stat buffer contains permission information for the file only, but doesn't consider the permissions through all directories on the file's path. In general, the theorem applies to any combination of the typical accessors of the file system state: access(2), open(2), stat(2), fstat(2), lstat(2), read(2), getdents(2), etc. The third assumption is standard when analyzing security against race conditions.

Proof: Any attempted solution will perform a sequence of system calls. We can model this sequence as a string $\sigma$ over the alphabet $\{a,o\}$, where $a$ represents a call to an access-checking function, and $o$ represents any other call, e.g., open(2). (If the attempted solution has multiple control flow paths making different sequences of calls, we can model this as a finite set of strings, one for each path through the program, and the attacker can attack each of these strings separately.) Similarly, we can model the attacker's execution as a string $\tau$ over the alphabet $\{g,b\}$, where $g$ represents swapping in a good file (one for which the real user id has permission) for the file whose access is being checked, and $b$ represents swapping in a bad file (one for which the real user id doesn't have permission). An attempted attack is an interleaving $\rho$ of the strings $\sigma$ and $\tau$.

The assumption that the attacker can win races against the setuid program means that the attacker can control what interleaving occurs (at least some fraction of the time -- we only need one success for a successful attack). Suppose the attempted solution $\sigma$ contains $n$ instances of $a$. The attack can then consist of the string $(gb)^n$, and the attacker can make the interleaving $\rho$ such that each call $a$ is immediately bracketed before by $g$ and after by $b$. Therefore, every access-checking call checks the good file and grants permission, whereas all other operations will see the same bad file, and hence there will be no inconsistencies that can be detected. Therefore, under the assumptions, there is no secure solution.

The above theorem actually generalizes to other TOCTTOU problem instances that satisfy similar assumptions. If there is no way to check something and acquire it in a single atomic operation, and if we assume the attacker can win races, then the attacker can always swap in the good thing before each check and swap in the bad thing before any other operations.

Notice how strongly the proof of the theorem relies on the assumption that the attacker can win races whenever needed. This assumption is reasonable and prudent when considering the security of ad hoc races that occurred by oversight, since a determined attacker can employ various means to increase the likelihood of winning races and can repeat the attack millions of times. However, is this assumption still reasonable if we carefully design an obstacle course of races that the attacker needs to win? By analogy to cryptology, an attacker that can guess bits of a key can break any cryptosystem, but with enough key bits, the probability of guessing them all correctly is acceptably small. This insight leads to our probabilistic solution.

4 A Probabilistic Solution

Our probabilistic solution relies on weakening the assumption that the attacker can win all races whenever needed. Instead, we will assume the more realistic assumption that, for each race, the attacker has some probability of winning. This probability will vary depending on the details of the code, the OS, the CPU speed, the disks, etc., which we will discuss in Section 5, but the fundamental idea is to treat races as probabilistic events.

The other major assumption needed for our solution is that the calls to access(2) and open(2) must be idempotent and have no undesirable side effects. For typical usages of opening files for reading or writing, this assumption is reasonable. However, one must be careful with certain usages of open(2). In particular, some common flag combinations, like (O_CREAT | O_EXCL), are not idempotent and will not work with our solution. Similarly, calling open(2) on some devices may cause undesirable side effects (like rewinding a tape), which our solution will not prevent.

The probabilistic solution starts with the standard calls to access(2) followed by open(2). However, these two calls are then followed by $k$ strengthening rounds, where $k$ is a configurable strengthening parameter. Each strengthening round consists of an additional call to access(2) followed by open(2), and then a check to verify that the file that was opened was the same as had been opened previously (by comparing inodes, etc.). When $k=0$, our solution degenerates into the standard, race-vulnerable access(2)/open(2) sequence. Figure 1 shows the code for our solution.

Figure 1: Probabilistic access(2)/open(2) Solution. For clarity, error checking and reporting code has been removed.

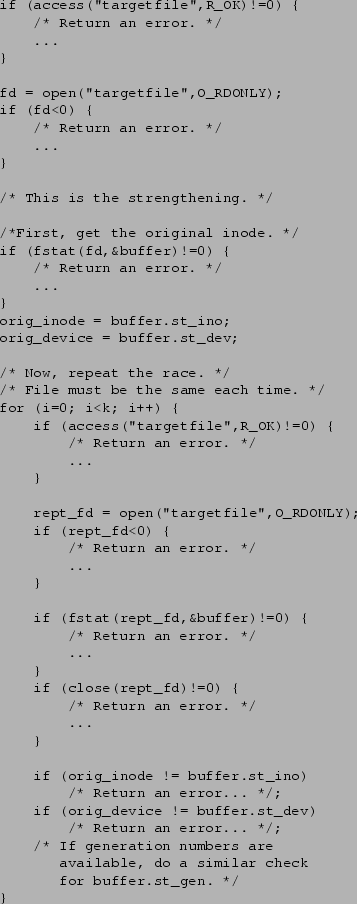The probabilistic solution adds some overhead over the simple, insecure access(2)/open(2) sequence. In particular, the runtime will grow linearly in $k$. How much improvement in security do we get for this cost in runtime?

Theorem 2   The attacker must win at least $2k+1$ races against the setuid program to break the security of our solution, where $k$ is the strengthening parameter.

Proof: Returning to the notation from the previous proof, our proposed solution is a string $\sigma$ consisting of $ao$ repeated $k+1$ times (once for the normal insecure solution, followed by $k$ rounds of strengthening). Every call $a$ to access(2) must be with a good file, or else access(2) will deny permission. Similarly, every call $o$ to open(2) must be to the same bad file, or else the verification check that all open(2) calls are for the same file will fail. Therefore, between every pair of adjacent characters in $\sigma$, the attacker must win at least one race to swap in the needed file. Since $\sigma$ is $2k+2$ characters long, there are $2k+1$ places in between characters, each requiring the attacker to win at least one race.

If we assume that each race is an independent random event with probability $p$, then the attacker succeeds with probability approximately $p^{2k+1}$. (This analysis ignores the attacks that win more than one race between characters in $\sigma$, because these will be much smaller terms for reasonable values of $p$.) Hence, the attacker must work exponentially harder as we increase $k$ linearly. This is the same trade-off behind modern cryptology.

We note that our solution should generalize to other TOCTTOU situations, provided the access check and use are side-effect free.

The assumption that each race is an independent, identically-distributed random variable is obviously not realistic. Some amount of variation or dependences in the winnability of each race does not fundamentally change our analysis: the probability of a successful attack will still be the product of $2k+1$ probabilities of winning individual races. The greatest threat is that an attacker might manage to synchronize exactly to the setuid program, so that it knows exactly when to insert its actions to win each race, making $p\approx 1$. A simple way to foil this threat is to add randomness to the delays before the access(2) and open(2) calls. We can add calls to a cryptographically strong random number generator and insert random delays into our code before each access(2) and open(2) call. The attacker would thereby have no way of knowing for sure when to win each race. On systems lacking the proc(5) file system, these delays can be calls to nanosleep(2).⁶ With the proc(5) file system, the attacker can quickly check whether the victim is running or sleeping, so the victim must always be seen to be running, even if it is only a delay loop. We note that applications implemented with user-level threads can execute code in another thread to accomplish useful work (if available) rather than simply spinning in a delay loop. Note that the stat(2) family of system calls returns time values with 1 second granularity, too coarse to be useful for the attacker. Nevertheless, despite our analysis, the only way to be certain how our solution performs in reality is to implement it and measure the results.

5 Experimental Results

We performed our experiments on the following machine configurations, where ``Ultra-60'' is a dual-processor Sun Ultra-60, and ``SS2'' is a Sun SPARCstation 2.

CPU/Clock Speed	OS	Compiler
Pentium III/500 MHz	Linux 2.4.18	GCC 2.95.3
Pentium III/500 MHz	FreeBSD 4.7	GCC 2.95.4
Ultra-60/2$\times$300 Mhz	Solaris 8	GCC 3.2
SS2/40 MHz	SunOS 4.1.4	Sun /bin/cc

For convenience, we will refer to the machines by operating system name, as these are unique. We will use the traditional terminology, where SunOS means SunOS 4.1.4, and Solaris means Solaris 8 (aka SunOS 5.8).

We developed an attack program that repeatedly forks off a copy of a victim setuid program using our strengthening, and then attempts the attack with $2k+1$ races. Figure 2 shows the core code of our attack program.

Figure 2: Attack Program Used to Measure Success Rates. We are showing only the core code, and omitting the bookkeeping and statistics-gathering. Running on the Suns required moving the DELAY1 loop to the child side of the fork.

5.1 Baseline Uniprocessor Results

As a basis for comparison, our first task was to measure how hard the classic access(2)/open(2) race is to win, in the absence of strengthening. Running on Linux and FreeBSD uniprocessors, and attacking files on the local disk, we were surprised by how hard the attack is to win. In fact, we did not observe any successful attacks in our initial experiments.⁷

Eventually, after careful tuning to match the attacker's delays to the victim as best as we could, and after extended experiments, we were able to observe some successful attacks against the $k=0$ unstrengthened access(2)/open(2) race: 14 successes out of one million trials on the 500Mhz FreeBSD box ($\sim$13hrs real time), 1 success out of 500,000 trials on the 500Mhz Linux box, and subsequently 0 successes out of an additional one million trials on the 500Mhz Linux box ($\sim$22hrs).

Some reflection suggested a possible explanation. The typical scheduling quantum on mainstream operating systems has not changed much over the past decades: on the order of tens of milliseconds. Barring any other events that cause a process to yield the CPU, a process on a uniprocessor will execute for that long quasi-atomically. However, processor speeds have increased by a few orders of magnitude over the same period, so the number of instructions that execute during a scheduling quantum from a single process has gone up accordingly. This implies that code on a uniprocessor should behave far more ``atomically'' than before and that race conditions should be far harder to win. Conversely, during the 1980s, when the access(2)/open(2) race entered the folklore, it was likely much easier to win.

To test this hypothesis, we obtained the oldest Unix-running machine we were able to resurrect sufficiently to run our experiments, a Sun SPARCstation 2 from the early 1990s. Other than conversion of function prototypes to Kernighan and Ritchie C, the code compiled and ran unmodified. On an experiment of one million attempts ($\sim$56hrs), we observed 1316 successful attacks.

The good news, then, is that on a modern uniprocessor, even the unstrengthened access(2)/open(2) race is extremely hard to win. Given the low success rate and the difficulty of tuning the attacker for $k>0$, we were never able to observe a successful attack with $k=1$.

Uniprocessor Baseline Results Summary
Machine	$k$	Attempts	Successes
Linux	0	1,500,000	1
FreeBSD	0	1,000,000	14
SunOS	0	1,000,000	1,316

5.2 Baseline Multiprocessor Results

The scheduling quantum argument does not apply, of course, to multiprocessors, so the access(2)/open(2) race should be as easy to win as ever on a multiprocessor. To test this hypothesis, we experimented with our dual-processor Solaris machine.

Against the classic $k=0$ access(2)/open(2) race, we observed 117573 successful attacks out of one million attempts. Clearly, the access(2)/open(2) race is still a major threat for multiprocessors. With the widespread introduction of multi-/hyper-threaded CPUs, this risk may exist even on ``uniprocessor'' machines.

Even with the $>$10% success rate with $k=0$, we did not feel we were able to tune the attacker for $k=1$ accurately. Intuitively, the difficulty is that we derive information for adjusting the DELAY2 and DELAY3 constants in the attacker (Figure 2) only in the cases when the $k=0$ attack would have succeeded, so little data is available for tuning. This data is swamped by other interleavings that produce indistinguishable behavior by the victim program. Out of hundreds of thousands of attempts with presumably imperfect delay tunings, there were no successful attacks with $k=1$.

Multiprocessor Baseline Results Summary
Machine	$k$	Attempts	Successes
Solaris	0	1,000,000	117,573

5.3 Measuring Strengthening

So far, we have seen that without strengthening, the access(2)/open(2) race is very hard to win on a modern uniprocessor, but easy to win on a multiprocessor. However, in either case, with even one round of strengthening, the attack success rate (observed to be 0%) is too low for us to make meaningful statements. To measure the effect of the strengthening, therefore, we need a more sensitive experiment, in which races are easier to win.

Returning to our Linux and FreeBSD uniprocessors, we inserted calls to nanosleep(2), specifying a delay of 1ns, into the setuid program. These calls have the effect of yielding the CPU at that point in the program, making the races easily winnable.

As a sanity check, we first inserted a single nanosleep(2) call after each access(2) and open(2) call in the setuid program. We then tuned the attacker with nanosleep(2) calls as well, and observed that we could attain near 100% success rates even for moderately large values of $k$. This corresponds to the case where an attacker is able to synchronize perfectly to the victim, making the probability of winning races $p\approx 1$.

Next, we randomized the delays, as described in Section 4, by changing the delay code to the following:

  nanosleep(&onenano,NULL);
  if (random() & 01)
    nanosleep(&onenano,NULL);

Note that we are using a less randomized delay than recommended in Section 4: we always have at least one nanosleep, to ensure that every race is winnable on our uniprocessors.

The table below summarizes the results for these experiments, and Figure 3 plots the data versus the theoretical model.

Strengthening with Randomized Nanosleeps
Machine	$k$	Attempts	Successes
Linux	0	100,000	99,992
Linux	1	100,000	43,479
Linux	2	100,000	16,479
Linux	3	100,000	5,931
Linux	4	100,000	1,773
Linux	5	100,000	550
FreeBSD	0	100,000	99,962
FreeBSD	1	100,000	43,495
FreeBSD	2	100,000	16,766
FreeBSD	3	100,000	5,598
FreeBSD	4	100,000	1,786
FreeBSD	5	100,000	548

Figure 3: Strengthening with Randomized Nanosleeps. The theoretical curve has been refined from $p^{2k+1}$ to $p_0 p^{2k}$, with $p_0 = 1$, because the attacker in these experiments can almost always win the first race.

Several features immediately stand out from the data. First, the almost identical numbers from Linux versus FreeBSD show that our modified code has made the probability of winning races dependent on the randomized delays, rather than on details of the respective operating systems and machines. Second, the $k=0$ numbers show that the first race is almost 100% winnable. This is because our randomized delay is at least one nanosleep long, so the attacker knows it can wait one nanosleep and always win the first race (except for rare instances when the two processes start up extremely out of sync). Finally, as $k$ grows, the ratio of successive success rates is dropping slightly. This occurs because the attacker was tuned for smaller values of $k$, and as $k$ grows, the attacker gradually slips out of phase from the victim.

As we can see, even in this extreme case, where the unstrengthened access(2)/open(2) race is almost 100% insecure and all races are constructed to be easy-to-win, each successive round of strengthening provides a multiplicative improvement in security, as predicted by the theoretical model.

Practical Guidance for Choosing $k$:

From a practical perspective, with realistic victim programs (that don't go to sleep to wait for attackers), we have observed $p$ to be on the order of $10^{-6}$ to $10^{-1}$. This suggests that for $k=7$, the probability of a successful attack should be below $10^{-15}$. Given that running one million attacks takes on the order of tens of hours, a successful attack probability of $10^{-15}$ should provide adequate security in most situations. As there are 8760 hours in a year, it is unlikely that even a cluster of 100 machines would remain running long enough to expect to see a successful attack. We note that the speed of this attack appears to be scaling with disk speed, rather than CPU speed.⁸ The relatively long duration of a trial, especially as compared to the evaluation of a hash function or block cipher, mean that we can allow a somewhat higher probability of attack than would be acceptable in other settings.

5.4 Strengthening Strengthening

Implementation details, as always, are critical to the security of a system using our algorithm. So far, we have presented a highly portable design. If one is willing to trade off portability for stronger security, a number of improvements can be made. These improvements will generally serve to decrease the possible number of context switches that could occur in the critical section, thereby decreasing worst case (real) execution time, and thereby narrowing the attacker's window. We will discuss these optimizations from most portable to least portable.

First, if the setuid program (victim) is running as root, it should raise its scheduling priority with a nice(2) or setpriority(2) call with a negative argument. This optimization appears to be completely portable.

Second, the virtual memory page(s) containing the code to implement our algorithm should be pinned into real memory. The mlock(2) call is a portable way of accomplishing this across all the operating systems discussed in this paper, although one needs to be careful to balance mlock(2) and munlock(2) calls correctly, as different operating systems have different semantics for nested calls. This optimization will prevent a page fault from occurring and giving the attacker's process a chance to run.

Third, on Linux and other systems that implement POSIX process scheduling, one can use the sched_setscheduler(2) call to elevate the process priority above what can be accomplished with nice(2) or setpriority(2). If the setuid program is running as root, it can use SCHED_FIFO with an appropriate priority to make sure that it will run whenever it is runnable.

These optimizations further reduce the probability of attack by making it harder for an attacker to win races. While the first and third optimizations would be redundant, using one of them depending on portability considerations is highly recommended. The second optimization is fairly portable, and is recommended wherever it applies.

5.5 A Note on Kernel Issues

In general, and for multiprocessor machines in particular, the probabilistic security we have achieved appears to be all that is possible: another CPU can alter the file system concurrently with the victim program's actions. However, on a uniprocessor system, we are aware of only five ways for a process to yield the CPU on most Unix-like operating systems:

• Be traced (either with ptrace(2) or through the proc(5) file system)
• Perform I/O
• Have the timer interrupt go off
• Take a page fault
• Receive a signal

We address these in order. Our discussion here is limited to the context of a setuid program running concurrently with a non-setuid program attempting to exploit the access(2)/open(2) race. This analysis explicates some of the details that are hidden by the probabilistic abstraction we have used so far.

Tracing

Either the ptrace(2) system call or the proc(5) file system provide a means to trace a process, typically for debugging purposes. One cannot trace a setuid process, as this would lead to obvious security vulnerabilities.⁹ Hence, we need not consider tracing any further.

I/O

A process yields the CPU when it needs to perform I/O operations, e.g., disk reads or writes that miss in the file system buffer cache. While the victim program is making many access(2) and open(2) calls, because of the file system buffer cache, it will be very difficult, if not impossible, for other processes to cause the inodes traversed in the access(2) call to be flushed from the buffer cache before they are traversed again by the open(2) call. In order for this to happen, another process would have to be doing I/O, which would imply that said process itself is put to sleep. One could perhaps imagine enough cooperating attack processes allocating and using lots of memory, while also all doing I/O at the same time in order to make the race condition be winnable more than once, but this would appear to be a rather difficult attack to pull off. Basically, we expect (with very high probability) that the open(2) call will never go to disk, because everything was loaded into the buffer cache by the previous access(2) call. We observe that many modern systems (e.g., FreeBSD) have unified their file system buffer caches with their virtual memory allocation. In such systems, we observe that it would be most useful to have a guaranteed minimum file system buffer cache size, so that directory entries and inodes won't be discarded from the cache to satisfy user processes' requests for memory. While many systems provide limits for number of processes per user and memory use per process, these controls are typically too coarse to be effective for bounding memory use.

Timer Interrupt

Unix-like operating systems generally implement preemptive multitasking via a timer interrupt. The frequency of the timer interrupt is generally in the range of 50-1000Hz. This frequency has not changed dramatically as CPU clock speeds have increased. We believe that this is due to the fact that human perception hasn't changed, either: if the human users are satisfied with the system's interactive latencies, it makes sense to reduce the overhead as much as possible by keeping the frequency of the timer interrupt low.

The prototypical victim program that we experimented with has 15 instructions in user mode between the actual system calls (i.e., int 0x80s) that implement access(2) and open(2), when using GCC 2.95.3 and glibc 2.2.5. The time required to execute the 15 user mode instructions has, of course, decreased dramatically as CPU speeds have increased. This helps prevent the exploitation of the race in two ways: first, it gives the timer interrupt an ever shrinking window of time to occur in, and second, the victim program will be able to run at least one round of the strengthening protocol without interference from the timer interrupt.

Page Faults

If we assume that our algorithm is running as the superuser (e.g., a setuid root program), then the program can call mlock(2) to pin the page containing the code into memory, so it will never take a page fault. Processes not running as root cannot take advantage of page pinning on systems the authors are familiar with.

Signals

The last way of causing a process to yield the CPU is to have a signal delivered to it. Again, on all the Unix-like operating systems the authors are familiar with, signal delivery is handled at the point that the operating system is about to return to user mode, either from a system call, or an interrupt, such as the timer interrupt. We note that on Linux 2.4.18, the code for posting a signal to a process includes logic that dequeues a pending SIGCONT (and equivalents) if a SIGSTOP (or equivalent) signal is being delivered, and vice versa. This implies that the attacker cannot use signals to single-step the victim through system calls. The attacker can stop and restart the victim program at most once due to the length of scheduling quanta. A similar result is true of the timer interrupt: given the size of the scheduling quantum, all of the code will execute as part of at most 2 scheduling quanta. So again, the attacker gets 1 chance to change the file system around, but they need at least 3 changes to the file system to succeed against 1 round of strengthening.

Observation

In summary, it appears that Linux 2.4.18, when running on modern uniprocessor machines, and with the victim program having superuser privileges, can provide more security than one would assume from the model and experiments presented above. That is, with one round of strengthening, the attacker must make three sets of modifications to the file system to succeed with an attack, but the timer interrupt will only give the attacker one chance to run. Linux's signal handling behavior prevents the attacker from single-stepping the victim at system call granularity.

This analysis appears to support a conjecture that on Linux 2.4.18, running as root (and therefore able to use SCHED_FIFO and mlock(2), uniprocessor machines achieve deterministic security with only one round of strengthening. While this analysis is intellectually interesting, we strongly urge that it not be used, as it depends on code never being run on a multiprocessor (very difficult to ensure as systems evolve over time), and undocumented behavior of a particular kernel version, which is always subject to change.

6 Conclusion

The race condition preventing the intended use of the access(2) system call has existed since 1979. To date, the only real advice on the matter has been ``don't use access.'' This is unfortunate, as it provides useful functionality. We have presented an algorithm that gains exponential advantage against the attacker while doing only linear work. This is the same sort of security as modern cryptology gives, although we use arguably simpler assumptions. We note that either a probabilistic solution as presented in this paper or dropping privilege via setuid(2) are fundamentally the only viable solutions if one is unwilling or unable to alter the kernel. The way Linux handles pending SIGSTOP and SIGCONT signals provides additional security against TOCTTOU attacks. Other kernels should investigate adding similar code to their signal posting routines, although this is not a completely general solution - multiprocessor machines inherently can achieve only a probabilistic guarantee. With appropriate parameter choices, this algorithm, within its limitations regarding side effects, restores the access(2) system call to the toolbox available to the developer of setuid Unix programs.

Acknowledgments

We wish to thank Whitfield Diffie for access to old Sun hardware. The staff (and stock) of Weird Stuff Electronics¹⁰ was very helpful as well. We thank Steven Bellovin, Brian Kernighan, Nancy Mintz, Dennis Ritchie, and Jonathan Shapiro for historical information about the access(2)/open(2) race. We thank the anonymous referees for helpful feedback on an earlier draft of this paper. Drew Dean wishes to acknowledge a conversation with Dirk Balfanz, Ed Felten, and Dan Wallach on the beach at SOSP '99 that firmly planted this problem in his mind, though the solution presented in this paper was still years away.

Bibliography

1

Aleph1.
Smashing the stack for fun and profit.
Phrack #49, November 1996.
https://www.phrack.org/show.php?p=49&a=14.

2

Steven M. Bellovin.
Shifting the odds: Writing (more) secure software.
https://www.research.att.com/~smb/talks/odds.pdf, December 1994.

3

Sandeep Bhatkar, Daniel C. DuVarney, and R. Sekar.
Address obfuscation: An efficient approach to combat a broad range of memory error exploits.
In Proceedings of the 12th USENIX Security Symposium, pages 105-120, Washington, DC, August 2003.

4

Matt Bishop.
How to write a setuid program.
;login:, 12(1):5-11, 1987.

5

Matt Bishop.
Computer Security: Art and Science.
Addison-Wesley, 2003.

6

Matt Bishop and Michael Dilger.
Checking for race conditions in file accesses.
Computing Systems, 9(2):131-152, Spring 1996.

7

CERT Coordination Center.
xterm logging vulnerability.
CERT Advisory CA-1993-17, October 1995.
https://www.cert.org/advisories/CA-1993-17.html.

8

Hao Chen, David Wagner, and Drew Dean.
Setuid demystified.
In Proceedings of the Eleventh Usenix Security Symposium, San Francisco, CA, 2002.

9

Crispan Cowan, Calton Pu, Dave Maier, Jonathan Walpole, Peat Bakke, Steve Beattie, Aaron Grier, Perry Wagle, Qian Zhang, and Heather Hinton.
StackGuard: Automatic adaptive detection and prevention of buffer-overflow attacks.
In Proc. 7th USENIX Security Conference, pages 63-78, San Antonio, Texas, January 1998.

10

Crispin Cowan, Steve Beattie, Chris Wright, and Greg Kroah-Hartman.
RaceGuard: Kernel protection from temporary file race vulnerabilities.
In Proceedings of the 10th USENIX Security Symposium, Washington, DC, August 2001.

11

W. S. McPhee.
Operating system integrity in OS/VS2.
IBM Systems Journal, 13(3):230-252, 1974.

12

Greg Morrisett, David Walker, Karl Crary, and Neal Glew.
From system F to typed assembly language.
ACM Transactions on Programming Languages and Systems, 21(3):527-568, May 1999.

13

George C. Necula.
Proof-carrying code.
In Proceedings of the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, pages 106-119, January 1997.

14

Thomas Toth and Christopher Kruegel.
Accurate buffer overflow detection via abstract payload execution.
In Andreas Wespi, Giovanni Vigna, and Luca Deri, editors, Proceedings Fifth Symposium on Recent Advances in Intrusion Detection, volume 2516 of LNCS, pages 274-291, Zurich, Switzerland, October 2002. Springer-Verlag.

15

Eugene Tsyrklevich and Bennet Yee.
Dynamic detection and prevention of race conditions in file accesses.
In Proceedings of the 12th USENIX Security Symposium, pages 243-256, Washington, DC, August 2003.

16

A. C. Yao.
Theory and application of trapdoor functions.
In Proc. $23$rd IEEE Symp. on Foundations of Comp. Science, pages 80-91, Chicago, 1982. IEEE.

Footnotes

... Dean¹

Work supported by the Office of Naval Research under contract N00014-02-1-0109. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Office of Naval Research.

... Hu²

Work done mostly while a Visiting Fellow at SRI. Supported in part by a grant from the Natural Science and Engineering Research Council of Canada.

... exit.³

This idea was communicated to the first author by Michael Plass of PARC.

... empty.⁴

We would greatly appreciate any citation between 1979 and 1992 being brought to our attention.

... 1980s.⁵

Messrs. Bellovin, Kernighan, Ritchie, Shapiro and Ms. Mintz concur with this recollection in private communication, January 2004.

...nanosleep(2).⁶

For our purposes, nanosleep(2) can be implemented (on systems where it is not natively available) by calling select(2) with the smallest, non-zero timeout, and empty sets of file descriptors to watch.

... experiments.⁷

We did run some limited experiments attacking files across NFS and observed substantial numbers of successes. We chose not to continue these experiments, however, because NFS-accessed files are usually not the most security-critical, root privileges typically don't extend across NFS, the data displayed enormous variance depending on network and fileserver load, and both authors felt that continuously attacking their respective fileservers for days on end would be considered anti-social by our colleagues.

... speed.⁸

We heard disk drives grinding away during our experiments.

... vulnerabilities.⁹

At least in theory. Various vulnerabilities in this area have been found over the years in different kernels. However, such kernel vulnerabilities directly lead to machine compromise regardless of the access(2)/open(2) race.

... Electronics¹⁰

https://www.weirdstuff.com