 |

 |
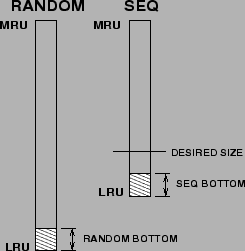
We shall develop an adaptive, self-tuning, low overhead algorithm that dynamically partitions the amount of cache space amongst sequential and random data so as to minimize the overall miss rate. Given the radically different nature of sequentially prefetched pages and the random data, it is natural to separate these two types of data. As shown in Figure 2, we will manage each class in separate LRU lists: RANDOM and SEQ. One of our goals is to avoid thrashing [34] that happens when more precious demand-paged random pages are replaced with less precious prefetched pages (cache pollution) or when prefetched pages are replaced too early before they are used.
A key idea in our algorithm is to maintain a desired size (see Figure 2) for SEQ list. The tracks are evicted from the LRU end of SEQ, if its size (in pages) is larger than the desired size; otherwise, the tracks are evicted from the LRU end of RANDOM. The desired size is continuously adapted. We now explain the intuition behind this adaptation.
Assuming that both the lists satisfy the LRU stack property (see Section II-C), the optimum partition is one that equalizes the marginal utility of allocating additional cache space to each list. We design a locally adaptive algorithm that starts from any given cache partitioning and gradually and dynamically tweaks it to gear it towards the optimum. As an important step towards this goal, we first derive an elegant analytical model for computing the marginal utility of allocating additional cache space to sequentially prefetched data. In other words, how does the number of sequential misses experienced by SEQ change as the size of the list changes. Similarly, as a second step, we empirically estimate the marginal utility of allocating additional cache space to random data. Finally, as the third step, if during a certain time interval the marginal utility of SEQ list is higher than that of RANDOM list, then the desired size is increased; otherwise, the desired size in decreased.