data blocking.

Blocking is an optimization technique that allows a full cache use and thus reduces memory bandwidth usage. Blocking is no always possible: for BLAS 1 and 2 the majority of data is accessed only one time making temporal locality very low; on the other hand Level 3 operations use a three nested loop structure with 2 dimension matrices making each matrix elements accessed more than on time. We give an example for matrix matrix product C = A.B where C, A and B are respectively m x n, m x p and p x n matrices; in this case each element of A and B are accessed respectively n and m times. The block method for matrix matrix product generally consist of:

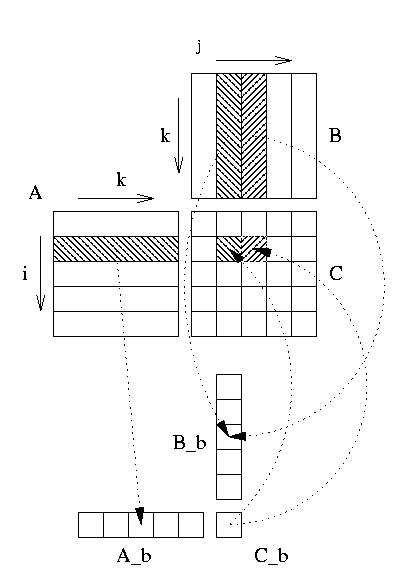
• split result matrix C into blocks C_i,j of size n_b x n_b, each blocks is constructed into a continuous array C_b which is then copied back into the right C_i,j.
• matrices A and B are split into panels A_i and B_j of size n_b x m and k x n_b each panel is copied into continuous arrays A_b and B_b. The choice of n_b must ensure that C_b A_b and B_b fit into one level of cache, usually L2 cache.

then:

We suppose for simplicity that n_b divides m, n and p. Figure  may help in understanding operations performed on blocks. In the case of the previous algorithm matrix A is loaded only one time into cache compared to the n times access of a classical ijk loop while matrix B is still accessed m times. This simple block method greatly reduce memory access and real codes may choose by looking at matrix size which loop structure (ijk vs. jik) is best appropriate and if some matrix operand fits totally into cache.

In the previous we where working on L2 cache and we does no talk about L1 cache use. In fact L1 will be generally too small to handle a C_i,j block and one panel of A and B but remember that operation performed at step 7 of the previous algorithm is a matrix matrix product so each operand A_bk and B_bk is accessed n_b times: this part could also use a block method. Since n_b is relatively small the implementation may load only one of C_b, A_bk, B_bk into L1 cache and works with others from L2 cache. The reader may refer to ATLAS source code and description for a complete analysis and test of block methods in various environments. Another projects for fast matrix matrix multiply are Phipac¹³[6] and the BLAIS[7] library from MTL¹⁴.

Figure: Block matrix matrix product.