Coins and cryptographic terminology

  An e-coin (coin for short) is an object consisting of a unique identifier (serial number, counter) called the coin ID, an indication of value (denomination), an expiry date, and an authenticating cryptographic tag. This cryptographic tag can be implemented in different ways. In our design we choose to use a MAC, or message authentication code, on the rest of the information, computed using a symmetric key which is kept in secret by the issuer. Thus, the issuer can compute and verify the tag, but no other party can compute a valid tag. Because it is secret-key based, the tag cannot even be checked by anyone except the issuer, i.e., this is not a digital signature. This is done for efficiency reasons--symmetric key based cryptography is hundreds of times more efficient than public-key operations. A schematic representation of a coin is shown in Figure 1.

 

Figure 1:   Structure of an un-encrypted coin.

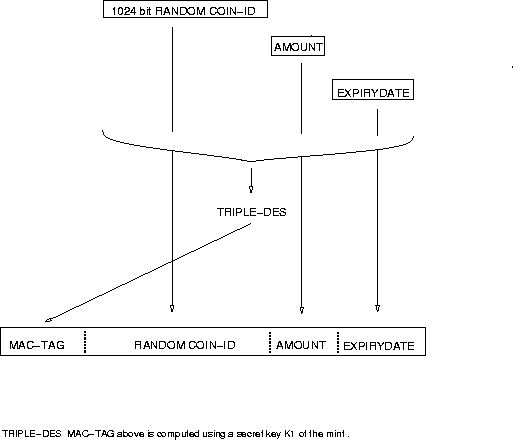
The cost of successful tag forgery can be enormous, since if an adversary could forge tags, he or she could manufacture counterfeit coins at will. In order to minimize the possibility of successful tag forgery, we suggest the following:

• First, the tag should be computed in protected, tamper-proof hardware. This minimizes the risk of loss of the secret key.
• Second, the tag-computing algorithm should be ``strong.'' One can of course use MACs based on existing primitives such as DES. This may be acceptable, but we suggest that a Triple-DES based MAC be used. A good choice would be a Wegman-Carter [23] type MAC, meaning that one applies an XOR-universal hash function to the data and then XORs the result with the value of a Triple-DES based pseudorandom function applied to a counter. The size of each tag should be (at least) 128 bits, so the total tag length is 28 bytes. Outside the cryptographic module the tag is encrypted inside the issuer database, and it goes encrypted over the network. It is only available in plain form to the receiver of the coin.

Additional protection is provided by the fact that the coin database itself is protected. So that if an adversary manages to forge the correct tag for a coin which has not yet been issued, it will not help, because the issuer will fail to validate the coin. Thus, the adversary must be able to successfully forge tags of issued, un-spent coins to achieve a meaningful gain.

A coin can have various states. For example, spent or not; anonymous or not; split, and if so how; etc. These are marked in the database.

The issuer will expect from a coin purchaser requesting coins, or a change maker wanting change, a specification of exactly what kinds of coins are being requested. The specification takes the form of a list of denominations, and for each denomination, the number of coins of that denomination that is desired. The simplest thing is to just ask for one coin of a certain denomination, for example a single coin of $0.80. But one could ask for, say, $(2,\$2.50),(1,\$1.25),(3,\$2)$,meaning I want 2 coins of value $2.50 each, one coin of value $1.25, and 3 coins of value $2. The total value of the list is the total dollar value, $12.25 in the example just given. The choice of specification is decided by a combination of the user's needs and the software (purse).

  

Figure 2: Keys and cryptographic primitives used in protocols

The cryptographic primitives used in the protocols of Section 3 are summarized in Figure 2. All the parties have public keys. The issuer has a cache of identities and their corresponding public keys, so that the certification authority is not needed in transactions with the issuer. (But it may be needed for other transactions.)

The encryption function $\mbox{\bf E}^*_{X}$ must provide, besides secrecy, some form of ``message integrity.'' Decryption of a ciphertext results either in a plaintext message, or in a flag indicating non-validity. Formally, the property we require of the encryption scheme is plaintext awareness [5,2]. Roughly speaking, this means that correct decryption convinces the decryptor that the transmitter ``knows'' the plaintext that was encrypted. This is the strongest known type of security, and in particular it is shown in [2] that it implies non-malleability (it is not possible to modify a ciphertext in such a way that the resulting plaintext is meaningfully related to the original one, as formalized in [11]) and security against chosen-ciphertext attacks. A simple, efficient scheme to achieve such encryption using RSA is OAEP [5]. A Diffie-Hellman based solution can be found in [1]. (Note that the RSA PKCS #1 encryption standard can be broken under chosen ciphertext attacks [6], and is thus not suitable for our purposes.)

However we stress that plaintext-aware encryption does not provide authentication in the manner of a signature, i.e., it does not provide non-repudiation. But it prevents an adversary from tampering with a ciphertext.

Also note that the encryption function is randomized: $\mbox{\bf E}^*$, invoked upon message m will use, to compute its output, some randomizer, so that each encryption is different from previous ones.

Finally, the notation $\oplus$ denotes bitwise XOR.