7th USENIX Security Symposium, 1998
[Technical Program]
| Pp. 201–216 of the Proceedings |  |
Finite-State Analysis of SSL 3.0
John C. Mitchell, Vitaly Shmatikov, and Ulrich Stern
Computer Science Department
Stanford University
Stanford, CA 94305
{jcm,shmat,uli}@cs.stanford.edu
Abstract
The Secure Sockets Layer (SSL) protocol is analyzed using a
finite-state enumeration tool called Mur .
The analysis is presented using a sequence of incremental
approximations to the SSL 3.0 handshake protocol.
Each simplified protocol is ``model-checked'' using Mur ,
with the next protocol in the sequence obtained by correcting
errors that Mur finds automatically.
This process identifies the main shortcomings in SSL 2.0
that led to the design of SSL 3.0, as well as a few anomalies
in the protocol that is used to resume a session in SSL 3.0.
In addition to some insight into SSL, this study demonstrates
the feasibility of using formal methods to analyze commercial protocols.
In previous work [9], a general-purpose finite-state analysis
tool has been successfully applied to the verification of small security
protocols such as the Needham-Schroeder public key protocol, Kerberos,
and the TMN cellular telephone protocol. The tool,
Mur [3, 10], was designed for hardware verification
and related analysis. In an effort to understand the difficulties
involved in analyzing larger and more complex protocols, we use Mur
to analyze the SSL 3.0 handshake protocol. This protocol is important,
since it is the de facto standard for secure Internet communication,
and a challenge, since it has more steps and greater complexity than the
other security
protocols analyzed using automated finite-state exploration. In
addition to demonstrating that finite-state analysis is feasible for
protocols of this complexity, our study also points to several anomalies
in SSL 3.0. However, we have not demonstrated the possibility of
compromising sensitive data in any implementation of the protocol.
In the process of analyzing SSL 3.0, we have developed a ``rational
reconstruction'' of the protocol. More specifically, after initially
attempting to familiarize ourselves with the handshake protocol, we
found that we could not easily identify the purpose of each part of
certain messages. Therefore, we set out to use our analysis tool to
identify, for each message field, an attack that could arise if that
field were omitted from the protocol. Arranging the simplified
protocols in the order of increasing complexity, we obtain an
incremental presentation of SSL. Beginning with a simple, intuitive, and
insecure exchange of the required data, we progressively introduce
signatures, hashed data, and additional messages,
culminating in a close approximation of the
actual SSL 3.0 handshake protocol.
In addition to allowing us to understand the protocol more fully
in a relatively short period of time, this incremental reconstruction
also provides some evidence for the ``completeness" of our
analysis. Specifically, Mur exhaustively tests all possible
interleavings of protocol and intruder actions, making sure that
a set of correctness conditions is satisfied in all cases.
It is easy for such analysis to be ``incomplete" by not
checking all of the correctness conditions intended by the
protocol designers or users. In developing our incremental
reconstruction of SSL 3.0, we were forced to
confirm the importance of each part of each message.
In addition, since no formal or high-level description of SSL 3.0
was available, we believe that the description of SSL 3.0
that we extracted from the Internet Draft [6]
may be of interest.
Our analysis covers both the standard handshake protocol
used to initiate a secure session
and the shorter protocol used to resume a session [6, Section 5.5,].
Mur analysis uncovered a weak form of version rollback attack
(see Section 4.9.2) that can cause a version 3.0 client and
a version 3.0 server to commit to SSL 2.0 when the protocol is resumed.
Another attack on the resumption protocol (described in
Sections 4.8 and 4.9.1)
is possible in SSL implementations that strictly follow the Internet draft [6]
and allow the participants to send application data without waiting
for an acknowledgment of their Finished messages.
Finally, an attack on cryptographic preferences (see Section 4.6)
succeeds if the participants support weak encryption
algorithms which can be broken in real time.
Apart from these three anomalies, we were not able to uncover any
errors in our final protocol.
Since SSL 3.0 was designed to be backward-compatible, we also
implemented and checked a full model for SSL 2.0 as part of the SSL 3.0 project.
In the process, Mur uncovered the major
problems with SSL 2.0 that motivated the design of SSL 3.0.
Our Mur analysis of SSL is based on the assumption that
cryptographic functions cannot be broken.
For this and other reasons (discussed below), we cannot
claim that we found all attacks on SSL. But our analysis
has been efficient in helping discover an important
class of attacks.
The two prior analyses of SSL 3.0 that we are aware of are
an informal assessment carried out by Wagner and Schneier [14]
and a formal analysis by Dietrich using a form of belief logic [2].
(We read the Wagner and Schneier study before carrying out our analysis,
but did not become aware of the Dietrich study until after we had
completed the bulk of our work.)
Wagner and Schneier comment on the possibility of anomalies associated
with resumption, which led us to concentrate our later efforts on
this area. It is not clear to us at the time of this writing whether
we found any resumption anomalies that were not known to these
investigators. However, in email comments resulting from circulation
of an earlier document [13], we learned that while
our second anomaly was not noticed by Wagner and Schneier, it was
later reported to them by Michael Wiener.
Neither anomaly seems to have turned up in
the logic-based study of [2].
A preliminary report on this study was presented in a panel
at the September 1997 DIMACS Workshop on
Design and Formal Verification of Security Protocols and appears
on the web site (https://dimacs.rutgers.edu/Workshops/Security/)
and CD ROM associated with this workshop.
Our study of resumption was carried out after
our workshop submission and is not described in the workshop document.
Our general methodology for modeling security protocols
in Mur is described in our previous paper [9],
and will be only outlined in this section.
The basic approach is similar to the CSP approach to
model checking of cryptographic protocols
described in [8, 11].
Mur [3] is a
protocol or, more generally, finite-state machine
verification tool. It has been successfully
applied to several industrial protocols, especially in the
domains of multiprocessor cache coherence protocols and
multiprocessor memory models [4, 12, 15].
The purpose of finite-state analysis, commonly called
``model checking,'' is to exhaustively search all
execution sequences. While this process often reveals
errors, failure to find errors does not imply that
the protocol is completely correct, because the
Mur model may simplify certain details and
is inherently limited to configurations involving a
small number of, say, clients and servers.
To use Mur for verification, one has to model the protocol
in the Mur language and augment this model with a
specification of the desired properties. The Mur system
automatically checks, by explicit state enumeration, if all
reachable states of the model satisfy the given specification.
For the state enumeration,
either breadth-first or depth-first search
can be selected. Reached states are stored in a hash
table to avoid redundant work when a state is revisited.
The memory available for this hash table typically determines
the largest tractable problem.
The Mur language is a simple high-level language for describing
nondeterministic finite-state machines.
Many features of the language
are familiar from conventional programming languages.
The main features not found in a
``typical'' high-level language are described in the following
paragraphs.
The state of the model
consists of the values of all global
variables. In a startstate statement, initial values are assigned to
global variables. The transition from one state to another is
performed by rules. Each rule has a Boolean condition and an
action, which is a program segment that is executed atomically.
The action may be executed if the condition is true
(i.e., the rule is enabled) and typically changes
global variables, yielding a new state.
Most Mur models are nondeterministic
since states typically allow execution of more
than one rule.
For example, in the model of the SSL protocol,
the intruder (which is part of the model) usually
has the nondeterministic choice of several messages
to replay.
Mur has no explicit notion of processes. Nevertheless
a process can be implicitly modeled by a set of related rules.
The parallel composition of two processes
in Mur is simply done by using the union of the rules of
the two processes.
Each
process can take any number of steps (actions) between the
steps of the other. The resulting computational model is that
of asynchronous, interleaving concurrency.
Parallel processes communicate
via shared variables; there are no special language constructs
for communication.
The Mur language supports scalable models.
In a scalable model,
one is able to change the size of the model by
simply changing constant declarations.
When developing protocols, one typically starts
with a small protocol configuration. Once this
configuration is correct, one gradually increases the protocol
size to the largest value that still allows verification to complete.
In many cases, an error in the general (possibly infinite state)
protocol will also show up in a down-scaled (finite state)
version of the protocol. Mur can only
guarantee correctness of the down-scaled version of the protocol,
but not correctness of the general protocol.
For example, in the model of the SSL protocol, the numbers of clients and
servers are scalable and defined by constants.
The desired properties of a protocol can be specified in
Mur by
invariants, which are Boolean conditions that have to be true
in every reachable state.
If a state is reached in which some invariant is violated,
Mur prints
an error trace - a sequence of states from the start state
to the state exhibiting the problem.
In outline, we have analyzed protocols using the following sequence of
steps:
- Formulate the protocol. This generally involves simplifying
the protocol by identifying the key steps and primitives. The
Mur formulation of a protocol, however,
is more detailed than the high-level
descriptions often seen in the literature,
since one has to decide exactly which
messages will be accepted by each participant in the protocol.
Since Mur communication is based on shared variables,
it is also necessary to define an explicit message format,
as a Mur type.
- Add an adversary to the system. We generally assume
that the adversary (or intruder) can masquerade as
an honest participant in the system, capable of
initiating communication with a truly honest participant, for example.
We also assume that the network is under control of the adversary
and allow the adversary the following actions:
- overhear every message, remember all parts of each message,
and decrypt ciphertext when it has the key,
- intercept (delete) messages,
- generate messages using any combination of initial knowledge
about the system and parts of overheard messages.
Although it is simplest to formulate an adversary that nondeterministically
chooses between all possible actions at every step of the protocol,
it is more efficient to reduce the choices to those that actually
have a chance of affecting other participants. - State the desired correctness condition.
A typical correctness criterion includes, e.g., that
no secret information can be learned by the intruder.
More details about the correctness criterion used for
our SSL model are given in Section 3.
- Run the protocol for some specific choice of system
size parameters. Speaking very loosely, systems with 4 or 5 participants
(including the adversary) and 5 to 7 intended steps in the original
protocol (without adversary) are easily analyzed in
minutes of computation time using a modest workstation.
Doubling or tripling these numbers, however, may cause the system
to run for many hours, or terminate inconclusively by
exceeding available memory.
- Experiment with alternate formulations and repeat.
This is discussed in detail in Section 4.
The intruder model described above
is limited in its
capabilities and does not have all the power that a real-life intruder
may have.
In the following, we discuss examples of these limitations.
Our intruder ignores both computational and number-theoretic properties
of cryptographic functions. As a result, it cannot perform any
cryptanalysis whatsoever. If it has the proper key, it can read an
encrypted message (or forge a signature). Otherwise, the only action it
can perform is to store the message for a later replay. We do not model
any cryptographic attacks such as brute-force key search (with a related
notion of computational time required to attack the encryption) or
attacks relying on the mathematical properties of cryptographic
functions.
Mur has no notion of probability. Therefore, we do not model
``propagation'' of attack probabilities through our finite-state system
(e.g, how the probabilities of breaking the encryption, forging the
signature, etc. accumulate as the protocol progresses). We also ignore,
e.g., that the intruder may learn some probabilistic information
about the participants' keys by observing multiple runs of the protocol.
Keys, nonces, etc. are treated as atomic entities in our model. Our
intruder cannot break such data into separate bits. It also cannot perform
an attack that results in the partial recovery of a secret (e.g., half
of the secret bits).
In spite of the above limitations, we believe that Mur is a useful
tool for analyzing security protocols. It considers the protocol
at a high level and helps discover a certain class of bugs that do not
involve attacks on cryptographic functions employed in the protocol. For
example, Mur is useful for discovering ``authentication'' bugs,
where the assumptions about key ownership, source of messages, etc. are
implicit in the protocol but never verified as part of the message
exchange. Also, Mur models can successfully discover attacks on
plaintext information (such as version rollback attacks in SSL) and
implicit assumptions about message sequence in the protocol (such as
unacknowledged receipt of Finished messages in SSL).
Other examples of errors discovered by finite-state analysis
appear in [8, 9, 11] and in references cited
in these papers.
The primary goal of the SSL 3.0 handshake protocol is to establish
secret keys that ``provide privacy and reliability between two
communicating applications'' [6]. Henceforth, we call the
communicating applications the client (C) and the server (S). The
basic approach taken by SSL is to have C generate a fresh random
number (the secret or shared secret)
and deliver it to S in a secure manner.
The secret is then used to compute a so-called master secret
(or negotiated cipher), from which, in turn,
the keys that protect and authenticate subsequent
communication between C and S are computed.
While the SSL handshake protocol
governs the secret key computation,
the SSL record layer protocol governs the subsequent secure
communication between C and S.
As part of the handshake protocol, C and S exchange their respective
cryptographic preferences, which are used to select a mutually
acceptable set of algorithms for encrypting and signing handshake
messages. In our analysis, we assume for simplicity that RSA is used for both
encryption and signatures, and cryptographic preferences only indicate
the desired lengths of keys. In addition, SSL 3.0 is designed to be
backward-compatible so that a 3.0 server can communicate with a
2.0 client
and vice versa. Therefore, the parties also exchange their respective
version numbers.
The basic handshake protocol consists of three messages. With the
ClientHello message, the client starts the protocol
and transmits its version number and cryptographic preferences
to the server. The server replies with the ServerHello
message, also transmitting its version number and cryptographic
preferences. Upon receipt of this message, the client
generates the shared secret and sends it securely to the server in
the secret exchange message.
Since we were not aware of any formal definition of SSL 3.0, we based
our model of the handshake protocol on
the Internet draft [6]. The
draft does not include a precise list of requirements that must be
satisfied by the communication channel created after the handshake
protocol completes. Based on our interpretation of the informal
discussion in Sections 1 and 5.5 of the Internet draft,
we believe that the resulting channel
can be considered ``secure'' if and only if
the following properties hold:
We propose that any violation of the foregoing invariants that goes
undetected by the legitimate participants constitutes a successful
attack on the protocol.
SSL 3.0 supports protocol resumption. In the initial run of the
protocol, C and S establish a shared secret by going through the
full protocol and computing secret keys that protect subsequent communication.
SSL 3.0 allows the parties to resume
their connection at a later time without repeating the full protocol.
If the ClientHello message
sent by C to S includes the identifier of an SSL
session that is still active according to S's internal state,
S assumes that C wants to resume a previous session. No new
secret is exchanged in this case, but the master secret and
the keys derived from it are recomputed using new nonces. (See Section
4.8 for an explanation of how nonces are used in the protocol to
prevent replay attacks, and Appendix B to see how the
master secret is computed from the nonces and shared secret.) Our
Mur model supports protocol resumption.
Finally, it should be noted that whenever one of the parties detects an
inconsistency in the messages it receives, or any of the protocol steps
fails in transmission, the protocol is aborted and the parties revert to
their initial state. This implies that SSL is susceptible by design to
some forms of ``denial of service'' attacks: an intruder can simply
send an arbitrary message to a client or server engaged in the handshake protocol,
forcing protocol failure.
We start our incremental analysis with the simplest and most intuitive
version of the protocol and give an attack found by Mur . We then add
a little piece of SSL 3.0 that foils the attack, and let Mur discover
an attack on the augmented protocol. We continue this iterative process
until no more attacks can be found. The final protocol
closely resembles SSL 3.0, with some simplifications
that result from our assumption of perfect cryptography (see below).
The following notation will be used throughout the paper.
In general, our model assumes perfect cryptography. The following list
explains what this assumption implies for all cryptographic functions
used in SSL.
- Opaque encryption.
-
Encryption is assumed to be opaque. If a message has the form
 , only party i can learn x. (This is only
true iff the private key  is not available to any party except
i. This is a safe assumption, given that no participants in the SSL
handshake protocol are ever required to send their private key over the
network.) The intruder may, however, store the entire encrypted message
and replay it later without learning x. The structure of the
encrypted message is inaccessible to the intruder, i.e., it cannot split
the encrypted message into parts and insert them into other encrypted
messages.
- Unforgeable signatures.
-
Signatures are assumed to be unforgeable. Messages of the form
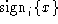 can only be generated by the
party i. Anyone who possesses i's verification key  is able to
verify that the message was indeed signed by i. We assume that
signatures do not encrypt. Therefore, x can be learned by anyone.
- Hashes.
-
Hashes are assumed to be preimage resistant and
2nd-preimage resistant: given a message of the form
 , it is not computationally feasible to
discover x, nor find any x' such that
 .
It is therefore assumed that
a participant can determine whether x=x' by
comparing to
 .
- Trusted certificate authority.
-
There exists a trusted certificate authority (CA). All parties
are assumed to possess CA's verification key
 ,
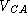and are thus able to verify messages signed by CA. Every party
i is assumed to possess CA-signed certificates for its own
public keys: 
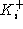(certifying that public encryption key  indeed belongs to i)
and 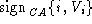 (certifying that
public verification key indeed belongs to i).
The first step of the basic protocol consists of C sending information
about its identity, SSL version number, and cryptographic preferences
(aka cryptosuite) to S. Upon receipt of C's Hello message,
S sends back its version, cryptosuite (S selects one set of
algorithms from the preference list submitted by C), and its public
encryption key. C then generates a random secret and sends it to S,
encrypted by S's public key.
Notice that the first Hello message (that from C to S) contains the
identity of C. There is no way for S to know who initiated the
protocol unless this information is contained in the message itself
(perhaps implicitly in the network packet header).
Protocol A does not explicitly (and securely)
associate the server's name with
its public encryption key. This allows the intruder to insert its own
key into the server's Hello message. The client then encrypts the
generated secret with the intruder's key, enabling the intruder to read
the message and learn the secret.
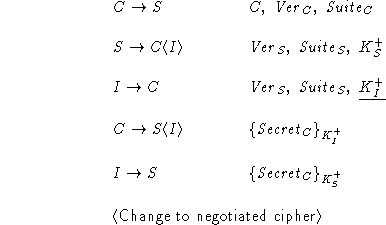
To fix the bug in Protocol A, we add verification
of the public key.
The server now sends its public key  in a
certificate signed by the certificate authority. As
described before, the certificate has the following form:
 .
We assume that signatures are unforgeable. Therefore, the intruder will
not be able to generate  . The intruder may send the certificate for its own public key
 , but the client
will reject it since it expects S's name in the certificate. Finally,
the intruder may generate  , but the client expects a message signed by CA, and
will try to verify it using CA's verification key. Verification
will fail since the message is not signed by CA, and the client
will abort the protocol. Notice that SSL's usage of certificates to
verify the server's public key depends on the trusted certificate authority
assumption (see Section 4.2 above).
Protocol B includes no verification of the
client's identity. This allows
the intruder to impersonate the client by generating protocol messages
and pretending they originate from C. In particular, the intruder is
able to send its own secret to the server, which the latter will use to
compute the master secret and the derived keys.
To fix the bug in Protocol B, the server has to verify that the
secret it received was indeed generated by the party whose identity was
specified in the first Hello message. For this purpose, SSL employs
client signatures.
The client sends to the server its verification key in the
CA-signed certificate  . In addition, immediately after sending its secret
encrypted with
the server's public key, the client signs the hash of the secret
 and sends it to the
server. Hashing the secret is necessary so that the intruder will not
be able to learn the secret even if it intercepts the message. Since
the server can learn the secret by decrypting the client key exchange
message, it is able to compute the hash of the secret and compare it
with the one sent by the client.
Notice that the server can be assured that  is indeed C's
verification key since the intruder cannot insert its own key in the
CA-signed certificate assuming that signatures are unforgeable. Therefore, the server
will always use to verify messages ostensibly signed by the
client, and all messages of the form  will be rejected. Even if the intruder were able to generate
the message  , the attack
will be detected when the server computes  and discovers
that it is different from  .
Instead of signing the hashed secret, the client can sign the secret
directly and send it to the server encrypted by the server's public key.
The SSL definition, however, does not include encryption in this step
[6, Section 5.6.8,]. We used hashing instead of encryption as
well since we intend our incremental reconstruction of SSL to follow the
definition as closely as possible. One of the anonymous reviewers
suggested that hashing is used instead of encryption so that
the encrypted part of the message
(i.e., a secret as opposed to a signed secret)
fits within the modulus size of the server's encryption function.
Even though the intruder can modify neither keys nor shared secret in
Protocol C, it is able to attack the plaintext information
transmitted in the Hello messages. This includes the parties' version
numbers and cryptographic preferences.
By modifying version numbers,
the intruder can convince an SSL 3.0 client that it is communicating with a
2.0 server, and a 3.0 server that it is communicating with a
2.0 client. This will cause the parties to communicate using
SSL 2.0, giving the intruder an opportunity to exploit any of the known
weaknesses of SSL 2.0.
By modifying the parties' cryptographic preferences, the intruder can
force them into selecting a weaker encryption and/or signing algorithm
than they normally would. This may make it easier for the intruder to
decrypt the client's secret exchange message, or to forge the client's
signature.
The parties can prevent attacks on plaintext by repeating the exchange
of versions and cryptographic preferences once the handshake protocol is
complete;
the additional messages will be called verification messages.
Since the intruder cannot learn the shared secret, it cannot
compute the master secret and the derived keys and thus cannot interfere
with the parties' communication after they switch to the negotiated
cipher.
Suppose the intruder altered the cryptographic
preferences in the client's Hello message. When the client sends its
version and cryptosuite to the server under the just negotiated
encryption, the intruder cannot change them. The server will detect the
discrepancy and abort the protocol. This is also true for the server's
version and cryptosuite.
The above protocol is secure against attacks on version numbers
and cryptographic preferences except in the following
circumstances:
-
If an attack on version number in the first Hello
message causes the parties to switch to
a different protocol such as SSL 2.0, they will not exchange verification
messages and the attack will not be detected. See Section
4.9.2 for further discussion of anomalies related to the
version rollback attack. -
By changing cryptosuites in the Hello messages,
the intruder may force the parties to use a very weak
public-key encryption algorithm that can be broken in real time (i.e.,
while the current run of the handshake protocol is in progress). If the
intruder can break the encrypted message containing the client's secret,
it can compute the master secret and the derived keys and will thus be
able to forge post-handshake verification messages.
The only defense against this kind of attack
is to prohibit SSL implementations from using weak
cryptographic algorithms in the handshake protocol even if hello messages
from the protocol counterparty indicate preference for such
algorithms.
In Protocol D, the parties verify only plaintext information
after the handshake negotiation is complete. Since the intruder cannot
forge signatures, invert hash functions, or break encryption without the
correct private key, it can neither learn the client's secret, nor
substitute its own. It may appear that D provides complete
security for the communication channel between C and S. However,
Mur discovered an attack on client's identity that succeeds even if
all cryptographic algorithms are perfect.
Intruder I intercepts C's hello message to server S, and initiates
the handshake protocol with S under its own name. All messages
sent by S are re-transmitted to C, while most of C's messages,
including the post-handshake verification messages, are re-transmitted
to S. (See the protocol run below for details. Re-transmission of C's
verification message is required to change the sender identifier,
which is not shown explicitly below.)
As a result, both C and
S will complete the handshake protocol successfully, but C will be
convinced that it is talking to S, while S will be convinced that
it is talking to I.
Notice that I does not have access to the secret shared between C
and S. Therefore, it will not be able to generate or decrypt encrypted
messages after the protocol is complete, and will only be able to
re-transmit C's messages. However, the server will believe that the
messages are coming from I, whereas in fact they were sent by C.
This kind of attack, while somewhat unusual in that it explicitly
reveals the intruder's identity, may prove harmful for a number of
reasons. For example, it deprives C of the possibility to claim later
that it communicated with S, since S will not be able to support
C's claims (S may not even know about C's existence). If S is a
pay server providing some kind of online service in exchange for
anonymous ``electronic coins'' such as eCash [5], I may be
able to receive service from S using C's cash.
Recall, however, that
I can only receive the service if it is not encrypted,
which might be the case for large volumes of data.
To fix the bug in Protocol D, the parties verify all
of their communication after the handshake is complete. Now the intruder
may not re-transmit C's messages to S, because C's Hello message
contained C, while the Hello message received by the server contained
I. The discrepancy will be detected in post-handshake verification.
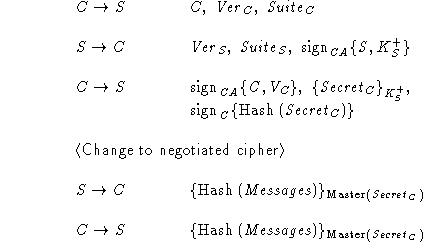
I observes a run of the protocol and records all of C's messages.
Some time later, I initiates a new run of the protocol, ostensibly
from C to S, and replays recorded C's messages in response to
messages from S. Even though I is unable to read the recorded
messages, it manages to convince S that the latter is talking to C,
even though C did not initiate the protocol.
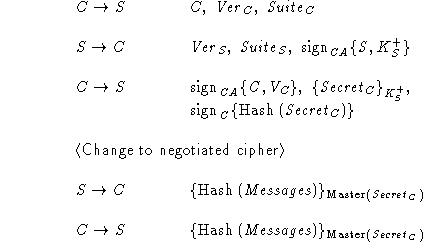
Next run of the protocol ...
By adding random nonces to each run of the protocol, SSL 3.0
ensures that
there are always some differences between independent runs of the protocol.
The intruder is thus unable to replay verification messages from one run in
another run.
The exact semantics of the verification messages exchanged after
switching to the negotiated cipher (i.e., Finished messages in
the SSL terminology) is somewhat unclear. Section 5.6.9 of [6]
states: ``No acknowledgment of the finished message is required;
parties may begin sending encrypted data immediately after sending the
finished message. Recipients of finished messages must verify that the
contents are correct.'' The straightforward implementation of this
definition led Mur to discover the following attack on Protocol
F:
- I modifies the Hello messages, changing the legitimate parties'
cryptosuites so as to force them into choosing a weak public-key encryption
algorithm for the secret exchange.
- I records the weakly encrypted
 as it is being
transmitted from C to S. - After C and S switch to the negotiated cipher, I delays
their verification messages indefinitely, preventing them from
discovering the attack on cryptosuites and gaining extra time to crack
the public-key encryption algorithm and learn .
- Once the secret is learned, I is able to compute the keys and
forge verification messages.
Since we did not model weak encryption that can be broken by the
intruder, we also did
not model the last step of the attack explicitly. Instead, if the model
reached the state after the third step, the attack was considered
successful.
Note that in the actual SSL 3.0 protocol
is not used directly as the symmetric key between C and S.
It serves as one of the inputs to a hash function that
computes the actual symmetric key. Therefore, even
if the intruder is able to figure out the symmetric key, this will not
necessarily compromise the shared secret .
To obtain , the intruder has to force
the parties into choosing weak public-key encryption
for the secret exchange message, and then
break the chosen encryption algorithm in real-time.
This attack can only succeed if both parties support
cryptosuites with very weak public-key encryption
(e.g., with a very short RSA key). We are not
aware of any existing SSL implementations
for which this is the case.
To prevent the attack on Protocol F, it is sufficient to require
that the parties consider the protocol incomplete until they each
receive the correct verification message. Mur did not
discover any bugs in the model implemented according to this semantics.
Alternatively, yet another piece of SSL can be added to Protocol
F. If the client sends the server a hash of all messages
before switching to the negotiated cipher, the server will be
able to detect an attack on its cryptosuite earlier.
Mur was used to model Protocol Z with 2 clients, 1 intruder, 1
server, no more than 2 simultaneous open sessions per server, and no
more than 1 resumption per session. No new bugs were discovered.
However, Mur found two anomalies in the protocol employed to resume
a session.
Adding the extra verification message suffices for the full handshake
protocol but not for the resumption protocol.
When a session is resumed, the
parties switch to the negotiated cipher immediately after exchanging
Hello messages. Therefore, the intruder can alter cryptographic
preferences in the Hello messages and then delay the parties'
Finished messages indefinitely, preventing them from detecting
the attack. It appears that this attack does not jeopardize the
security of SSL 3.0 in practice, since no secret is exchanged in the
resumption protocol. In fact, it is not clear to us if the cryptosuites in
the Hello messages are used at all in the resumption protocol.
In our model of Protocol Z,
the participants switch to SSL 2.0 if a
version number in the Hello messages is different from 3.0.
(Since the Internet draft for SSL 2.0 has expired and is not publicly
available at the moment, we included
a specification of SSL 2.0 in Appendix A.)
The Finished messages in SSL 2.0 do not include version numbers
or cryptosuites, therefore Protocol Z
is susceptible to the attack on cryptographic preferences
described in Section 4.5.
In the following example, it is assumed for simplicity that
client authentication is not used. Also, SSL 2.0 Hello messages
have a slightly different format than SSL 3.0 Hello messages and do
not contain explicit version information. To simplify presentation,
we assume that the intruder converts a 3.0 Hello message into
a 2.0 Hello message simply by changing the version number.
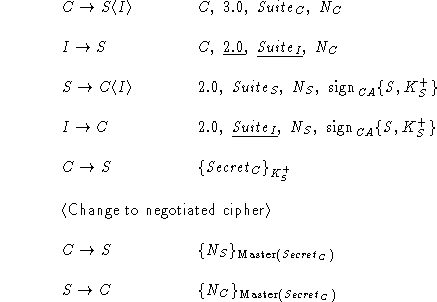
To prevent the version rollback attack, SSL 3.0 clients
add their version
number to the secret they send to the server. When
the server receives a secret with 3.0 embedded in it
from a 2.0 client, it can determine that there has been
an attack on the client's Hello message in which the client's
true version number (3.0) was rolled back to 2.0.
However, this defense does not work in the case
of session resumption.
Mur discovered a version rollback attack
on the resumption protocol. The attack succeeds since
in the resumption protocol, the client does not
send a secret to the server, and the intruder's alteration
of version numbers in the Hello messages goes undetected.
Strictly speaking, this attack is not a violation of the specification
[6], since the latter implicitly allows an SSL session
that was established using the 3.0 protocol to be resumed using
the 2.0 protocol. However, this attack makes implementations of
SSL 3.0 potentially vulnerable to SSL 2.0 weaknesses. Wagner
and Schneier [14] reach a similar conclusion in
their informal analysis of SSL 3.0.
Following is the
definition of the SSL 3.0 handshake protocol
according to [6]. When several messages from the same party
follow each other in the original definition, they have been
collapsed into a single protocol step (e.g., Certificate,
ClientKeyExchange, and CertificateVerify were joined into
ClientVerify). The underlined pieces of SSL 3.0 are not in
Protocol Z.
Assuming that the cryptographic functions are perfect, the
underlined pieces can be removed from the SSL 3.0 handshake protocol
without jeopardizing its security. However, they do serve a useful
purpose by strengthening cryptography and making brute-force attacks on
the protocol less feasible.
For example, recall that
the shared secret is not used directly as the symmetric
key between C and S. Instead, it is used as input to a
(pseudorandom) function that computes the actual shared secret.
Therefore, breaking the symmetric cipher will not necessarily compromise
the shared secret as it would require inverting two hash functions. To
obtain the shared secret, the intruder would have to break public-key
encryption in the ClientKeyExchange message.
The construction of the keyed hash in ClientVerify,
ServerFinished, and ClientFinished messages as
follows the HMAC method proposed by Krawczyk [7], who
proved that adding a secret key to the function makes it significantly
more secure even if the actual hash function is relatively weak.
In general, we would like to emphasize that SSL 3.0 contains many
security measures that are designed to protect the protocol against
cryptographic attacks. Since we modeled an idealized protocol in
Mur under the perfect cryptography assumption, we found SSL 3.0
secure even without these features.
While one goal of our analysis was ``rational reconstruction'' of
the SSL 3.0 handshake protocol, we were also interested in lessons to be
learned about using finite-state analysis to verify large protocols. We were
particularly concerned about the potentially very large number
of reachable
states, given that the SSL handshake protocol consists of 7 steps, and
each message sent in a particular
step includes several components, each of which
can be changed by the intruder under certain conditions.
Our model of the intruder is very simple and straightforward. There is
no intrinsic knowledge of the protocol embedded in the intruder, nor
does the design of the intruder involve any prior knowledge of any form
of attack. The intruder may monitor communication between the protocol
participants, intercept and generate messages, split intercepted
messages into components and recombine them in arbitrary order. No
clues are given, however, as to which of these techniques should be used
at any given moment. Therefore, the effort involved in implementing the
model of the intruder is mostly mechanical.
The following simple techniques proved useful in reducing the number of
states to be explored:
- Full knowledge.
-
We assume that every message sent on the network is intercepted by the
intruder. Clearly, this assumption does not weaken the intruder.
Without it, however, most of the states that Mur
explored were identical as far as the state of the legitimate
participants was concerned and the only difference was the contents of the
intruder's database. By ensuring that the database is always as full as
it can possibly be (i.e., it includes all knowledge that can be
extracted from the messages transmitted on the network thus far), we
achieved an order of magnitude reduction in the number of reachable states
(e.g., from approximately 200,000 to 5,000 for a single run of the
protocol).
- No useless messages.
-
We optimized our intruder model to only
generate messages that are expected by the legitimate
parties and that
can be meaningfully interpreted by them in their current
state. Since at any point in the protocol sequence, each party is
expecting only one particular type of message,
the number of message types the intruder
generates at each step does not exceed the number of protocol
participants. Still, the number of ways in which the intruder could
construct individual messages might be large since messages are
generated from the message
components (keys, nonces, etc.) stored in the intruder's database.
- No useless components.
-
If the intercepted message can be completely recreated from
the components already in the intruder's database, the message is
discarded.
- Flags.
-
Every procedure executed by the protocol participants after receiving a
message is guarded by a flag. By changing flag values, we can turn on
and off pieces of the protocol, enabling incremental and ``what-if''
modeling (e.g., what happens if the server does not verify the hashed
secret it receives from the client).
Running under Linux on a Pentium-120 with 32MB of RAM, the verifier
requires
approximately 1.5 minutes to check for the case of 1 client, 1 server, 1
open session, and no resumptions. Less than 5000 states are explored.
The largest instance of our model that we verified
included 2 clients, 1 server, no
more than 2 simultaneous open sessions per server, and no more than 1
resumption per session. Checking took slightly under 8 hours, with
193,000 states explored.
Our study shows that the finite-state enumeration tool
Mur can be successfully applied to
complex security protocols like SSL. The analysis uncovered
some anomalies in SSL 3.0. (None of these anomalies, however,
poses a direct threat to the security of SSL 3.0.)
Of these anomalies at least one
had slipped through expert human analysis, confirming the
usefulness of computer assistance in protocol design.
We are seeking to improve on the current limitations of our
approach in three ways. First, modeling a complex
cryptographic protocol in the Mur language is a relatively
time-consuming (but straightforward) task. Automatic translation
from a high-level protocol description language like CAPSL
to Mur could significantly reduce the
human effort for the analysis.
Second, often the protocols have very large numbers of reachable
states. Thus, we plan to develop techniques
that reduce the number of states that have to be explored when
analyzing cryptographic protocols.
Finally, ``low level'' properties of the cryptographic functions
used in a protocol often cause the protocol to fail, even if it
appears to be correct at the high level. We plan to extend
our modeling approach to allow detection of such protocol
failures by developing more detailed protocol models.
We are grateful to the members of our research group for
discussions of the SSL protocol, which resulted in a better
understanding thereof. We would also like to thank the
anonymous reviewers for comments that helped to
clarify further details of the SSL protocol.
This appendix outlines the SSL 2.0 protocol. In the protocol
description
below,  is a number that identifies a particular session.
When the server starts a new session with the client, it assigns
it a fresh . When the client wants to resume a previous session,
it includes its in the Hello message, and the server
returns  which is the same session number
with the ``session found'' bit set.
Notice that the basic SSL 2.0 protocol shown above does not protect plaintext
transmitted in the Hello messages, making the protocol
vulnerable to version rollback and cryptographic preferences
attacks described in Section 4.5 above.
A description of other weaknesses in SSL 2.0
can be found in SSL-Talk FAQ [1].
In the SSL 2.0 resumption protocol with authentication shown below,
 is the means of authentication desired
by the server,  is the server's challenge, 
is the type of the certificate provided by the client,
 is the actual certificate (e.g., a CA-signed certificate
for the client's verification key), and
 is the data that authenticates the client
(e.g., signed challenge  ).
The SSL 3.0 master secret is computed using
where  . In most of this paper,
the master secret is denoted simply as  .
References
- 1
-
Consensus Development Corporation.
Secure Sockets Layer discussion list FAQ,
https://www.consensus.com/security/ssl-talkfaq.html, September 3, 1997.
- 2
-
S. Dietrich.
A Formal Analysis of the Secure Sockets Layer Protocol.
PhD thesis, Dept. Mathematics and Computer Science, Adelphi
University, April 1997.
- 3
-
D. L. Dill.
The verification system.
In Computer Aided Verification. 8th International Conference,
pages 390-3, 1996.
- 4
-
D. L. Dill, S. Park, and A. G. Nowatzyk.
Formal specification of abstract memory models.
In Symposium on Research on Integrated Systems, pages 38-52,
1993.
- 5
-
https://www.digicash.com/ecash/ecash-home.html.
- 6
-
A. O. Freier, P. Karlton, and P. C. Kocher.
The SSL protocol version 3.0.
draft-ietf-tls-ssl-version3-00.txt, November 18, 1996.
- 7
-
H. Krawczyk, M. Bellare, and R. Canetti.
HMAC: Keyed-hashing for message authentication.
Internet Request For Comments RFC-2104, February 1997.
- 8
-
G. Lowe.
Breaking and fixing the Needham-Schroeder public-key protocol
using CSP and FDR.
In 2nd International Workshop on Tools and Algorithms for the
Construction and Analysis of Systems. Springer-Verlag, 1996.
- 9
-
J. C. Mitchell, M. Mitchell, and U. Stern.
Automated analysis of cryptographic protocols using Mur .
In IEEE Symposium on Security and Privacy, pages 141-51, 1997.
- 10
-
https://verify.stanford.edu/dill/murphi.html.
- 11
-
S. Schneider.
Security properties and CSP.
In IEEE Symp. Security and Privacy, 1996.
- 12
-
U. Stern and D. L. Dill.
Automatic verification of the SCI cache coherence protocol.
In Advanced Research Working Conference on Correct Hardware
Design and Verification Methods, pages 21-34, 1995.
- 13
-
D. Wagner.
Email communication, August 23, 1997.
- 14
-
D. Wagner and B. Schneier.
Analysis of the SSL 3.0 protocol.
In 2nd USENIX Workshop on Electronic Commerce, 1996.
Revised version of November 19, 1996 available from
https://www.cs.berkeley.edu/~daw/ssl3.0.ps.
- 15
-
L. Yang, D. Gao, J. Mostoufi, R. Joshi, and P. Loewenstein.
System design methodology of UltraSPARC
 -I.
In 32nd Design Automation Conference, pages 7-12, 1995.
- ...SSL 3.0
-
This work was supported in part by the
Defense Advanced Research Projects Agency through NASA
contract NAG-2-891,
Office of Naval Research grant N00014-97-1-0505,
Multidisciplinary University Research Initiative
"Semantic Consistency in Information Exchange",
National Science Foundation grant CCR-9629754, and the Hertz Foundation.
The views and conclusions contained in this document are those
of the author(s) and should not be interpreted as representing the
official
policies, either expressed or implied, of the
Defense Advanced Research Projects Agency, NASA, ONR, NSF or the US
Government.
Finite-State Analysis of SSL 3.0
This document was generated in part using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
|
the number that S considers the shared secret.
Then 
)
only if S is already in the state
in which it is ready to start communicating with C using
the negotiated cipher
( 
).
Conversely, S should reach the state
Technical Program