Praveen Yalagandula
,
Suman Nath
,
Haifeng Yu
,
Phillip B. Gibbons
,
Srinivasan Seshan
The University of Texas at Austin Carnegie
Mellon University Intel Research Pittsburgh
A key challenge in designing large, long running distributed systems is to mask the failures that arise among the system components. This challenge becomes more acute as the number of machines and the population of users increase, i.e., precisely when the system becomes more useful. In order to design systems resilient to the machine failure characteristics in real deployments, it is necessary to study these characteristics and develop design principles tailored to them.
In this paper, we analyze traces [1,2,12] from three large distributed systems (PlanetLab, Domain Name System (DNS), and a collection of over 100 web servers) in order to characterize machine failures in these systems. Although many previous research efforts [2,3,5,6,13] have also investigated machine failure characteristics, our study focuses on important properties beyond these initial findings, and suggests how these properties may strongly influence the design of large distributed systems. In particular, we start by addressing the following important--but perhaps subtle--questions not answered by previous studies:
The answers to these questions can significantly influence the design of large distributed systems targeting high system availability. For example, both Total Recall [4] and CFS [7] determine the degree of replication assuming failure independence. If the correlation level is high, such designs need to be revisited. As another example, consider End System Multicast (ESM) [9], an overlay multicast system that utilizes well-provisioned infrastructure nodes (called waypoints) to construct better multicast trees. The failure of a waypoint will cause temporary interruption of the service followed by the repair of the multicast tree with new waypoints. Clearly, the system availability of ESM is affected by the MTTF rather than the availability of the machines selected as waypoints. On the other hand, there are other systems (see Section 3) that care more about the MTTR of its machines. If high availability of a machine does not always imply good MTTF (or MTTR), then a system should not simply favor the use of machines with high availability.
Based on the findings from our study of the aforementioned questions, we derive four fundamental design principles for highly available distributed systems:
Our study is based on traces from three large distributed systems: PlanetLab, DNS, and a collection of over 100 web servers. We call the three traces PL_trace, DNS_trace, and WS_trace respectively. The DNS and web server traces are intended to be representative of public-access machines that are maintained by different administrative domains, while the PL_trace potentially describes the behavior of a centrally administered distributed system that is used mainly for research purposes. There are also many other failure traces available, such as for P2P systems [3,13] and for campus-wide networks [5]. In this paper, we intentionally focus on machine failure characteristics in non-P2P wide-area distributed systems.
All three traces are probe traces rather than node up/down logs. The nature of these probe traces requires us to carefully address the effects of network failures that demonstrate themselves as node failures. Also, we are unable to detect short-duration failures or recoveries between probes. On the other hand, using probe traces enable us to study public/commercial systems that typically do not publish up/down logs.
PL_trace [1] contains probes between all pairs of nodes (277 on average) in PlanetLab from March 2003 to June 2004. Each probe consists of 10 pings, and we say that a probe fails if and only if all 10 pings fail. We refer to a complete cycle of all pair-probes as a probe interval, which is around 15 to 20 minutes in PL_trace. We consider a node to be unavailable or down during a particular probe interval if and only if none of the nodes from other domains can ping it. We consider two nodes to be in the same domain if they share the first 24 bits of their 32-bit IP addresses. In this study, we do not distinguish between whether a node has failed or has simply been partitioned from all other nodes not in the local domain--in either case it is unavailable to the system. A node is available or up if it is not down. Other more stringent definitions of availability could be used instead. For example, we could consider a node to be available only if it can be pinged from a threshold fraction of other nodes. See [15] for discussions on these other possible definitions.
WS_trace [2] contains logs of HTTP GET requests from a single source node at CMU to 130 Web servers from
September to December 2001. As in PL_trace, we call a complete cycle of all
HTTP requests a probe interval, which is around 10 minutes in
WS_trace. In this trace,
near-source network partitions make it appear as if all the web
servers have failed. To mitigate this effect, we use the following
simple filtering. If four or more consecutive HTTP requests to different
servers fail, we assume that the probing node has become disconnected
from the Internet and thus ignore all those consecutive failures. All
other failed probes are considered web server failures. We choose four
as the threshold because if we used a lower threshold, we
would view the client (on Internet2) as experiencing near-source
failures around 
% of the time, which is rather unlikely. Note that
this heuristic may still not perfectly classify source and server
failures, but the error is likely to be well controlled.
DNS_trace [12] contains probes from a single machine to over 231,000 DNS servers for two weeks. Each server was probed at an exponentially distributed period with a mean of 1 hour. Near-source failures have already been addressed [12] in this trace, thus filtering (as used for WS_trace) is not needed and all failed probes are treated as DNS server failures. Our study analyzes a subset of around 25,000 servers that had at least one failure during the measurement period.
We measure Time-to-Failure (TTF) and Time-to-Repair (TTR) of a node as
the contiguous time periods for which that node is available and
unavailable respectively. The availability of a node is the
fraction of time for which the node is available. We report
availability in terms of its number of nines (i.e.,
where 
is the availability).
Intuitively, a highly available machine should also have good MTTF and good MTTR. The reason is that a highly available machine is generally well maintained, and hence should not fail very often and should recover more quickly. Under this assumption, it suffices to consider only node availability, rather than MTTF and MTTR separately. But is this intuition correct?
Figure 1 plots the relationship of availability to MTTF and MTTR in PL_trace. The results for WS_trace and DNS_trace are similar [15]. Even though there is a general trend toward better MTTR and MTTF (especially for MTTR) when availability increases, notice that the range on MTTF and MTTR is large for any given availability value. This means that if we need to choose between two machines, picking the one with better availability does not always give us the one with better MTTF or MTTR. Indeed, our analysis shows that among 30% (20%) of all possible pairs of machines in PL_trace, the one with higher availability does not have higher MTTF (lower MTTR, respectively). For WS_trace, the numbers are 15% and 26%, respectively, and for DNS_trace, they are 28% and 20%, respectively. Note that even when choosing one node randomly out of a pair of nodes, the probability of choosing the wrong node is just 50%.
Figure 2 plots the MTTR and MTTF of individual
machines in the three traces. Since DNS_trace has a large number of
nodes, to improve clarity, we only plot 250 randomly chosen (out of around 25,000) nodes in the graph.
If good availability is synonymous with good MTTF and good MTTR, it
necessarily means that good MTTF implies good MTTR as well. Under such an
assumption, the points in Figure 2 should roughly
form a monotonically decreasing trail. This is clearly not what we see in
Figure 2.
Furthermore, the correlation coefficient 
is very small in all three
traces (
for PL_trace, 
for WS_trace, and
for DNS_trace), implying little correlation between the MTTR and MTTF of
a machine.
Design principle P1. Good availability of a machine does not always imply good MTTR and good MTTF. Given that different systems may care more about either MTTF or MTTR (see Section 3), a system should monitor MTTF and MTTR (instead of only availability) separately when choosing which machines to use.
|
 |
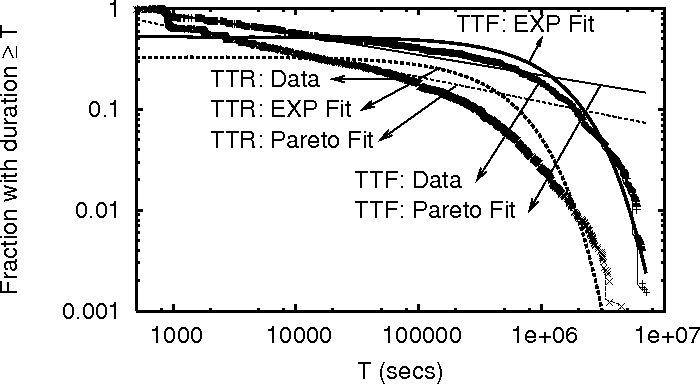
It is well known that the lifetime of Unix processes follows a Pareto
distribution [8] (i.e., a process that has been running
for time 
will continue to run for time with constant
probability), and this property has been used in dynamic load
balancing [8]. Is it possible to similarly predict how
long a machine will remain up given how long it has been up?
We analyze the TTF and TTR of all machines in PL_trace in a similar
way as in [8]. We plot the TTF and TTR distributions in
Figure 3 along with best fitting exponential
(
) and Pareto (
) distributions. An
exponential distribution is entirely memoryless, meaning that no
information can be extracted based on how long the machine has been up
or down. Figure 3 shows that neither distribution
fits the data perfectly, but the exponential distribution fit is
better.
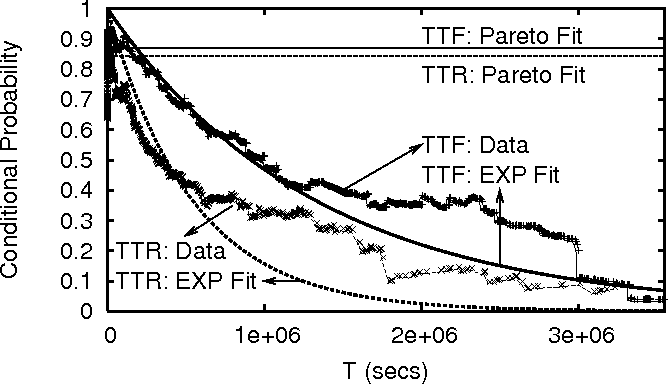
To gain additional understanding, we compute the following
conditional probability: Prob[a node continues to be available (or
unavailable) for time 
it has been available (or unavailable) for
time ]. For exponential and Pareto distributions, this conditional
probability is
and 
respectively. Figure 4 plots this conditional
probability computed from PL_trace, along with the
probabilities computed for exponential and Pareto fits. Clearly the
conditional probability from the trace follows the exponential distribution
more closely. We observe similar behavior [15]
for TTF in WS_trace; the
TTR in WS_trace is close to neither the exponential nor the Pareto
distribution. In DNS_trace, the time period between two consecutive
probes to the same DNS server follows an exponential
distribution with a mean of 1 hour. This relatively large period
between probes (as compared to around 15 minutes in PL_trace and
WS_trace) can cause inaccuracies in individual TTR
and TTF values, and, thus, we do not perform the above analysis for DNS_trace.
Overall, our analysis shows that the TTF and TTR of a node
are hard to predict based on how long the node has been up or down.
Although we cannot predict how long a machine will remain up given how long it has been up, is it possible to predict TTF (or TTR) from MTTF (or MTTR)? Specifically, if the variation in TTF (or TTR) were small, we could indeed predict TTF (or TTR) based on the historical MTTF (or MTTR). Figure 5 plots the coefficient of variance (defined as the ratio of standard deviation to mean) of TTR and TTF in PL_trace. Most nodes have a coefficient greater than 1.0 which implies quite a wide probability distribution. Similar results [15] hold for WS_trace. Again, we do not analyze DNS_trace for previously mentioned reasons.
 |
Given that TTR and TTF cannot be accurately predicted, we turn to the predictability of MTTF and MTTR. We split the traces into two parts and for each node compare the MTTR and MTTF observed in one part with the other. Figure 6 plots the percentage difference in MTTR and MTTF between the first 8 months and the remaining 9 months of PL_trace. Clearly, the MTTR and MTTF for most nodes do not vary significantly over the two periods. We also observe similar results [15] for WS_trace. We do not perform this study for DNS_trace because of its short duration.
Design principle P2. Given the predictability of MTTF and MTTR, a system should monitor machine MTTF and MTTR and use this knowledge to achieve better availability.
Design principle P3. Given that TTF and TTR cannot be predicted with reasonable accuracy based on current uptime, downtime, MTTF, or MTTR, a system should not rely on such prediction.
Here we investigate how strong failure correlation is for PlanetLab nodes and for the collection of web servers. Since correlated failures tend to be rare, we need a long trace to observe them; so, we do not study DNS_trace because of its short duration. We are interested in the distribution for the number of near-simultaneous failures. In each probe interval, we determine the number of near-simultaneous failures by counting the number of nodes that are unavailable in the interval but were available in the previous interval.
Figures 7 and 8 plot the PDF for
the number of near-simultaneous failures
in PL_trace and WS_trace, respectively. We observe that
large-scale correlated failures do happen: PL_trace shows an
event where 58 nodes failed near-simultaneously; while
WS_trace has a failure event of 42 web servers.
Both graphs also show the fitting of the beta-binomial distribution
(BBD) and geometric
distribution to the measured data. BBD is used in [11] to
model correlated failures in different software versions, and also
by Bakkaloglu et al. [2] to model
correlation in WS_trace. The geometric distribution is a simple
distribution where the probability of having 
simultaneous failures
is 
, where 
is a constant and 
is the
normalization factor. Neither model seems to be a good fit for our
data, especially for large-scale correlated failures. Finding a better
fitting analytical model is beyond the scope of this paper.
Design principle P4. The level of correlation among machine failures is not trivial. Designs for high availability should explicitly take correlation into account.
Overlay Multicast (Principles applied: P1, P2). As mentioned in Section 1, ESM [9] should focus on the MTTF of the waypoints - just favoring waypoints with good availability will result in a suboptimal design.
Distributed Storage Systems (Principles applied: P1, P2). Almost all distributed storage systems (e.g., CFS [7]) use replication to ensure data availability. They also incorporate repair mechanisms (called regeneration) to create new replicas when existing replicas fail. Such replica creation typically takes a certain time
, depending
on the amount of data to be transferred.
If all the live replicas fail within this window of
, the system becomes unavailable and has to wait for at least
one replica to recover. We define system availability as the
fraction of time that at least one replica is available.
Now let us consider a set of replicas with the same MTTF, MTTR and
availability. A simple analysis will show that system availability
is determined by the ratios among , MTTF and MTTR.
Specifically, the effect of doubling both MTTF and MTTR (and hence
keeping the replica availability unchanged) on system availability
is the same as halving . Smaller , in turn, yields better
system availability. Thus, system availability is not uniquely
determined by replica availability, rather it increases with
replica MTTF and MTTR even though replica availability remains the
same. As a result, when determining the number of replicas needed
to achieve a target system availability, considering only the
availability of individual replicas is not sufficient.
An Oracle for Repair (Principle applied: P3). In the evaluation of Total Recall [4], Bhagwan et al. use an Oracle with exact knowledge about when failures will occur. This Oracle repairs an object just before the last remaining replica fails. Their results show that the Oracle is about an order of magnitude better than the actual design in Total Recall. A natural question to ask is whether we can approximate the Oracle by predicting failures based on history. Our findings show that we are unlikely to be able to accurately predict individual failure events, and a design along these lines is unlikely to be effective.
Regeneration Systems with Strong Consistency (Principles applied: P1, P2). Regeneration systems (systems that repair failed replicas by creating new ones) supporting strong data consistency, such as RAMBO [10] and Om [17], need to ensure that regeneration is performed in a consistent fashion. Otherwise if multiple replicas regenerate simultaneously, the system may end up with multiple disjoint replica groups. To avoid this problem, such systems typically use majority voting for mutual exclusion. To achieve better fault tolerance, such voting can be done on nodes outside the replica group [17].
In this case study, we focus on the nodes forming the voting system for
regeneration. We say that the voting system is down if we lose a
majority, otherwise it is up. Thus, this voting system also has
its own MTTF and MTTR, which increases monotonically with node MTTF
and MTTR. We will show that even when the availability of the
voting system is kept constant, a smaller MTTR will yield better
system availability for the replica group. This can be best explained
using Figure 9. Regeneration starts whenever a replica
fails and must complete before all remaining replicas fail, otherwise
the overall system becomes unavailable. This provides a window 
of
opportunity to regenerate.
Because of this window, we can
mask considerable durations of unavailability of the voting system.
If the downtime of the voting system is always smaller
than this window (as in system (b) in Figure 9),
then the overall system is always available. This means that we should
favor nodes with small MTTR in constructing the voting system.
 |
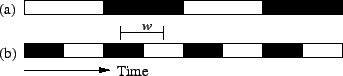Majority Voting Systems (Principle applied: P4). Correlation in failures can significantly affect the behavior of traditional fault-tolerant designs such as majority voting [14]. Figure 10 shows the unavailability of a simulated majority voting system with nodes having the MTTF(
days) and MTTR(
days) that we found for PlanetLab machines.
We model the correlated failures using the geometric distribution
mentioned in Section 2.4 with 
. As the
graph shows, majority voting is significantly worse under correlated
failures. In real systems where we observe higher correlation
than modeled by the geometric distribution, we expect further
decay in availability.
This
implies that correlation in today's real systems has reached such
a level that it has to be considered explicitly in system design.
For example, signed quorum systems [16] may
potentially be used in place of majority voting to provide better
protection against correlated failures.
In this paper, we extend the state-of-the-art in understanding machine availability by investigating machine failure characteristics using traces from three large distributed systems. Based on our findings (many of which are perhaps counter-intuitive), we derive a number of fundamental principles for designing highly available distributed systems. We further show with several case studies that our design principles can significantly influence the availability design choices in real systems.
strib/pl_app/.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons main-html
The translation was initiated by Praveen Yalagandula on 2004-11-04
TTF (or TTR) 
] computed from PL_trace,
together with the probability calculated from the exponential and
Pareto fits in Figure 
