The most conclusive validation of the metric presented in this paper would be to collect data from actual development projects. Since the VC metric presented in this paper is intended to give an estimate of the effort required to test a class, a possible experiment would be to apply the metric to a set of classes, predict the amount of effort required to test each one and then to have each class tested by a developer. The actual effort required to test each could be obtained and the accuracy of the prediction could be measured.
Since such experiments are difficult to control and even more difficult to have approved, we propose an alternative approach in which the number of test cases required to achieve a specified level of test coverage is used to estimate the total testing effort. For our experiment we used branch coverage[2] as our coverage criteria. The criteria chosen is irrelevant provided that it is recognized as a valid, and likely, technique that might be used by developers on an actual project.
One criteria for the level of test coverage that is important is that the testing technique should utilize the same level of information as VC. The value of VC presented here is the internal visibility because it considers attributes that are not visible external to the object. This estimate would approximate the amount of effort that would be devoted to testing the individual methods. This internal view corresponds more closely to a structural testing approach, such as branch testing, than to a specification-based approach. In the conclusion section we will consider the external visibility of an object that corresponds to specification-based testing.
For our experiment, we chose classes from several sources including locally written code and widely used libraries. The VC was calculated for each method and each class. Each modifier method was examined and the number of branch test cases needed to achieve 100% branch coverage of each method was calculated.
A non-parametric correlation statistic, Spearman's rho, was used to determine the amount of agreement between the number of test cases required to give 100% branch coverage and the internal visibility. This comparison resulted in a correlation of .35. The significance of the correlation was investigated using the student's t distribution due to the sample size. The correlation was found to be significant at the .1 confidence level.
Initial comparisons were less successful than the present one because they included both accessor and modifier methods. Accessor methods confound the VC metric in that there is more information flowing out than flowing in. Accessor methods are also very simple structurally and usually have only one path; therefore, the testing effort is negligible. For this experiment and those reported below, accessor methods were excluded from the calculation.
Several other experiments have been conducted to experimentally validate the metric.
The testability of a method is directly related to the complexity of its structure[14]. Using the original set of classes, we computed the cyclomatic complexity for each method. Once again there was statistically significant agreement between VC and the cyclomatic complexity.
: Example Solutions to a Design Problem
: Example Calculations for VC
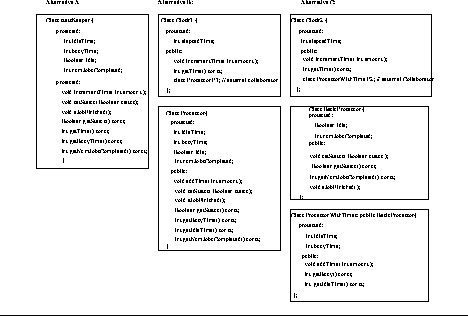
In a previous study[1], a set of design problems was presented to a group of developers experienced in object-oriented design. Figure 2 presents one set of design solutions for a problem in tracking the idle time for a set of processors. The developers were asked to rank three solutions to each design problem. These rankings were then compared to the rankings computed using a complexity metric, Permitted Interactions. In a subsequent study another metric, intended for use even earlier in the development process, was compared to these expert rankings. In each case, statistically significant agreement was found.
: Preferences by experts, PC,PI and VC
For the testability metric, a similar comparison was made between the
rankings by experts and the VC metric. Figure 3 shows the
visibility calculations for the design alternatives. The results of the
comparison are shown in
table 
. The VC metric agreed with the expert rankings
in 14 of the 17 cases. In two of the three cases for which there was
disagreement, previous studies[1,12] had also shown some disagreement indicating
that these examples may have alternatives that are too closely related.
