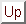
We describe the main design considerations for QML in Section 4.1. We already introduced the fundamental concepts of QML in section 1. Sections 4.2--4.8 describe the syntax and semantics of QML in more detail. For the full description of QML we refer to the language definition in [].
The main design consideration for QML is to support QoS specification in an object-oriented context. We want QML to integrate seamlessly with existing object-oriented concepts. This overall goal results in the following specific design requirements for QML:
Other aspects such as negotiation and utility can be dealt with as mechanisms using QML or possibly be part of future extensions of QML. This paper focuses on the requirements listed above.
We have already briefly introduced the fundamental concepts of QML: contract type , contract , profile . The following sections will provide a more detailed description of QML.
A contract type contains a dimension type for each of its dimensions. We use three different dimension types: set, enumeration, and numeric. Figure 5 gives an abstract syntax for contract and dimension types.
Figure: Abstract syntax for contract types
Contracts are instances of contract types. A contract type defines the structure of its instances. In general, a contract contains a list of constraints. Each constraint is associated with a dimension. For example, if we have a dimension ``latency'' in a contract type, a contract instance may contain the constraint ``latency < 10.'' Figure 6 gives an abstract syntax for contracts and constraints.
A contract may specify constraints for all or a subset of the dimensions in its contract type. Omission of a specification for a particular dimension indicates that the contract is trivially satisfied along that dimension.
Figure: Abstract syntax for contracts
In general, a constraint consists of a name, an operator, and a value. The name is typically the name of a dimension, but, as we describe in Section 4.3, the name can also be the name of a dimension aspect. The permissible operators and values depend on the dimension type. A dimension type specifies a domain of values. These values can be used in constraints for that dimension. The domain may be ordered. For example, a numeric domain comes with a built-in ordering (``<'') that corresponds to the usual ordering on numbers. Set and enumeration domains do not come with a built-in ordering; for those types of domains we have to describe a user-defined ordering of the domain elements. The domain ordering determines which operators can be used in constraints for that domain. For example, we cannot use inequality operators (``<,'' ``>,'' ``<=,'' ``>='') in conjunction with an unordered domain.
The domain for a set dimension contains elements that are sets of
name literals. We specify a set domain using the keyword 
,
as in ``
.'' This defines a
set domain where the domain elements are subsets of the set
``
.'' The constraints over a set
dimension will then be constraints with set values, as in
``
.''
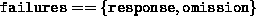The domain for an enumeration dimension contains elements that are
name literals. We specify an enumeration domain using the keyword
. For example, we could define an enumeration domain as
follows: ``
.'' Here, the
domain will contain the name literals ``
,''
and we can specify constraints as ``
.''
The domain of a numeric dimension contains elements that are real
numbers. Constraints for a numeric dimension are written as
``
.''
Elements of numeric dimensions are always ordered. We can specify a
user-defined ordering for set and enumerated dimensions in the
following way: ``
.''
When dimensions are ordered we need to specify whether larger or smaller
values are considered stronger. As an example consider the dimension
of availability. A larger numeric value for availability is a stronger
that a smaller, we say that availability is an ``increasing'' dimension.
Other dimensions, such as delay, are ``decreasing'' since smaller values are
consider as stronger guarantees. Consequently, QML requires that we
define ordered dimensions as either decreasing or increasing. For
the data validity enum decreasing semantics seems most intuitive, since
valid
also satisfies invalid
.
The example in Figure 7 gives an example of a contract type expression followed by a contract expression. Note that the contract expression is explicitly typed with a contract type name, this explicit typing enables the QML compiler to determine a unique contract type for any contract expression. So far we have only covered the syntax for contract values and contract types. In Section 4.4, we describe how to name contract values and contract types, and how to use those names in contract expressions.
Figure: Example contract type and contract expressions
In addition to simple constraints QML supports more complex characterizations that are called aspects . An aspect is a statistical characterization; QML currently includes four generally applicable aspects: percentile , mean , variance , and frequency . Aspects are used for characterizations of measured values over some time period.
The percentile aspect defines an upper or lower value
for a percentile of the measured entities. The statement
denotes the strongest P percent of the
measurements or occurrences that have been observed.
The aspect ``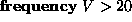
'' states that
the 80 th percentile of measurements for the dimensions
must be less than 6. We allow a constraint for a dimension to
contain more than
one percentile aspect, as long as the same percentile P does not
occur more than once.
QML also allows the specification of frequency constraints for individual
values which is useful with enumerated types, and for ranges, which is
useful with numeric dimensions. Rather than specifying
specific numbers for the frequency, QML allows us to specify the relative
percentage with which values in a certain range occur.
The constraint ``
%''
means that in more that 20% of the occurrences we should have the
value V. The literal V can be a single value or if the dimension
has an ordering, and only then, it may be a range. The constraint
``
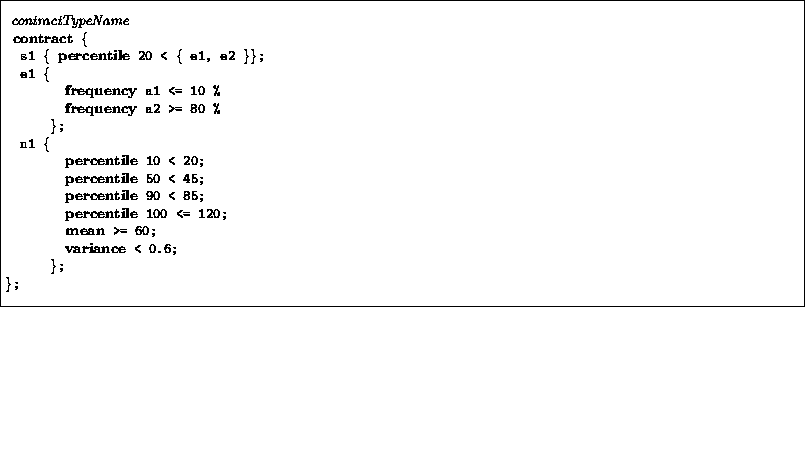%'' means that we
expect 35% of the actual occurrences to be larger than 1 and less than
or equal to 3.
Figure 8 shows some examples of aspects in contract expressions. The contract expression is preceded by the name of its corresponding contract type. For s1 we define one constraint for the 20th percentile. The meaning of this is that the strongest 20% of the value must be less than the specified set value.
For e1 we define the frequencies that we expect for various values. For the value a1 we expect a frequency of less than or equal to 10%. For a2 we expect a frequency greater than or equal to 80%, and so forth.
The constraint on n1 defines bounds for values in different percentiles over the measurements of n1 . In addition, we define an upper bound for the mean and the variance.
Figure: Example contract expression
The definition of a contract type binds a name to a contract type;
the definition of a contract binds a name to the value of a contract
expression. Figure 9 illustrates the abstract syntax
to define contracts and contract types. In the astract syntax, we use
as a generic name for contracts and y as a generic name for
contract types.
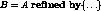
Figure: Abstract syntax for definition of contracts and
contract types
We can define a contract B to be a refinement of another contract A
using the construct ``
''
where A is the name of a previously defined contract. The contract that
is enclosed by curly brackets (
) is a ``delta'' that
describes the difference between the contracts A and B. We say that
the delta refines
A and that B is a refinement
of A.
The delta can specify QoS properties along dimensions for which
specification was omitted in A. Furthermore, the delta can replace
specifications in A with stronger specifications. The notion of
``stronger than'' is given by a conformance relation on constraints.
We describe conformance in more detail in
Section 4.8.
Figure 10 and Figure 11 illustrates how a named contract type ( Reliability ) can be define and how contracts of that type can be defined respectively. The contract type Reliability has the dimensions that we have identified within the QoS category of reliability described in section 3
Figure: Example contract type definition
Figure: Example contract definitions
The contract systemReliability is an instance of Reliability ; it captures a system wide property, namely that operation invocation has ``exactly once'' (or transactional) semantics. The systemReliability only provides a guarantee about the invocation semantics, and does not provide any guarantees for the other dimensions specified in the Reliability
contract type.
The contract nameServerReliability is defined as a refinement of another contract, namely the contract bound to the name systemReliability . In the example, we strengthen the systemReliability contract by providing a specification along the serverFailure dimension, which was left unspecified in the systemReliability contract.
According to our definition, a service specification contains an interface and a QoS profile. The interface describes the operations and attributes exported by a service; the profile describes the QoS properties of the service. A profile is defined relative to a specific interface, and it specifies QoS contracts for the attributes and operations described in the interface. We can define multiple profiles for the same interface, which is necessary since the same interface can for example have multiple implementations with different QoS properties.
Once defined, a profile can be used in two contexts: to specify client QoS requirements and to specify service QoS provisioning. Both contexts involve a binding between a profile and some other entity. In the client context this other entity is the service reference used by the client; in the service context, the entity is a service implementation. We discuss bindings in Section 4.7. Here, we describe a syntax for profile values, and in Section 4.6 we describe a syntax for profile definition.
Figure: Abstract syntax for profiles
Figure 12 gives an abstract syntax for profiles. A profile is a list of requirements, where a requirement specifies one or more contracts for one or more interface entities, such as operations, attributes, or operation parameters. If a requirement is stated without an associated entity, the requirement is a default requirement that applies by default to all entities within the interface in question. Our intention is that the default contract is the strongest contract that applies to all entities within an interface. We can then explicitly specify a stronger contract for individual entities by using the refinement mechanism.
Contracts for individual entities are defined as follows:
``
.'' Here e is an entity and
C is a contract. We use C as a delta that refines the default
contract of the enclosing profile. Using individual entity contracts
as deltas for refinement means that we do not have to repeat the
default QoS constraints as part of each individual contract.
Although a profile refers to specific operations and arguments within an interface, the final association between the profile and the interface is established in a profile definition. Such definitions are described in section 4.6.
For each contract type, such as reliability, that a profile involves, we may specify zero or one default contract. In addition, at most one contract of a given type can be explicitly associated with an interface entity.
If, for a given contract type T, there is no default contract and there is no explicit specification for a particular interface entity, the semantics is that no QoS properties within the category of T are associated with that entity.
Figure: Abstract syntax for definition of profiles
A profile definition associates a profile with an interface and gives
the profile a name.
A general requirement is that the interface entities referred to
by the profile must exist in the related interface.
The syntax for profile definition is given in
Figure 13 . The definition ``
'' gives the name 
to the
profile which is the result of evaluating the profile expression
with respect to the interface 
.
The profile name can be used to associate this particular profile
with implementations of the intName
interface or with references
to objects of type intName
.
A profile expression ( profileExp
) can be a profile, or an
identifier with a ``
'' clause. If the expression is a
profile value, the definition binds a name to this value. If a
profile expression contains an identifier and a ``
''
clause, the identifier must be the name of a profile, and the
``
'' clause then refines this profile. The definition
gives a name to this refined profile.
If we have a profile expression ``
,'' then the delta must either add to the specifications
in A or make the specifications in A stronger. The delta can add
specifications by defining individual contracts for entities that do
not have individual contracts in A. Moreover, the delta can specify
a default contract if no default contract is specified in A. The
delta can strengthen A's specifications by giving individual contracts
for entities that also have an individual contract in A. The
individual contract in the delta are then used as a contract delta to
refine the individual contract in A. Similarly, the delta can
specify a contract delta that refines the default contract in A. We
give a more detailed and formal description of profile refinement
in [].
Figure: The interface of a name server
To exemplify the notion of profile definition, consider the interface of a name server in Figure 14 . The profile called nameServerProfile
is a profile for the NameServer interface; it associates various contracts with the operations defined with the NameServer
interface. The nameServerProfile associates the nameServerReliability contract (introduced in Figure 11 ) as the default contract, and it associates a refinement of the nameServerReliability contract with the lookup operation.
Notice that the contract for the lookup operation must refine the default contract (in this case, the default contract is nameServerReliability ). Since the contract for operations must always refine the default contract, it is implicitly understood that the contract expression in an operation contract is in fact a refinement.
There are many ways in which QoS profiles can be bound to specific services. They can be negotiated and associated with deals between clients and server, or they can be associated statically at design or deployment time. For the purpose of this paper we will provide an example binding mechanism that allows clients to statically bind profiles to references. In addition, we allow a server to state the profile of its implementation. These bindings could be used to ensure compatible characteristics for clients and servers as well as runtime monitoring. An abstract syntax for our notion of binding is illustrated in Figure 16 .
Figure: Abstract syntax for bindings
Figure 17 illustrates our notion of binding. In the first example the client declares a reference called myNameServer as a reference to a name server. The client's QoS requirements are expressed by means of the profile called nameServerProfile . In the second example, the implementation called myNameServerImp is declared to implement the service specification that consists of the interface called NameServer
and the profile called nameServerProfile .
The binding mechanism need not be a part of QML but has been included here for clarity. Bindings are more closely related to interface specification, design and implementation languages. As an example we will propose a binding mechanism for UML in section 5.
We define a conformance relation on profiles, contracts, and constraints. A stronger specification conforms to a weaker specification. We need conformance at runtime so that client-server connections do not have to be based on exact match of QoS requirements with QoS properties. Instead of exact match, we want to allow a service to provide more than what is required by a client. Thus, we want service specifications to conform to client specifications rather than match them exactly.
Profile conformance is defined in terms of contract conformance. Essentially, a profile P conforms to another profile Q if the contracts in P associated with an entity e conform to the contracts associated with e in the profile Q.
Contract conformance is in turn defined in terms of conformance for constraints. Constraint conformance defines when one constraint in a contract can be considered stronger, or as strong as, another constraint for the same dimension in another contract of the same contract type.
To determine constraint conformance for set dimensions, we need to determine whether one subset conforms to another subset. Conformance between two subsets depends on their ordering. In some cases, a subset represents a stronger commitment than its supersets. As an example, let us consider the failure-masking dimension. If a value of a failure-masking dimension defines the failures exposed by a server, a subset is a stronger commitment than its supersets (the fewer failure types exposed, the better). If, on the other hand, we consider a payment protocol dimension for which sets represent payment protocols supported by a server, a superset is obviously a stronger commitment than any of its subsets (the more protocols supported, the better). Thus, to be able to compare contracts of the same type the dimension declarations need to define whether subsets or supersets are stronger.
A similar discussion applies to the numeric domain. Sometimes, larger numeric values are considered conceptually stronger than smaller. As an example, think of throughput. For dimensions such as latency, smaller numbers represent stronger commitments than larger numbers.
In general, we need to specify whether smaller domain elements are
stronger than or weaker than larger domain elements. The
declaration implies that smaller elements are
stronger than larger elements. The 
declaration means
that larger elements are stronger than smaller elements.
If a dimension is declared as decreasing, we map ``stronger than'' to
``less than'' (<). Thus, a value is stronger than another value, if it
is smaller. An increasing dimension maps ``stronger than'' to
``greater than'' 
. The semantics will be that larger values are,
considered stronger.
We want conformance to correspond to constraint satisfaction. For
example, we want the constraint d < 10 to conform to the constraint
d < 20. But d < 10 only conforms to d < 20 if the domain is
decreasing (smaller values are stronger). To achieve the property that
conformance corresponds to constraint satisfaction, we allow only
the operators 
for decreasing domains, and we allow
only the operators 
for increasing domains. Thus, if we
have an increasing domain, the constraint d < 20 would be illegal.
If a profile Q is a refinement of another profile P, Q will also conform to P. Refinement is a static operation that gives a convenient way to write QoS specifications in an incremental manner. Conformance is a dynamic operation that, at runtime, can determine whether one specification is stronger than another specification. For more details on conformance we refer to [].
