

Suppose a disk track contains n sectors, its free space percentage is p, and the free space is randomly distributed. Section 2.1 gives the average number of sectors the disk head must skip before arriving at a free sector:

Proof.
Suppose k is the number of free sectors in
the track and E(n,k) is the expected number of used sectors we
encounter before reaching the first free sector. With a probability
of k/n, the first sector is free and the number of sectors the disk
head must skip is 0. Otherwise, with a probability of (n-k)/n, the
first sector is used and we must continue searching in the remaining
(n-1) sectors,
of which k are free. Therefore, the expected delay in this case is
[1 + E(n-1,k)]. This yields the recurrence:
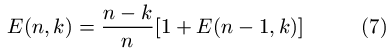
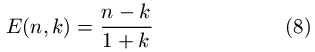
Formula (6) models the latency to locate a single sector (or a block). To extend it to situations where we need to find multiple disk sectors (or blocks) to satisfy a single file system block allocation, consider the two following examples. First, let us suppose that the host file system writes 4 KB blocks. If the disk allocates and frees 512 B sectors, it may need to locate eight separate free sectors to complete eager writing one logical block. If the disk uses a physical block size of 4 KB instead, although it takes longer to locate the first free 4 KB-aligned sector, it is guaranteed to have eight consecutive free sectors afterwards. In general, suppose the file system logical block size is B and the disk physical block size is b (b<=B), then the average amount of time (expressed in the numbers of sectors skipped) needed to locate all the free sectors for a logical block is:

Formula (9) indicates that the latency is lowest when the physical block size matches the logical block size.