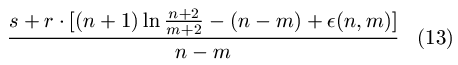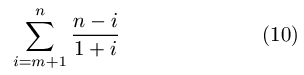
We derive the model of Section 2.3. If writes arrive with no delay, then it would be trivial to fill the track. If writes arrive randomly and we assume the free space distribution is random at the time of the arrivals, then writes between successive track switches follow the model of (6). Therefore, substituting pn in (6) with i, the number of free sectors, the total number of sectors to skip between track switches can be expressed as:
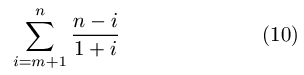
where n is the total number of sectors in a track and m is the number of free sectors reserved per track before switching tracks. Suppose each track switch costs s and the rotation delay of one sector is r; because we pay one track switch cost per (n-m) writes, the average latency per sector of this strategy can be expressed as:
So far, we have assumed that the free space distribution is always
random.
This is not the case with the approach of filling the track
up to a threshold because, for example, the first free sector
immediately following a number of used sectors is more likely to be
selected for eager writing than one following a number of free
sectors. In general, this non-randomness increases latency. Although
the precise modeling of the non-randomness is quite complex, through
approximations and empirical trials, we have found that adding the
following 
function to (10) works well
for a wide range of disk parameters in practice:
where p = 1 + n/36. By approximating the summation in (10) with an integral and adding the correction factor of (12) to account for the non-randomness, we arrive at the final latency model:
